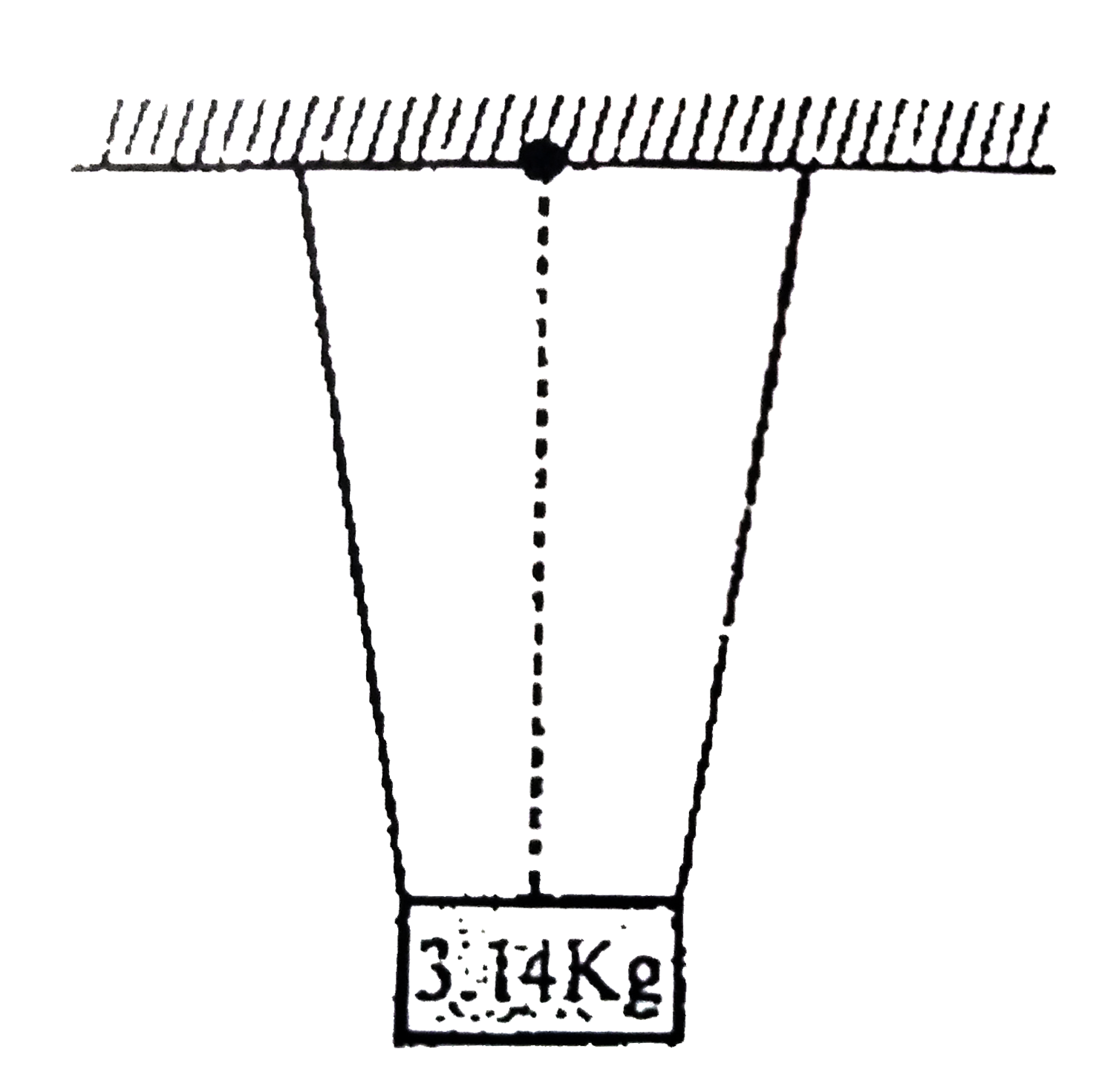
A body of mass 3.14kg is suspended from one end of a wire of length 10m. The radius of cross-section of the wire is changing uniformly from 5×10−4m at the top (i.e. point of suspension) to 9.8×10−4m at the bottom . Young's modulus of elasticity is 2×1011N/m2. The change in length of the wire is
4×10−3m
3×10−3m
10−3m
2×10−3m
The correct Answer is:C
Change in length of element is
Cross-sectional area of the element is
A=π[a+b−aLx]2
Where , a=b−aLx is radius of the wire at the location of element .
d(Δl)=Fπ[a+b−aLx]2Ydx
Total change in length of wire is
Δl=FπY∫Lo1(a+b−aLx)2dx
Let a+b−aLx=t
⇒b−aLdx=dt⇒dx=Lb−adt
When x=o , t=a and when x=L,t=b
∴Δl=FπY∫bat−2.Lb−adt
=FLπY(b−a)(−1)(1b−1a)
=FLπY(b−a).b−aab=FLπYab
=(3.14)(9.8)(10)(3.14)(2×1011)(5×10−4)(9.8×10−4)
=10−3m⇒∴ΔL=10−3m

Topper's Solved these Questions
- ELASTICITYBOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Level 1 Subjective
8 Videos
- ELASTICITYBOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Level 2 Single Correct
10 Videos
- ELASTICITYBOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Assertion And Reason
22 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
434 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
Similar Questions
A body of mass 3.14 kg is suspended from one end of a non uniform wire of length 10m, such that the radius of the wire is changing uniformly from 9.8×10−4 m at one end to 5×10−4 m at the other end. Find the change in length of the wire in mm. Young's modulus of the material of the wire is 2×1011N/m2 (mass of wire is negligible)
View SolutionA steel wire of length 3.0m is stretched through 3.0 mm. the cross-sectional area of the wire is 5.0mm2. Calculate the elastic potential energy stroed in the wire in the stretched condition. Young's modulus of steel is 2.0×1011Nm−2.
View Solution
Knowledge Check
A body of mass 6.28 kg is suspended from one end of a wire of length 10 m. The radius of the wire is changing uniformly from 19.6×10−4m at one end to 10×10−4m at the order end. Find the change in the length of the wire.
[Y=2×1011N/m2]A0.1 mmB0.3 mmC0.5 mmD0.7 mmA wire of area of cross section 1×10−6m2 and length 2 m is stretched through 0.1×10−3m. If the Young's modulus of a wire is 2×1011N/m2, then the work done to stretch the wire will be
A0.05×10−4JB0.5×10−4JC5×10−4JD50×10−4JAn iron wire of length 4 m and diameter 2 mm is loaded with a weight of 8 kg. if the Young's modulus Y for iron is 2×1011N/m2 then the increase in the length of the wire is
A0.2 mmB0.5 mmC2 mmD1 mm
A block of mass M is suspended from a wire of length L, area of cross-section A and Young's modulus Y. The elastic potential energy stored in the wire is
View SolutionA copper wire of length 4.0mm and area of cross-section 1.2cm2 is stretched with a force of 4.8×103N. If Young's modulus for copper is 1.2×1011N/m2, the increases in the length of the wire will be
View SolutionA wire of density 9×103kg/m3 is stretched between two clamps 1 m apart and is stretched to an extension of 4.9×10−4 metre.Young's modulus of material is 9×1010N/m2.Then
View SolutionA wire of density 9×103kg/m3 is stretched between two clamps 1 m apart and is stretched to an extension of 4.9×10−4 metre.Young's modulus of material is 9×1010N/m2.Then
View SolutionA steal wire of cross-section area 3×10−6m2 can withstand a maximum strain of 10−3 .Young's modulus of steel is 2×1011Nm−2 .The maximum mass this wire can hold is
View Solution
