A body of mass m falls from a height h on to the pan of a spring balance, figure, The masses of the pan and spring are negligible. The spring constant of the spring is k. The body gets attached to the pan and starts executing S.H.M. in the vertical direction. Find the amplitude and energy of oscillation.
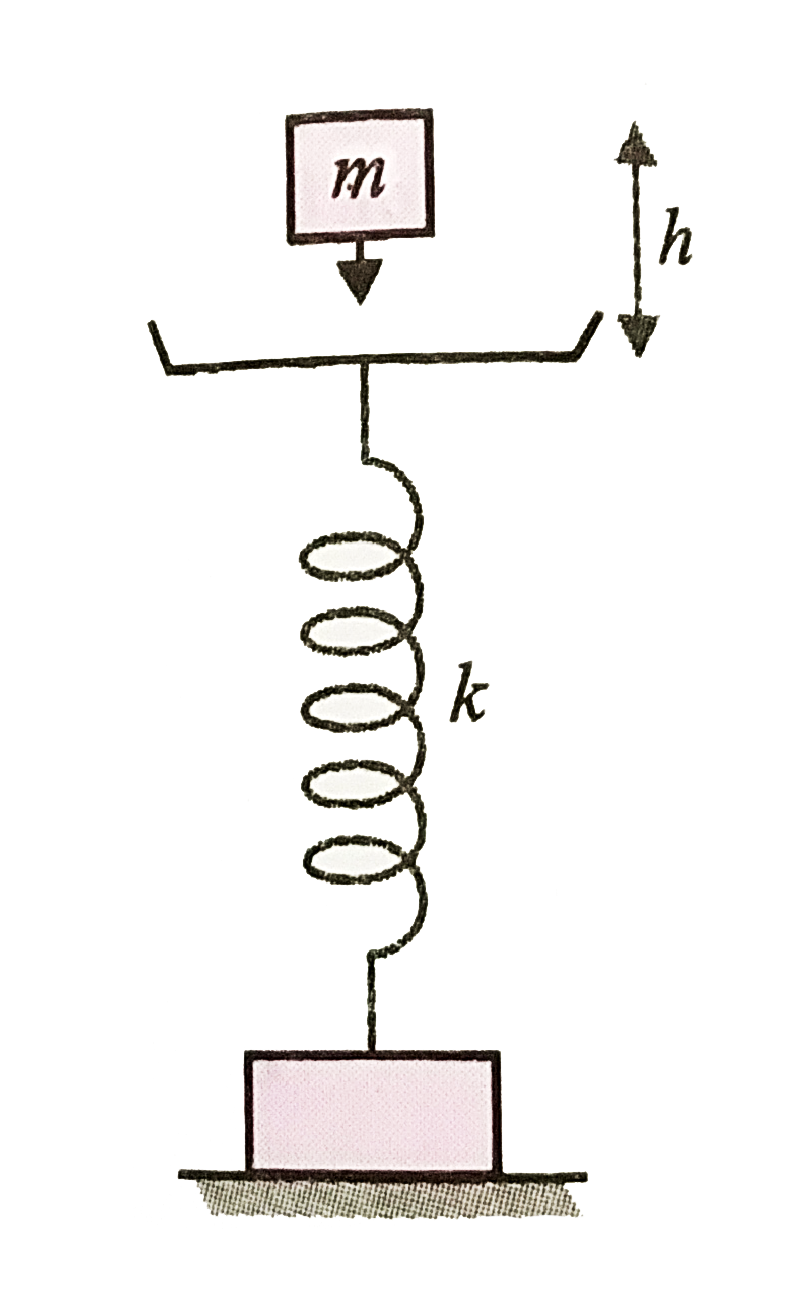
The correct Answer is:a=mgk√1+2kh(M+m)g,T=2π√(M+m)/k
Step by step video, text & image solution for A body of mass m falls from a height h on to the pan of a spring balance, figure, The masses of the pan and spring are negligible. The spring constant of the spring is k. The body gets attached to the pan and starts executing S.H.M. in the vertical direction. Find the amplitude and energy of oscillation. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - NN GHOSHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Eexercies
39 Videos
- SIMPLE AND COMPOUND PENDULUMBOOK - NN GHOSHCHAPTER - SIMPLE AND COMPOUND PENDULUMEXERCISE - Exercise
24 Videos
- SPECIFIC HEAT CAPACITY OF GASESBOOK - NN GHOSHCHAPTER - SPECIFIC HEAT CAPACITY OF GASESEXERCISE - All Questions
17 Videos
Similar Questions
A body of mass m falls from a height h on to the pan of a spring balance. The masses of the pan and spring are negligible. The spring constant of the spring is k. Having stuck to the pan the body starts performing harmonic oscillations in the vertical direction. Find the amplitude and energy of oscillation.
View SolutionA load of mass m falls from a height h on to the scale pan hung from a spring , as shown in the figure . If the spring constant is k , mass of the not bounce , relative to the pan , then the amplitude of vibration is
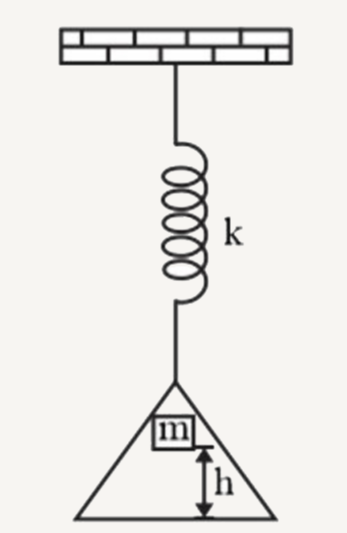
View Solution
Knowledge Check
A body of mass m falls from a height h onto the pan of a spring balance. The masses of the pan and spring are negligible. The force constant of the spring is k. The body sticks to the pan and oscillates simple harmonically. The amplitude of oscillation is
 AmgkBmgk√1+2hkmgCmgk(1+√1+2hkmg)Dmgk√1+(2hkmg)−1
AmgkBmgk√1+2hkmgCmgk(1+√1+2hkmg)Dmgk√1+(2hkmg)−1A body of mass m falls from a height h on a pan ( of negligible mass ) of spring balance as shwon. The spring is ideal and has a spring contant k. Just after striking the pan, the body sticks with the pan and starts oscillatory motion in vertical direction. The velocity of the body at mean position will be
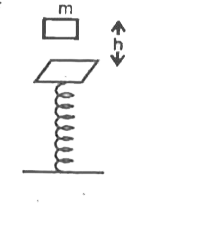 A√2mg2k+2ghB√k2ghmC√mg2k+2ghD√mg2k+4gh
A√2mg2k+2ghB√k2ghmC√mg2k+2ghD√mg2k+4ghA load of mass m falls from a height h on to the scale pan hung from a spring as shown in the adjoining figure. If the spring constant is k and mass of the scale pan is zero and the mass m does not bounce relative to the pan, then the amplitude of vibration is
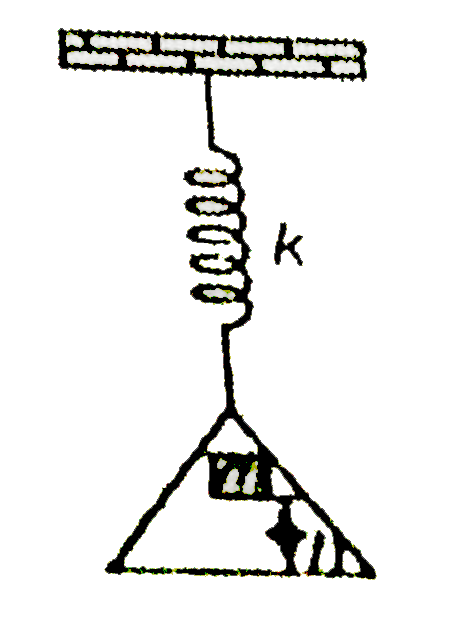 AmgkBmgk√(1+2hkmg)Cmgk+mgk√(1+2hkmg)Dmgk√(1+2hkmg−mgk)
AmgkBmgk√(1+2hkmg)Cmgk+mgk√(1+2hkmg)Dmgk√(1+2hkmg−mgk)
A load of mass m falls from a height h on to the scale pan hung from a spring , as shown in the figure . If the spring constant is k , mass of the not bounce , relative to the pan , then the amplitude of vibration is

View SolutionFor a body of mass m attached to the spring the spring factor is given by
View SolutionA body of mass m is released from a height h to a scale pan hung from a spring. The spring constant of the spring is k, the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is
View SolutionA body of mass m falls from a height h onto the pan of a spring balance. The masses of the pan and spring are negligible. The force constant of the spring is k. The body sticks to the pan and oscillates simple harmonically. The amplitude of oscillation is

View SolutionA body is kept in the pan of a spring balance kept in an elevator. The reading of the spring scale will be maximum when the elevator
View Solution