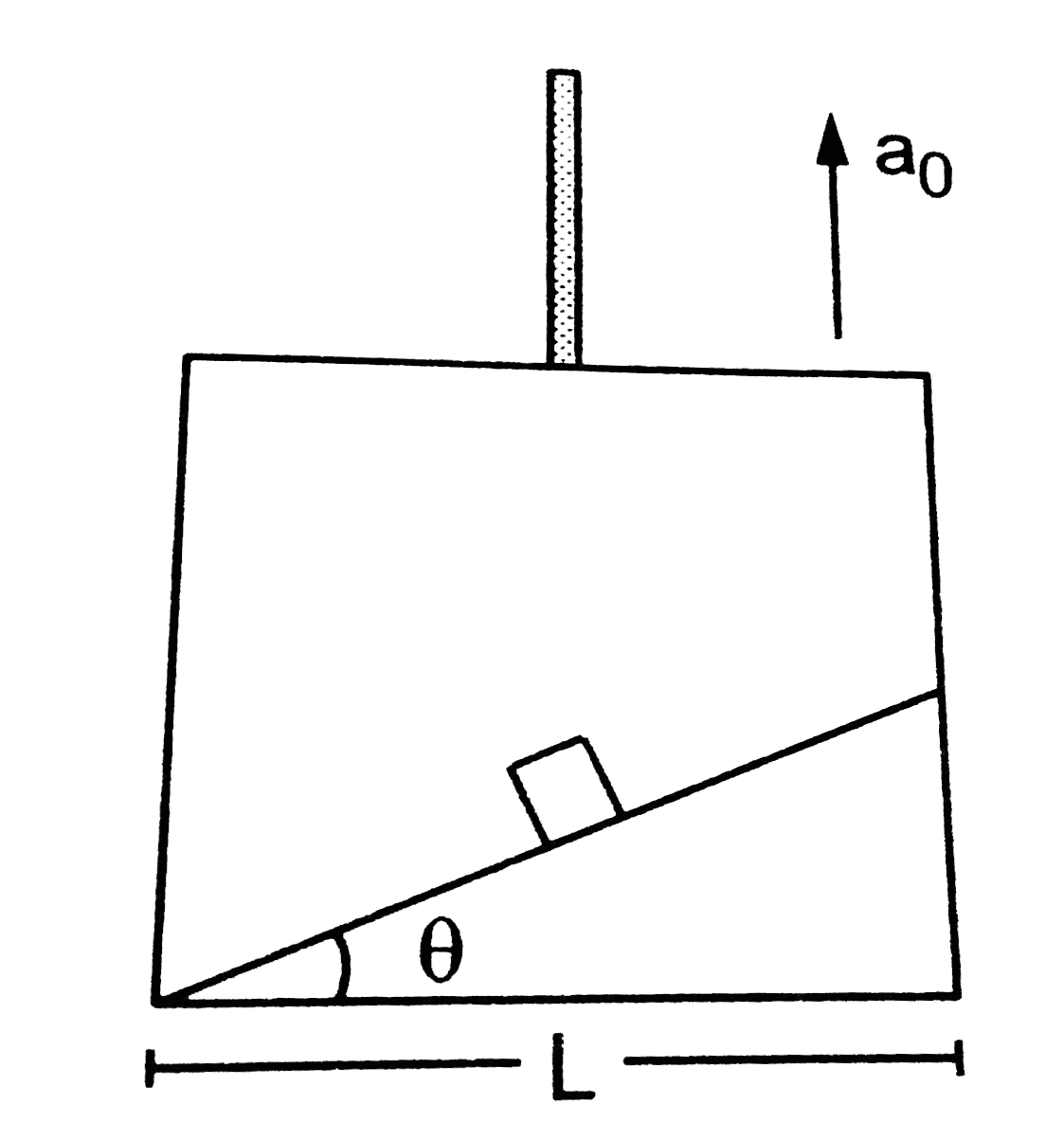
A body of mass m is placed over a smooth inclined plane of inclination theta. Which iis placed over a lift which is moving up with an acceleration a0 . Base length o f the inclined plane is L . Calculate the velocity of the block with respect to lift at the bottom, if it is allowed to slide down from the top o fthe plane from rest.
√2(a0+g)Lsinθ
√2(a0+g)Lcosθ
√2(a0+g)Ltanθ
√2(a0+g)Lcotθ
The correct Answer is:C
Acceleration along the plane with respect to lift is,
a=(a0+g)sinθ
Initial velocity=0
v2=u2+2as
v=√2(a0+g)sinθlcosθ .
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Basic Concept Of Static And Kinetic Frictions
45 Videos
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Dynamics Of Circular Motion
31 Videos
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Equilibrium Of A Particle
19 Videos
- MOTION IN TWO DIMENSIONBOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Chapter Test
29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test
29 Videos
Similar Questions
A particle slides down a smooth inclined plane of elevation θ fixed in a elevator going up with an acceleration a0. The base of the inline has a length L.
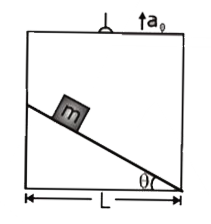
View SolutionA particle slides down a smooth in clined plane of elevation θ fixed in an elevastor going up with an accelerationa0. The base of the incline has a length L.Find the time taken by the particle to reach the bottom.
View Solution
Knowledge Check
A body of mass m is placed over a smooth inclined plane of inclination θ, which is placed over a lift which is moving up with an acceleration a0 . Base length of the inclined plane is L. Calculate the velocity of the block with respect to lift at the bottom, if it is allowed to slide down from the top of the plane from rest :-
A√2(a0+g)LsinθB√2(a0+g)LcosθC√2(a0+g)LtanθD√2(a0+g)LcotθA block can slide on a smooth inclined plane of inclination θ kept on the floor of a lift. When the lift is descending with a retardation a , the acceleration of the block relative to the incline is
AThe acceleration of block relative to inclined is (g−a)sinθBThe normal force on block by the incline is m(g+a)cosθCThe acceleration of block relative to ground is gDThe acceleration of block relative to incline is (g+a)sinθA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
AmgBmgcosθCmgcosθDmgtanθ
A frictionless inclined plane of length l having inclination θ is placed inside a lift which is accelerating downward with on acceleration a (<g). If a block is allowed to move down the inclined plane, from rest, then the time taken by the block to slide from top of the inclined plane to the bottom of the inclined plane is
View SolutionA block is placed on an inclined plane moving towards right with an acceleration a0=g The length of the inclined plane is l0. All the surfaces are smooth Find the time taken by the block to reach from bottom to top.
 .
.
View SolutionA block can slide on a smooth inclined plane of inclination θ kept on the floor of a lift. When the lift is descending with a retardation a , the acceleration of the block relative to the incline is
View SolutionA block is released from rest on a smooth inclined plane having inclination 37∘ with the horizontal. The inclined plane is fixed on a lift which is moving up with retardation 5ms−2. Find out the displacement of the block with respect to the lift in initial 1 second (Take g=10ms−2)

View SolutionA body is released from the top of a smooth inclined plane of inclination θ. It reaches the bottom with velocity v. If the angle of inclination is doubled for the same length of the plane, what will be the velocity of the body on reaching the ground
View Solution
