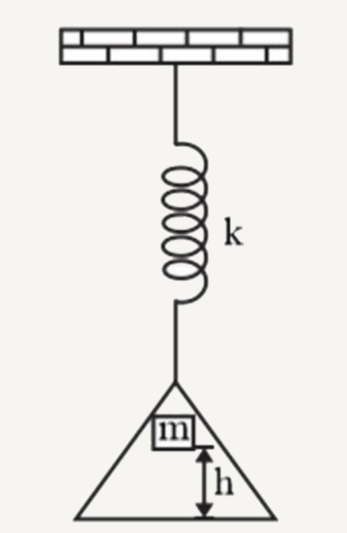
A body of mass m is released from a height h to a scale pan hung from a spring. The spring constant of the spring is k, the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is
As the pan is of negligible mass, there is no loss of kinetic energy even though the collision is inelastic. The meachanical energy of the body m in the fiels generated by the joing action of both the gravity force and the elastic force is conserved i.e.,ΔE=0. During the motion of the body m from the initial to the final ( positon of maxiumu compression of the spring) position ΔT=0, and thereforeΔU=ΔUgr+ΔUsp=0
or −mg(h+x)+12kx2=0
On solving the quadratic equation :
x=mgk±√m2g2k2+2mghk
As minus sign is not acceptable
x=mgk+√m2g2k2+2mghk
If the body m were at rest on the spring, the corresponding position of m will be its equilibrium position and at this position the resultant force on the body m will be zero. Therefore the equilibrium compression Δx (say ) due to the body m will be given by
kΔx=mg or Δx=mg/k
Therefore separation betweent the equilibrium position and one of the extremen position i.e. the sought amplitude lt brgt a=x−Δx+√m2g2k2+2mghk
The mechanical energy of oscillation which is conserved equals E=Uextreme, because at the extreme position kinetic energy becomes zero .
Althought the weight of body m is a conservative force, it is not restoring in this problem, hence Uextreme is only concerned with the spring force. Therefore
E=Uextreme=12ka2=mgh+m2g22k
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electric Oscillations
56 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
A load of mass m falls from a height h on to the scale pan hung from a spring , as shown in the figure . If the spring constant is k , mass of the not bounce , relative to the pan , then the amplitude of vibration is
View Solution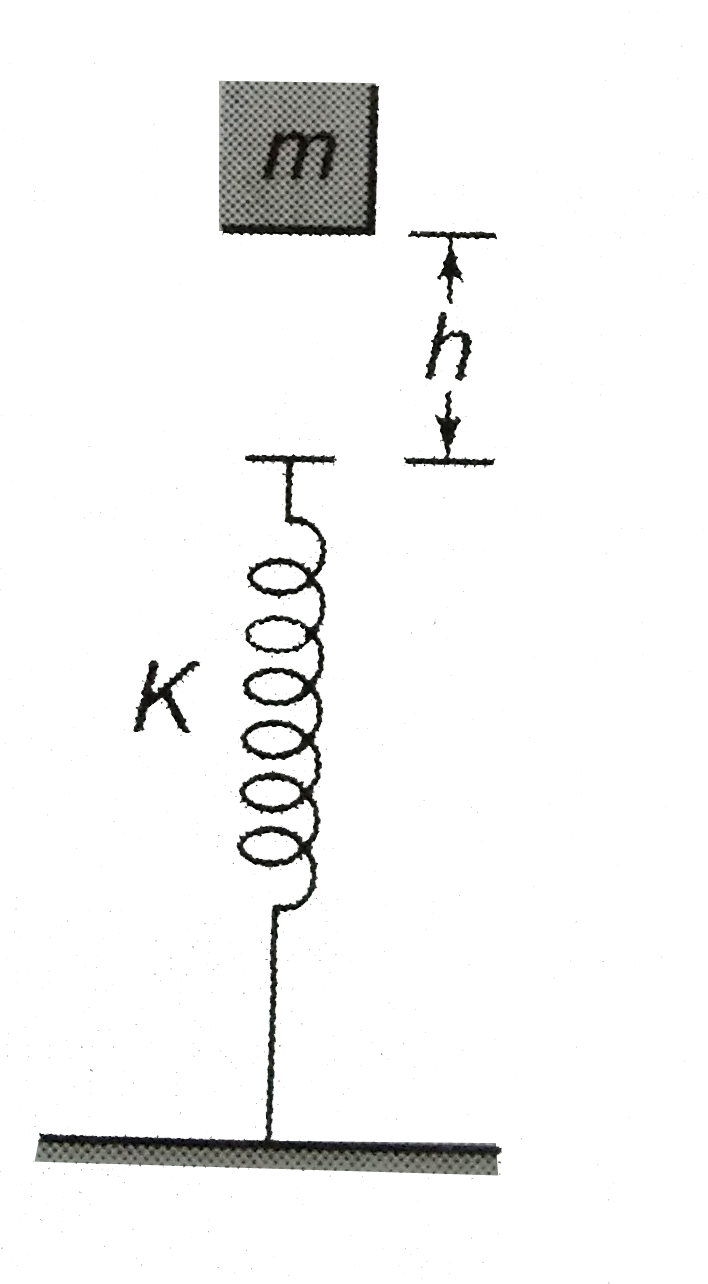
A block is released from height h, find the maximum compression of spring of spring constant k.
View Solution
Knowledge Check
A body of mass m falls from a height h onto the pan of a spring balance. The masses of the pan and spring are negligible. The force constant of the spring is k. The body sticks to the pan and oscillates simple harmonically. The amplitude of oscillation is
 AmgkBmgk√1+2hkmgCmgk+mgk√1+2hkmgDNone of these
AmgkBmgk√1+2hkmgCmgk+mgk√1+2hkmgDNone of theseA load of mass m falls from a height h on to the scale pan hung from a spring , as shown in the figure . If the spring constant is k , mass of the not bounce , relative to the pan , then the amplitude of vibration is
 Amg/dBmgk√(1+2hkmg)Cmgk+mgk√(1+2hkmg)Dmgk√(1+2hkMg−mgk)
Amg/dBmgk√(1+2hkmg)Cmgk+mgk√(1+2hkmg)Dmgk√(1+2hkMg−mgk)A load of mass m falls from a height h on to the scale pan hung from a spring as shown in the adjoining figure. If the spring constant is k and mass of the scale pan is zero and the mass m does not bounce relative to the pan, then the amplitude of vibration is
 AmgkBmgk√(1+2hkmg)Cmgk+mgk√(1+2hkmg)Dmgk√(1+2hkmg−mgk)
AmgkBmgk√(1+2hkmg)Cmgk+mgk√(1+2hkmg)Dmgk√(1+2hkmg−mgk)
A body of mass m falls from a height h on to the pan of a spring balance. The masses of the pan and spring are negligible. The spring constant of the spring is k. Having stuck to the pan the body starts performing harmonic oscillations in the vertical direction. Find the amplitude and energy of oscillation.
View SolutionA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View Solution
A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x then
View SolutionA body of mass m falls from a height h onto the pan of a spring balance. The masses of the pan and spring are negligible. The force constant of the spring is k. The body sticks to the pan and oscillates simple harmonically. The amplitude of oscillation is

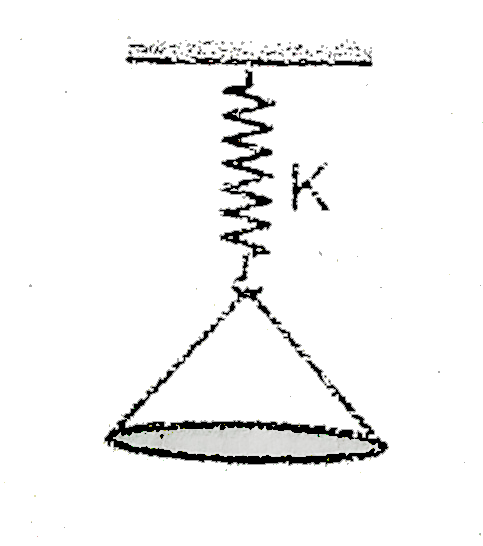
View SolutionA solid ball of mass m is made to fail from a height H on a pan suspended through a spring of spring constant K as shown in figure. If the does not rebound and the pan is massless, then amplitude of oscillation is
View Solution
