A bowl with a semi spherical base is designed such that its centre of gravity is located at the centre of curvature of the spherical part. Explain giving reasons, to which state of equilibrium the bowl belongs. If the bowl is filled with water upto the centre of gravity, explain how the equilibrium state would be affccted/unaffccted.
Step by step video & image solution for A bowl with a semi spherical base is designed such that its centre of gravity is located at the centre of curvature of the spherical part. Explain giving reasons, to which state of equilibrium the bowl belongs. If the bowl is filled with water upto the centre of gravity, explain how the equilibrium state would be affccted/unaffccted. by Physics experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GRAVITATIONBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GRAVITATIONEXERCISE - ESSAY TYPE QUESTIONS
5 Videos
- GRAVITATIONBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GRAVITATIONEXERCISE - LEVEL-1
44 Videos
- GRAVITATIONBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GRAVITATIONEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
30 Videos
- ElectricityBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - ElectricityEXERCISE - Level 3
10 Videos
- HEATBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - HEATEXERCISE - All Questions
115 Videos
Similar Questions
Knowledge Check
A fish is near the centre of a spherical water filled(μ=4/3)fish bowl,A child stands in air ata distance 2R(Ris the radius of curvature of the sphere)from the centre of the bowl.At what distance from the centre would the child nose appear to the fish situated at the centrer:
A4RB2RC3RD4RAssertion : For a floating body to be in stable equilibrium, its centre of buoyancy must be located above the centre of gravity.
Reason : The torque produced by the weight of the body and the upthrust will restore body back to its normal position, after the body is disturbed.AIf both assertion and reason are true and the reason is the correct explanation of the assertion.BIf both assertion and reason are true and the reason is not the correct explanation of the assertion.CIf assertion ture but reason is false.DIf the assertion and reason both are false.After the faliure of Bohr atomic theory but its ability to explain to the atomic spectral a need was felt for the new model that could incorporate, the concept of stationary orbit, de Broglie concept, Heisenberg uncertainity principle. The concept that in corporate above facts is called quantum mechanics of the atomic model wave mchanical model. it includes set of quantum number and ∣∣ψ2∣∣ a mathematical expression of the probability of finding an electron at all points in space. This probability function is the best indication available of how the electon behaves, for as a consequence of the Uncertainity Principle, the amount we can know about the electron is limited. While quantum mechanics can tell us the exact probability of finding an electron at any two particular points, it does not tell us how the electron moves from one of these points to the other. Thus the idea of an electron orbit is lost, it is replaced with a description of where the electron is most likely to be found. This total picture of the probability of finding an electron at various points in space is called an orbital.
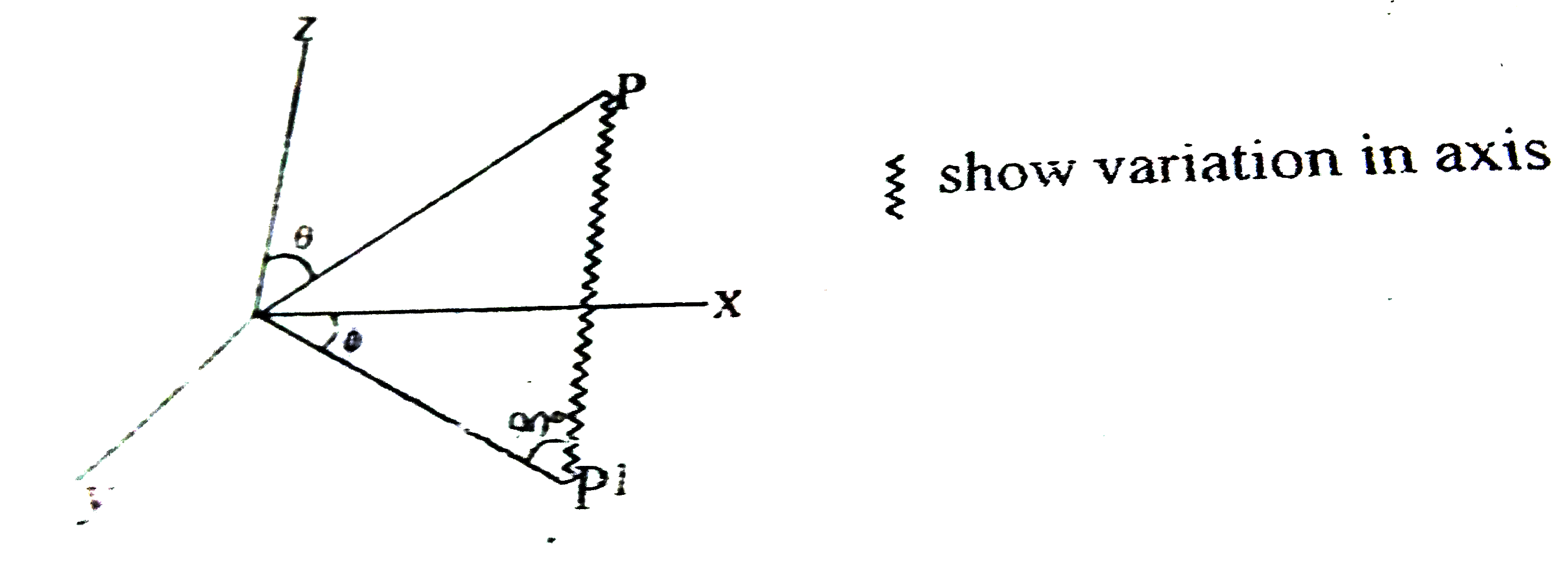
There are various types of orbitals possible, each corresponding to one of the possible combinations of quantum numbers. These orbitals are classified according to the value of n and l associated with them. In order to avoid confusion over the use of two numbers, the numerical velues of l are replaced by letters, electrons in orbitals with l=0 are called s-electrons those occupying orbitals for which l=1 are p-electrons and those for which l=2 are called d-electrons. The numerical and alphabetical correspondences are summarized in table. Using the alphabetical notation for l, we would say that in the ground state of hydrogen atom (n=1,l=0) we have a 1s-electron, or that the electron moves in a 1s-orbital. The relation of the spherical polar co-ordinates r,θ and ϕ to Cartesian coordinates x, y and z. To make the concept of an orbital more meaningful, it is helpful to examine the actual solution of the wave function for the one-electron atom. Because of the spherical sysmmetry of the atom, the wave functions are most simply expressed in terms of a spherical polar-coordinate system, shown in fig., which has its orbit at the nucleus. It is found that the wave function can be expressed as the product of two functions, one of which (the ''angular part'' X) depends only the angle θ and ϕ the other of which (the ''radial part'' R) depends only on the distance from the nucleus. Thus we have
ϕ(r,θ,ϕ)=R(r)X(θ,ϕ)
Angular and radial parts of hydrogen atom wave function
(Angular partX(θ,ϕ),,Radial partRn,l(r)),(X(s)=(14π)1/2,,R(1s)=2(za0)3/2e−σ/2),(X(px)=(34π)1/2sinθcosϕ,,R(2s)=12√2(za0)3/2(2−σ)e−σ/2),(X(py)=(34π)1/2sinθsinϕ,,R(2p)=12√6(za0)3/2σe−σ/2),(X(pz)=(34π)1/2cosθ,,),(X(d22)=(516π)1/2(3cos2θ−1),,),(X(dxz)=(154π)1/2sinθcosθcosϕ,,R(3s)=19√3(za0)3/2(6−6σ+σ2)e−σ/2),(X(dyz)=(154π)1/2sinθcosθsinϕ,,R(3p)=19√6(za0)3/2(4−σ)σe−σ/2),(X(dx2−y2)=(154π)1/2sin2θcos2ϕ,,R(3d)=19√30(za0)3/2σ2e−σ/2),(X(dxy)=(154π)1/2sin2θsin2ϕ,,),(,,σ=2Zrna0,a0=h24π2me2)
This factrorization helps us to visualize the wave function, since it allows us to consider the angular and radial dependences separately. It contains the expression for the angular and radial parts of the one electron atom wave function. Note that the angular part of the wave function for an s-orbital it alwats the same, (1/4π)1/2 regardless of principal quantum number. It is also true that the angular dependence of the p-orbitals and of the d-orbitals is independent of principle quantum number. Thus all orbitals of given types (s, p, or d) have the same angular behavour The table shows, however, that the radial part of the wave function depends both on the principal quantum n and on the angular momentum quantum number l.
To find the wave function for a particular state, we simply multiply the appropriate angular and radial parts togather called normalized wave function.
The probability of finding an electron at a point within an atom is proportional to the square of orbital wave function, i.e., ψ2 at that point. Thus, ψ2 is known as probability density and always a positive quantity.
ψ2dV(orψ2.4πr2dr). represents the probability for finding electron in a small volume dV surrounding the nucleus.
The angular wave function of which orbital with not disturb by the variation with azimuthal angle onlyA1s and 2sB2pz and 2d2zC2px and 3d2zD2px and 2s
A spherical fish bowl of radius R is placed in front of a plane vertical mirror (M) The thickness of the wall of the fish bowl is very thin The centre (C) of the spherical bowl is at distance of 3R from the plane mirror. The bowl is filled with water and contains a fish (F) Fish(F) is at a distance of R from the centre of the spherical bowl as shown in the figure Refractive index of water is 4/3 two surfaces are indicated in the bowl as first surface (1) and second surface(2)

{:(,"Column-I",,"Column-II"),(,ul("Optical Event"),,ul("Nature of image")),(,"(A)Refraction at first surface",,"(P)Virtual"),(,"(B)Refraction at second surface after reflection from mirror",,"(Q)Real"),(,underset("from mirror and refraction from second surface")"(C)Refraction at first surface after reflection",,"(R)Magnified"),(,,,"(S)Diminished"):}
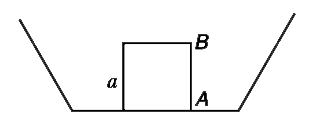
View Solution(i) A non uniform cube of side length a is kept inside a container as shown in the figure. The average density of the material of the cube is 2 ρ where ρ is the density of water. Water is gradually fille din the container. It is observed that the cube begins to topple, about its edge into the plane of the figure passing through pointA, when the height of the water in the container becomes a2. Find the distance of the centre of mass of the cube from the face AB of the cube. Assume that water seeps under the cube.
(ii) A rectangular concrete block (specific gravity =2.5) is used as a retatining wall in a reservoir of water. The height and width of the block are x and y respectively the height of water in the reservoir is z=34x. the concrete block cannot slide on the horizontal base but can rotate about an axis perpendicular to the plane of the figure and passing through point A
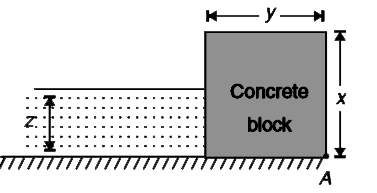
(a) Calculate the minimum value of the ratio yx for which the block will not begin to overturn about A.
(b) Redo the above problem for the case when there is a seepage and a thin film of water is present under the block. Assume that a seal at A prevents the water from flowing out underneath the block.
View SolutionA spherical shaped fish bowl filled with water of refractive index 1.3 is placed in another large tank filled with another liquid of refractive index 1.4 such that rim of the fish bowl is slightly above the liquid filled in the tank. The diameter of the fish bowl is 20 cm. A parallel light rays from a distant object is incident on the spherical fish bowl. Find the position at which incident light rays will get focused when seen by a small fish at the centre of the bowl.
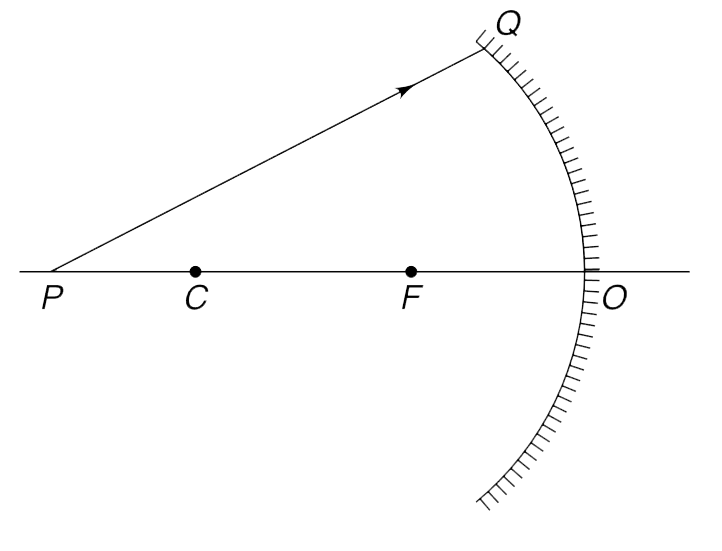
View SolutionWe know that parallel light rays which are inclined to the principal axis of a spherical mirror, after reflection converge at a point in the focal plane of the mirror. With this knowledge explain how you will trace the reflected ray for incident ray PQ shown in the Fig. F is focus and C is centre of curvature of the mirror.
View SolutionA beaker of radius r is filled with water (refractive index 43) up to a height H as shown in the figure on the left. The beaker is kept on a horizontal table rotating with angular speed ω. This makes the water surface curved so that the difference in the height of water level at the centre and the circumference of the beaker is h (h<<H,h<<r) as shown in the figure on the right . Take this surface to be approximately spherical with a radius of curvalture R . Which of the following is/are correct ? (g is acceleration due to gravity)
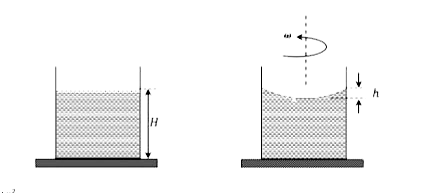
View Solution

