A boy is standing on a weighing machine placed on the floor of an elevator. The elevator starts going down with some acceleration, moves with constant velocity for some time and finally decelerates to stop. The minimum and maximum weight recorded are 480N and 840N If the magnitude of reardation is double of acceleration, find (a) true weight of the boy and (b) magnitude of acceleration.
(A) When the elevator is under acceleration

mg−N0=ma=ma0
N0=m(g−a0)=Wmin480
(b) When the wlevator is under retardation
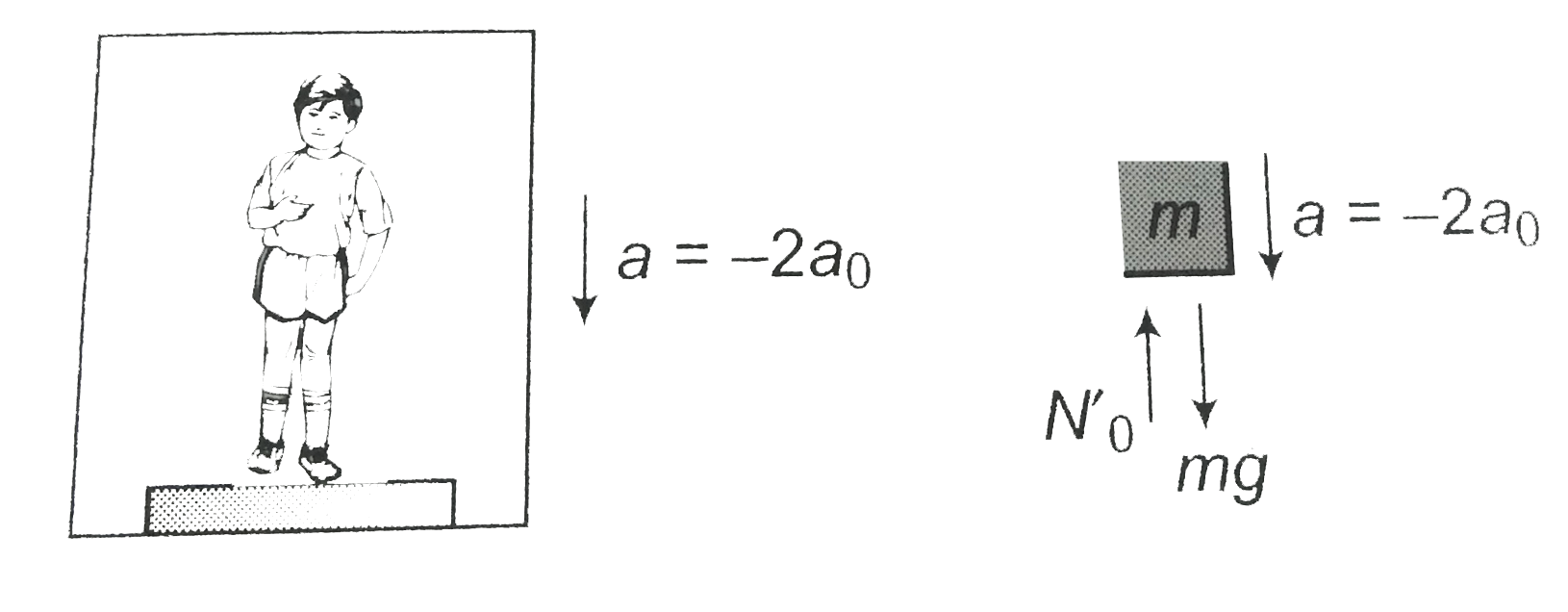
mg−N0'=m(−2a0)
N0'=m(g+3a0)=Wmax=840 (ii)
Dividing (ii) by (i), we get
m(g+a0)m(g+a0)=840480⇒g+3a0g+a0=74
⇒a0=0.6g=6m/s2
m(g+a0)=480
m(10+6)=480⇒m=30kg
True weight of the boy =mg=30×10=300N
Magnitude of acceleration 6m/s2
Topper's Solved these Questions
Similar Questions
A perso is standing on a weighing machine placed on the floor of an elevator. The elevator starts going up with some acceleratiion, moves with uniform velocity for a while and finally decelerates to stop. The maximum and the minimum weights recorded are 72 kg and 60 kg. Assuming that the magnitudes of the acceleration and the decelaration are teh same., find a. the true weight of the person and b. the magnitude of the acceleration. Take g=9.9ms2.
 View Solution
View SolutionA man of mass 40kg is standing on a weighting machine kept on the floor of an elevator which is moving up with an acceleration of 2m/s2 Find the reading of the weighing maching.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A 60 kg boy stands on a scale in the elevator. The elevator starts moving and records 450 N. Find the acceleration of the elevator.
A2.5ms−2 upwardB2.5ms−2 downwardsC2.5ms−2 in either directionD2.0ms−2upward - Question 2 - Select One
A man is standing on a weighing machine kept on the floor of an elevator. The ratio of measured weight of the man when elevator is at rest and when it is moving with downward acceleration a is 3 : 2. The value of a is :
Ag3B3g2CgD2g3 - Question 3 - Select One
A train starts from rest and moves with uniform acceleration α for some time and acquires a velocity v it then moves with constant velocity for some time and then decelerates at rate β and finally comes to rest at the next station. If L is distance between two stations then total time of travel is
ALV+V2(1α+1β)BLV−V2(1α+1β)CLV−V2(1α−1β)DLV+V2(1α−1β)
A man of mass 40kg is standing on a weighting machine kept on the floor of an elevator which is moving up with an acceleration of 2m/s2 Find the reading of the weighing maching.
 View Solution
View SolutionA 60 kg boy stands on a scale in the elevator. The elevator starts moving and records 450 N. Find the acceleration of the elevator.
View SolutionA man is standing on a weighing machine kept on the floor of an elevator. The ratio of measured weight of the man when elevator is at rest and when it is moving with downward acceleration a is 3 : 2. The value of a is :
View SolutionA car acceleration form rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t evaluate (a) the maximum velocity attained and (b) the total distance travelled.
View SolutionA boy standing on a weighing machine notices his wight as 400 N. When he suddenly jumps upward the weight shown by the machine becomes 600 N. The acceleration with which the boy jumps up is : (Take g=10m/s2)
View Solution
