A boy of mass 60kg is standing over a platform of mass 40kg placed over a smooth horizontal surface. He throws a stone of mass 1kg with velocity v=10m/s at an angle of 45∘ with respect to the ground. Find the displacement of the platform (with boy) on the horizontal surface when the stone lands on the ground. Take g=10m/s2.
The correct Answer is:A, C
To solve the problem, we need to find the displacement of the platform (with the boy) on the horizontal surface when the stone lands on the ground. We will follow these steps:
Step 1: Calculate the Range of the Stone
The stone is thrown with a velocity v=10m/s at an angle θ=45∘. The range R of a projectile is given by the formula:
R=u2sin(2θ)g
where u is the initial velocity, g is the acceleration due to gravity, and θ is the angle of projection.
Substituting the values:
R=(10)2sin(90∘)10=100⋅110=10m
Step 2: Determine the Initial Momentum of the System
Before the stone is thrown, the system (boy + platform) is at rest. Therefore, the initial momentum of the system is:
pinitial=0
Step 3: Calculate the Final Momentum of the Stone
When the stone is thrown, it has a mass ms=1kg and a velocity vs=10m/s at 45∘. The horizontal component of the stone's velocity is:
vsx=vscos(45∘)=10⋅1√2=5√2m/s
The momentum of the stone in the horizontal direction is:
ps=msvsx=1⋅5√2=5√2kg m/s
Step 4: Apply Conservation of Momentum
By conservation of momentum, the momentum of the system after the stone is thrown must equal the initial momentum:
pinitial=pfinal
Let vp be the velocity of the platform (with the boy) after the stone is thrown. The total mass of the platform and the boy is mb+mp=60+40=100kg.
Thus, we have:
0=ps+pp⟹0=5√2+100vp
Solving for vp:
100vp=−5√2⟹vp=−5√2100=−√220m/s
Step 5: Calculate the Time of Flight of the Stone
The time of flight t for the stone can be calculated using the vertical motion:
t=2usin(θ)g=2⋅10⋅1√210=2√22=√2s
Step 6: Calculate the Displacement of the Platform
The displacement d of the platform during the time the stone is in the air is given by:
d=vp⋅t=−√220⋅√2=−220=−0.1m=−10cm
Final Answer
The displacement of the platform (with the boy) on the horizontal surface when the stone lands on the ground is:
Displacement=−0.1m (or -10 cm)
The stone is thrown with a velocity v=10m/s at an angle θ=45∘. The range R of a projectile is given by the formula:
R=u2sin(2θ)g
where u is the initial velocity, g is the acceleration due to gravity, and θ is the angle of projection.
R=(10)2sin(90∘)10=100⋅110=10m
Before the stone is thrown, the system (boy + platform) is at rest. Therefore, the initial momentum of the system is:
pinitial=0
When the stone is thrown, it has a mass ms=1kg and a velocity vs=10m/s at 45∘. The horizontal component of the stone's velocity is:
vsx=vscos(45∘)=10⋅1√2=5√2m/s
ps=msvsx=1⋅5√2=5√2kg m/s
By conservation of momentum, the momentum of the system after the stone is thrown must equal the initial momentum:
pinitial=pfinal
Let vp be the velocity of the platform (with the boy) after the stone is thrown. The total mass of the platform and the boy is mb+mp=60+40=100kg.
0=ps+pp⟹0=5√2+100vp
Solving for vp:
100vp=−5√2⟹vp=−5√2100=−√220m/s
The time of flight t for the stone can be calculated using the vertical motion:
t=2usin(θ)g=2⋅10⋅1√210=2√22=√2s
The displacement d of the platform during the time the stone is in the air is given by:
d=vp⋅t=−√220⋅√2=−220=−0.1m=−10cm
The displacement of the platform (with the boy) on the horizontal surface when the stone lands on the ground is:
Displacement=−0.1m (or -10 cm)
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Subjective Questions
1 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Single Correct
23 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Objective
42 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
A wooden plank of mass 20kg is resting on a smooth horizontal floor. A man of mass 60kg starts moving from one end of the plank to the other end. The length of the plank is 10m. Find the displacement of the plank over the floor when the man reaches the other end of the plank.

View SolutionA balloon is moving upwards with velocity 10m/s. It releases a stone which comes down to the ground in 11s. The height of the balloon from the ground at the moment when the stone was dropped is (g=10m/s2)
View SolutionA boy throws a ball with a velocity of 15 m/s at an angle of 15° with the horizontal. The distance at which the ball strikes the ground is
View SolutionTwo men to masses 80kg and 60kg are standing on a wood plank of mass 100kg, that has been placed over a smooth surface. If both the men start moving towards each other with speeds 1m/s and 2m/s respectively then find the velocity of the plank by which it starts moving.
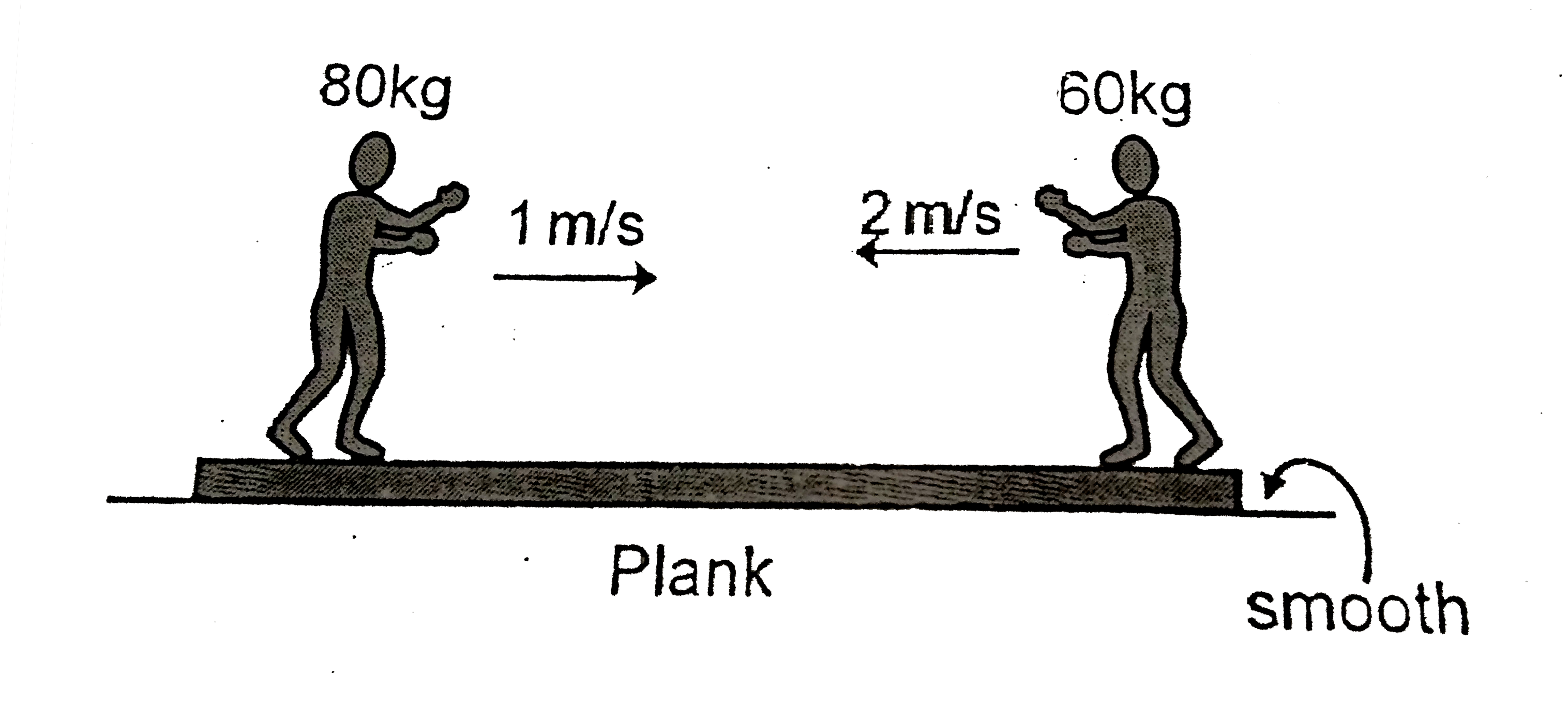
View SolutionA boy throws a stone with a speed of V0=10 m/sec at an angle of θ0=30∘ to the horizontal Find the position of the stone wrt the point of projection just after a time t = 1/2 sec.
View SolutionA block A of mass 2 kg rests on a horizontal surface. Another block B of mass 1 kg moving at a speed of m/s when at a distance of 16 cm from A. collides elastically with A. The coefficeint of friction between the horizontal surface and earth of the blocks is 0.2. Then (g=10m/s2)
View SolutionA block of mass m slides over a smooth wedge of mass M which is placed over a rough horizontal surface . The centre of mass of the system will move towards left

Here μ = coefficient of friction between the wedge and the ground .
View SolutionA particle of mass 1kg has been thrown with initial speed 20 ms making an angle 60° with the horizontal ground. the angular momentum of the particle about point of projection when the projectile is at highest point is (g=10m/s^2)
View SolutionA skater of mass m standing on ice throws a stone of mass M with a velocity of v in a horizontal direction. The distance over which the skater will move back (the coefficient of friction between the skater and the ice is μ)
View SolutionA boy of mass 25 kg stands on a board of mass 10 kg which in turn is kept on a frictionless horizontal ice surface. The boy makes a jump with a velocity component 5m/s in a horizontal direction with respect to the ice. With what velocity does the board recoil? With what rate are the boy and the board seperate from each other?
View Solution
