A boy stands at 39.2 m from a building and throws a ball which just passes through a window 19.6 m above the ground. Calculate the velocity of projection of the ball.
To solve the problem step by step, we will use the concepts of projectile motion.
Step 1: Identify the given data
- Distance from the building (horizontal distance, R) = 39.2 m
- Height of the window (maximum height, H) = 19.6 m
- Acceleration due to gravity (g) = 9.8 m/s²
Step 2: Use the formula for maximum height
The formula for the maximum height H reached by a projectile is given by:
H=u2sin2θ2g
Where:
- u = initial velocity of projection
- θ = angle of projection
Step 3: Use the formula for range
The formula for the range R of a projectile is given by:
R=u2sin2θg
Step 4: Relate the two equations
From the two equations, we can express H and R in terms of u and θ:
1. From the maximum height equation:
H=u2sin2θ2g(1)
2. From the range equation:
R=u2sin2θg(2)
Step 5: Substitute R in terms of H
From equation (1), we can express u2sin2θ:
u2sin2θ=2gH
From equation (2), we can express u2sin2θ:
u2sin2θ=gR
Since sin2θ=2sinθcosθ, we can rewrite equation (2) as:
u2⋅2sinθcosθ=gR
Step 6: Divide the two equations
Now, we can divide the two equations:
u2sin2θu2⋅2sinθcosθ=2gHgR
This simplifies to:
sinθ2cosθ=HR
Substituting the values of H and R:
sinθ2cosθ=19.639.2
This simplifies to:
sinθ2cosθ=12
Thus, we find:
tanθ=1
This implies:
θ=45∘
Step 7: Substitute θ back to find u
Now substituting θ=45∘ back into equation (1):
H=u2sin245∘2g
Since sin45∘=1√2:
19.6=u2(1√2)22⋅9.8
This simplifies to:
19.6=u2⋅1219.6
Multiplying both sides by 2⋅19.6:
u2=4⋅19.6
Calculating u:
u=√78.4≈8.85 m/s
Final Answer
The velocity of projection of the ball is approximately 8.85m/s.
- Distance from the building (horizontal distance, R) = 39.2 m
- Height of the window (maximum height, H) = 19.6 m
- Acceleration due to gravity (g) = 9.8 m/s²
The formula for the maximum height H reached by a projectile is given by:
H=u2sin2θ2g
Where:
- u = initial velocity of projection
- θ = angle of projection
The formula for the range R of a projectile is given by:
R=u2sin2θg
From the two equations, we can express H and R in terms of u and θ:
1. From the maximum height equation:
H=u2sin2θ2g(1)
2. From the range equation:
R=u2sin2θg(2)
From equation (1), we can express u2sin2θ:
u2sin2θ=2gH
From equation (2), we can express u2sin2θ:
u2sin2θ=gR
Since sin2θ=2sinθcosθ, we can rewrite equation (2) as:
u2⋅2sinθcosθ=gR
Now, we can divide the two equations:
u2sin2θu2⋅2sinθcosθ=2gHgR
This simplifies to:
sinθ2cosθ=HR
Substituting the values of H and R:
sinθ2cosθ=19.639.2
This simplifies to:
sinθ2cosθ=12
Thus, we find:
tanθ=1
This implies:
θ=45∘
Now substituting θ=45∘ back into equation (1):
H=u2sin245∘2g
Since sin45∘=1√2:
19.6=u2(1√2)22⋅9.8
This simplifies to:
19.6=u2⋅1219.6
Multiplying both sides by 2⋅19.6:
u2=4⋅19.6
Calculating u:
u=√78.4≈8.85 m/s
The velocity of projection of the ball is approximately 8.85m/s.
Topper's Solved these Questions
- BOOK - SL ARORACHAPTER - Motion in a PlaneEXERCISE - Excercise397videos
Motion in a Plane
- BOOK - SL ARORACHAPTER - Motion in a PlaneEXERCISE - Excercise397videos
Motion in a Plane
- BOOK - SL ARORACHAPTER - MECHANICSEXERCISE - Exercise341videos
MECHANICS
- BOOK - SL ARORACHAPTER - MOTION IN ONE DIMENSIONEXERCISE - problems for self practice66videos
MOTION IN ONE DIMENSION
Similar Questions
A body stans at 78.4m from a building and throws a ball which just enters a window 39.2m above the ground. Calculate the velocity of projection of the ball. Fig. 2 (d) . 22.
 . View Solution
. View SolutionA boy stands 19.6 m away from a 9.8m high cliff. If the throws a ball towards the cliff such that it just passes above from it , find the velocity of projection of the ball.
View Solution
Knowledge Check
- Question 1 - Select One
From the top of a building 80mhigh, a ball is thrown horizontally which hits the ground at a distance.The line joining the top of the building to the point where it hits the ground makes an angle of 45∘ with the ground. Initial velocity of projection of the ball is (g=10m/s2)
A10m/sB15m/sC20m/sD30m/s - Question 2 - Select One
A ball is thrown vertically upwards from the ground and a student gazing out of the window sees it moving upward past him at 10ms−1. The window is at 15 m above the ground level. The velocity of ball 3 s after it was projected from the ground is [Take g=10ms−2]
A10m/s, upB20m/s, upC20ms−1,downD10ms−1, down - Question 3 - Select One
Two rings are suspended from the points A and B on the ceiling of a room with the help of strings of length 1.2 m each as shown. The points A and B are separated from each other by a distance AB = 1.2 m. A boy standing on the floor throws a small ball so that it passes through the two rings whose diameter is slightly greater than the ball. At the moment when the boy throws the ball, his hand is at a height of 1.0 m above the floor. A stop watch which is switched on at the moment of throwing the ball reads 0.2 s when the ball passes through the first ring and 0.6 s when it passes through the second ring.
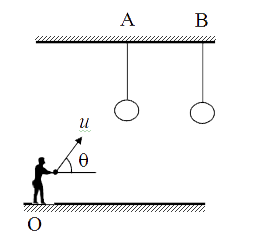
The projection speed of the ball is:A3 m/sB4 m/sC5 m/sD2.5 m/s
A cricketer can throw a ball to a maximum horizontal distance of 100 m. How high above the ground can the cricketer throw the same ball ?
View SolutionA circus artist maintains four balls in motion making each in turn to rise to a height of 5 m from hishand. Calculate the velocity with which he projects the balls. Where will the other three balls be at the instant when the fourth one is just leaving his hand ? Take g=10m/s2
View SolutionTwo tall buildings are 40m apart A ball thrown horizontally from a window 145m above the ground in one building is to enter a window 22.5m above the ground in the other building. The speed of the ball should be
View SolutionTwo tall buildings are 40m apart. A ball thrown horizontally from a window 145m above the ground in one building is to enter a window 22.5m above the ground in the other building.The speed of the ball should be (A) 6m/s (B) 8m/s (C) 10m/s (D) 12m/s
View SolutionTwo rings are suspended from the points A and B on the ceiling of a room with the help of strings of length 1.2 m each as shown. The points A and B are separated from each other by a distance AB = 1.2 m. A boy standing on the floor throws a small ball so that it passes through the two rings whose diameter is slightly greater than the ball. At the moment when the boy throws the ball, his hand is at a height of 1.0 m above the floor. A stop watch which is switched on at the moment of throwing the ball reads 0.2 s when the ball passes through the first ring and 0.6 s when it passes through the second ring.
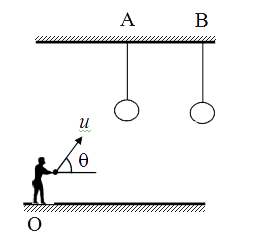
The angle of projection of the ball is:View Solution

