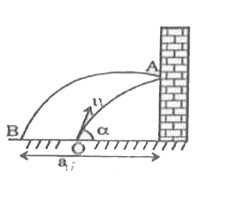
A boy throws a ball with initial speed $\sqrt{a g}$ at an angle $θ$ to the horizontal. It strikes a smooth vertical wall and returns to his hand. Show that if the boy is standing at a distance 'a' from the wall, the coefficient of restitution between the ball and the wall equals $\frac{1}{(4 sin 2 θ - 1)}$ . Also show that $θ$ cannot be less than $15^{\circ}$ .

Text Solution

Verified by Experts

The correct Answer is:NA

Updated on:21/07/2023

A ball is projected at $t = 0$ with velocity $v_{0}$ at angle $θ$ with horizontal. It strikes a smooth wall at a distance from it and then falls at a distance d from the wall. Coefficient of restitution is 'e' then :
ABall will return to ground at $t = \frac{2 v_{0} sin θ}{g}$
B $d = e (R - L) (where R is \frac{v_{0} sin 2 θ}{g})$
Cmaximum height during motion $= \frac{v_{0}^{2} {sin}^{2} θ}{2 g}$
Dit will return to ground at $t < \frac{2 v_{0} sin θ}{g}$
A girl throws a ball with an initial velocity v at an angle $45^{\circ}$ . The ball strikes a smooth vertical wall at a horizontal distance d from the girl and after rebound returns to her hands. What is the coefficient of restitution between wall and ball ? $(v^{2} > d g)$
A $\frac{v^{2} - g d}{g d}$
B $\frac{g d}{v^{2} - g d}$
C $\frac{g d}{v^{2}}$
D $\frac{v^{2}}{g d}$