A bullet fired into a fixed target loses half of its velocity in penetrating 15 cm. How much further it will penetrate before coming to rest?
5 cm
15 cm
7.5 cm
10 cm
The correct Answer is:A
To solve the problem step by step, we will use the equations of motion to find how much further the bullet penetrates before coming to rest.
Step 1: Understand the given data
- The bullet loses half of its velocity when it penetrates 15 cm.
- Let the initial velocity of the bullet be u.
- After penetrating 15 cm, the final velocity v becomes u2.
Step 2: Use the third equation of motion
We will use the third equation of motion:
v2=u2+2as
where:
- v=u2
- u=u
- s=15cm
- a is the acceleration (deceleration in this case).
Substituting the values into the equation:
(u2)2=u2+2a(15)
This simplifies to:
u24=u2+30a
Step 3: Rearranging the equation
Rearranging the equation gives:
u24−u2=30a
−3u24=30a
Thus, we can solve for a:
a=−3u2120=−u240
Step 4: Find the further penetration distance
Now, we need to find how much further the bullet will penetrate before coming to rest. The final velocity v=0 and the initial velocity for this part of the motion is u2.
Using the same equation of motion:
v2=u2+2as
Substituting the known values:
0=(u2)2+2(−u240)s0
This simplifies to:
0=u24−u220s0
Step 5: Solve for s0
Rearranging gives:
u220s0=u24
Dividing both sides by u2 (assuming u≠0):
s020=14
Thus:
s0=20×14=5cm
Conclusion
The bullet will penetrate a further distance of 5 cm before coming to rest.
---
- The bullet loses half of its velocity when it penetrates 15 cm.
- Let the initial velocity of the bullet be u.
- After penetrating 15 cm, the final velocity v becomes u2.
We will use the third equation of motion:
v2=u2+2as
where:
- v=u2
- u=u
- s=15cm
- a is the acceleration (deceleration in this case).
(u2)2=u2+2a(15)
This simplifies to:
u24=u2+30a
Rearranging the equation gives:
u24−u2=30a
−3u24=30a
Thus, we can solve for a:
a=−3u2120=−u240
Now, we need to find how much further the bullet will penetrate before coming to rest. The final velocity v=0 and the initial velocity for this part of the motion is u2.
v2=u2+2as
Substituting the known values:
0=(u2)2+2(−u240)s0
This simplifies to:
0=u24−u220s0
Rearranging gives:
u220s0=u24
Dividing both sides by u2 (assuming u≠0):
s020=14
Thus:
s0=20×14=5cm
The bullet will penetrate a further distance of 5 cm before coming to rest.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - PRACTICE EXERCISE
58 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - problems
47 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - EXERCISE -I
58 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III
49 Videos
Similar Questions
A bullet fired into a fixed target loses half of its velocity after penetrating 3 cm . How much further it will penetrate before coming to rest assuming that it faces constant resistance to motion?
View SolutionA body loses half of its velocity on penetrating 6 cm in wooden block. How much will it penetrate more before coming to rest ?
View Solution
Knowledge Check
A bullet fired into a wooden block loses half of its velocity after penetrating 40 cm. It comes to rest after penetrating a further distance of
A22/3 cmB40/3 cmC20/3 cmD22/5 cm
If a body looses half of its velocity on penetrating 3 cm in a wooden block, then how much will it penetrate more before coming to rest?
View SolutionIf a body looses half of its velocity on penetrating 3 cm in a wooden block, then how much will it penetrate more before coming to rest?
View SolutionThe speed of a train is reduced from 60 km/h, to 15 km/h, while it travels a distance of 450 m. If the retardation is uniform, find how much further it will travel before coming to rest ?
View SolutionWhen a celling fan is switched off, its angular velocity falls to half while it makes 36 rotations. How many more rotations will it make before coming to rest ?
View SolutionWhen a celling fan is switched off, its angular velocity falls to half while it makes 36 rotations. How many more rotations will it make before coming to rest ?
View SolutionA bullet of mass 5 g travels with a speed of 500 ms−1 .if it penetrates a fixed target which offers a constant resistive force of 1000 N to the motion of the bullet ,find ,(a) the intial Kinetic energy of the bullet penetrated before coming to rest,and (c)the speed with which the bullet emerges out of the target if target is of thickness 0.5 m.
View SolutionA frequently used device to measure the speed of bullets is the ballistic pendulum. It comprises of a heavy block of wood of mass M suspended by two long chords. A bullet of mass m is fired into the block horizontally. The block, with the bullet embedded in it, swings upwards. The centre of mass of the combination rises through a vertical distance h before coming to rest momentarily. In a particular experiment, a bullet of mass 40 gm is fired into a wooden block of mass 10 kg. The block is observed to rise by a height of 20.0 cm.
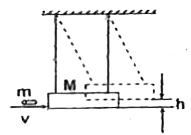
If the bullet penetrates the block to a depth of 3.0 cm, the approximate average force of resistance by the block of wood is
View Solution
