A bullet is fired on a fixed target. It penetrates inside the target through distance d=3.75cm and then stops. mass of the bullet is m=1kg and of the target is M=4kg. Now an identical bullet moving with the same velocity is fired on the identical target which is placed at rest on a frictionless horizontal surface. Then find the distance (in cm) to which the bullet will penetrate inside the target?
The correct Answer is:3
To solve the problem step by step, we will analyze the two scenarios given: the bullet penetrating a fixed target and the bullet penetrating a target that is free to move.
Step 1: Understand the first scenario
In the first case, a bullet of mass m=1kg is fired at a fixed target of mass M=4kg and penetrates a distance d=3.75cm. The work done by the bullet on the target is equal to the change in kinetic energy of the bullet.
Equation:
W=−F⋅d=−12mu2
Where F is the resistive force exerted by the target on the bullet.
Step 2: Set up the equation for the first case
From the work-energy principle, we can write:
−F⋅d=−12mu2
This simplifies to:
F⋅d=12mu2(1)
Step 3: Understand the second scenario
In the second case, an identical bullet is fired at an identical target, but this time the target is free to move on a frictionless surface. When the bullet strikes the target, both the bullet and the target will move together after the collision.
Step 4: Use conservation of momentum
Using the conservation of momentum, we have:
mu=(M+m)V
Where V is the final velocity of both the bullet and the target after the collision. Rearranging gives:
V=muM+m(2)
Step 5: Calculate the kinetic energy after the collision
The kinetic energy after the collision can be expressed as:
KE=12(M+m)V2
Substituting V from equation (2):
KE=12(M+m)(muM+m)2
This simplifies to:
KE=12m2u2M+m(3)
Step 6: Set up the work-energy equation for the second case
The work done on the target in the second case can also be expressed as:
−F⋅d′=KE
Where d′ is the distance penetrated in the second case. Thus:
F⋅d′=12m2u2M+m(4)
Step 7: Relate equations (1) and (4)
From equations (1) and (4), we can set up the ratio:
F⋅dF⋅d′=12mu212m2u2M+m
This simplifies to:
dd′=M+mm
Step 8: Solve for d′
Rearranging gives:
d′=d⋅mM+m
Substituting d=3.75cm, m=1kg, and M=4kg:
d′=3.75⋅14+1=3.75⋅15=0.75cm
Final Answer
The distance to which the bullet will penetrate inside the target is d′=0.75cm.
---
In the first case, a bullet of mass m=1kg is fired at a fixed target of mass M=4kg and penetrates a distance d=3.75cm. The work done by the bullet on the target is equal to the change in kinetic energy of the bullet.
W=−F⋅d=−12mu2
Where F is the resistive force exerted by the target on the bullet.
From the work-energy principle, we can write:
−F⋅d=−12mu2
This simplifies to:
F⋅d=12mu2(1)
In the second case, an identical bullet is fired at an identical target, but this time the target is free to move on a frictionless surface. When the bullet strikes the target, both the bullet and the target will move together after the collision.
Using the conservation of momentum, we have:
mu=(M+m)V
Where V is the final velocity of both the bullet and the target after the collision. Rearranging gives:
V=muM+m(2)
The kinetic energy after the collision can be expressed as:
KE=12(M+m)V2
Substituting V from equation (2):
KE=12(M+m)(muM+m)2
This simplifies to:
KE=12m2u2M+m(3)
The work done on the target in the second case can also be expressed as:
−F⋅d′=KE
Where d′ is the distance penetrated in the second case. Thus:
F⋅d′=12m2u2M+m(4)
From equations (1) and (4), we can set up the ratio:
F⋅dF⋅d′=12mu212m2u2M+m
This simplifies to:
dd′=M+mm
Rearranging gives:
d′=d⋅mM+m
Substituting d=3.75cm, m=1kg, and M=4kg:
d′=3.75⋅14+1=3.75⋅15=0.75cm
The distance to which the bullet will penetrate inside the target is d′=0.75cm.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - SCQ_TYPE
12 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Linked Comprehension
105 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A bullet is fired on a fixed target. It penetrates inside the target through distance d = 4 cm and then stops, mass of bullet is m = 1kg and of target is M = 4kg . Now identical bullet moving with same velocity is fired on identical which is placed at rest on frictionless horizontal surface. The distance ( in mm ) to which the bullet will penetrate inside the target is 4K ( mm). Find K .
View SolutionA bullet moving with a velocity of 30√2ms−1 is fired into a fixed target. It penetrated into the target to the extent of s metres. If the same bullet is fired into a target of thickness s2 metres and of the same material with the same velocity, then the bullet comes out of the target with velocity
View SolutionA bulley with muzzle velocity 100ms−1 is to be shot at a target 30m away in the same horizontal line. How high above the target must the rifle be aimed so that the bullet will hit the target ?
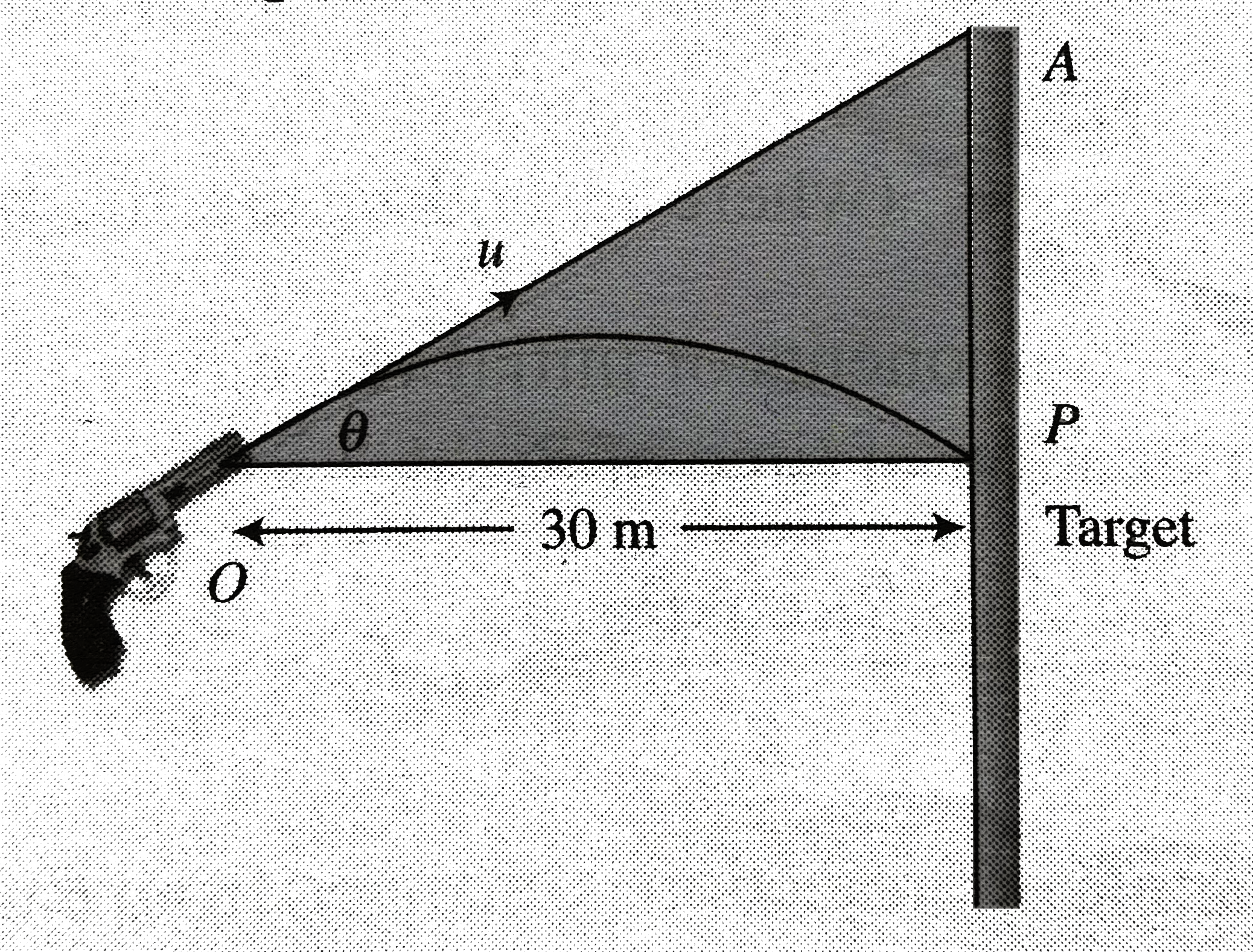 .
.
View SolutionA loaded spring gun of mass M fires a bullet of mass m with a velocity v at an angle of elevation θ. The gun is initially at rest on a horizontal smooth surface. After firing, the centre of mass of the gun and bullet system
View SolutionA loaded spring gun of mass M fires a bullet of mass m with a velocity v at an angle of elevation θ. The gun is initially at rest on a horizontal smooth surface. After firing, the centre of mass of the gun and bullet system
View SolutionA large number of bullets are fired in all directions with the same speed v. Find the maximum area on the ground on which these bullets will spread.
View SolutionA bullet of mass m and velocity v is fired into a large block of mass M. The final velocity of the system is
View SolutionA bullet initially moving with a velocity 20 m s−1 strikes a target and comes to rest after penetrating a distance 10 cm in the target. Calculate the retardation caused by the target.
View SolutionA bullet fired into a fixed target loses half of its velocity in penetrating 15 cm. How much further it will penetrate before coming to rest?
View SolutionTwo bullets are fired simultaneously, horizontally and with different speeds from the same place. Which bullet will hit the ground first?
View Solution
