Figure shows position and velocities of two particles moving under mutual gravitational attraction in space at time t=0. The position of centre of mass after one second is
'*'m. Fill '*'.

The correct Answer is:8
As →Fext=0,→acm=0
→Vcm=2×8ˆi−3×2ˆi2+3=2ˆi
xcm=2×3+3×82+3=6m
As →Vcm is constant
Therefore CM will move 2m in 1s.
∴6+2=8m
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - SCQ_TYPE12videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Linked Comprehension105videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
Knowledge Check
- Question 1 - Select One
Two particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of each particle is
A12R√(1Gm)B√(Gm2R)C12√(GmR)D√(4GmR)
Figure shows the position of a particle moving on the X-axis as a function of time.
 View Solution
View SolutionAt t=0, the positions and velocities of two particles are as shown in the figure. They are kept on a smooth surface and being mutually attracted by gravitational force. Find the position of centre of mass at t=2s.
 .View Solution
.View SolutionAt t=0, the positions and velocities of two particles are as shown in the figure. They are kept on a smooth surface and being mutually attracted by gravitational force. Find the position of centre of mass at t=2s.
 .View Solution
.View SolutionFigure shows the position-time graph of a particle moving on the X--axis. Which of these option correctly describes the particle 's motion?
 View Solution
View SolutionFigure shows the velocity time graph of a particle moving along straight line (v is m/s and t is in second). It average velocity in 20 seconds will be:
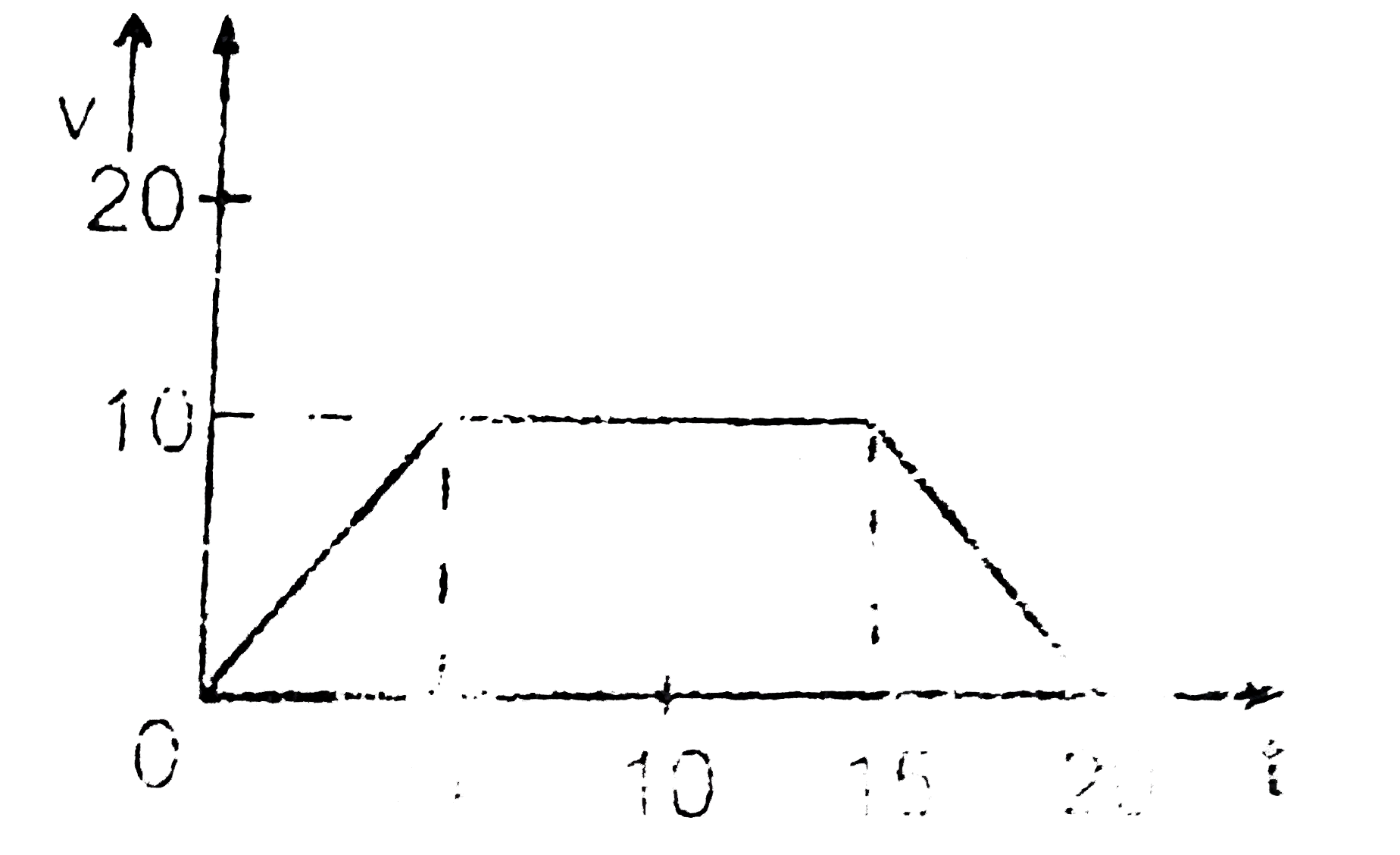 .View Solution
.View SolutionFind the velocity of a particle moving on a line at t = 3 seconds , if its position s is in m when
s = log t andView SolutionTwo particles of equal mass go round a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View Solution