A bullet of mass 0.01kg and travelling at a speed of 500ms−1 strikes a block of mass 2kg which is suspended by a string of length 5m. The centre of gravity of the block is found to raise a vertical distance of 0.2m. What is the speed of the bullet after it emerges from the block?
15ms−1
20ms−1
100ms−1
50ms−1
The correct Answer is:C
To solve the problem, we will use the principles of conservation of momentum and conservation of energy.
Step 1: Understand the problem
We have a bullet of mass m1=0.01kg traveling at a speed u1=500m/s that strikes a block of mass m2=2kg. The block is suspended and rises to a height h=0.2m after the collision. We need to find the speed of the bullet after it emerges from the block, denoted as v1.
Step 2: Apply conservation of momentum
Before the collision, the total momentum is given by:
pinitial=m1u1+m2⋅0=0.01⋅500+0=5kg m/s
After the collision, let v1 be the speed of the bullet and v2 be the speed of the block. The total momentum after the collision is:
pfinal=m1v1+m2v2
Setting the initial momentum equal to the final momentum, we have:
5=0.01v1+2v2(1)
Step 3: Apply conservation of energy
The kinetic energy before the collision is:
KEinitial=12m1u21=12⋅0.01⋅(500)2=1250J
After the collision, the kinetic energy of the bullet and block plus the potential energy gained by the block is:
KEfinal=12m1v21+12m2v22+mgh
where h=0.2m and g=10m/s2. The potential energy gained by the block is:
PE=m2gh=2⋅10⋅0.2=4J
Setting the initial kinetic energy equal to the final kinetic energy plus potential energy, we have:
1250=12⋅0.01v21+12⋅2v22+4(2)
Step 4: Solve the equations
From equation (1):
2v2=5−0.01v1⟹v2=5−0.01v12
Substituting v2 into equation (2):
1250=12⋅0.01v21+12⋅2(5−0.01v12)2+4
Simplifying:
1250−4=0.012v21+12⋅2⋅(5−0.01v1)24
1246=0.005v21+(5−0.01v1)24
Expanding the square:
1246=0.005v21+25−0.1v1+0.0001v214
Multiplying through by 4 to eliminate the fraction:
4984=0.02v21+25−0.1v1
Rearranging gives:
0.02v21+0.1v1−4960=0
This is a quadratic equation in v1.
Step 5: Solve the quadratic equation
Using the quadratic formula v1=−b±√b2−4ac2a:
Here, a=0.02, b=0.1, and c=−4960.
Calculating the discriminant:
D=b2−4ac=(0.1)2−4⋅0.02⋅(−4960)=0.01+396.8=396.81
Calculating v1:
v1=−0.1±√396.812⋅0.02
Calculating √396.81≈19.93:
v1=−0.1±19.930.04
Taking the positive root:
v1=19.830.04≈495.75m/s
Step 6: Find v2
Using v2 from equation (1):
v2=5−0.01⋅495.752≈1.21m/s
Final Result
The speed of the bullet after it emerges from the block is approximately 495.75m/s.
We have a bullet of mass m1=0.01kg traveling at a speed u1=500m/s that strikes a block of mass m2=2kg. The block is suspended and rises to a height h=0.2m after the collision. We need to find the speed of the bullet after it emerges from the block, denoted as v1.
Before the collision, the total momentum is given by:
pinitial=m1u1+m2⋅0=0.01⋅500+0=5kg m/s
After the collision, let v1 be the speed of the bullet and v2 be the speed of the block. The total momentum after the collision is:
pfinal=m1v1+m2v2
Setting the initial momentum equal to the final momentum, we have:
5=0.01v1+2v2(1)
The kinetic energy before the collision is:
KEinitial=12m1u21=12⋅0.01⋅(500)2=1250J
After the collision, the kinetic energy of the bullet and block plus the potential energy gained by the block is:
KEfinal=12m1v21+12m2v22+mgh
where h=0.2m and g=10m/s2. The potential energy gained by the block is:
PE=m2gh=2⋅10⋅0.2=4J
Setting the initial kinetic energy equal to the final kinetic energy plus potential energy, we have:
1250=12⋅0.01v21+12⋅2v22+4(2)
From equation (1):
2v2=5−0.01v1⟹v2=5−0.01v12
Substituting v2 into equation (2):
1250=12⋅0.01v21+12⋅2(5−0.01v12)2+4
Simplifying:
1250−4=0.012v21+12⋅2⋅(5−0.01v1)24
1246=0.005v21+(5−0.01v1)24
Expanding the square:
1246=0.005v21+25−0.1v1+0.0001v214
Multiplying through by 4 to eliminate the fraction:
4984=0.02v21+25−0.1v1
Rearranging gives:
0.02v21+0.1v1−4960=0
This is a quadratic equation in v1.
Using the quadratic formula v1=−b±√b2−4ac2a:
Here, a=0.02, b=0.1, and c=−4960.
Calculating the discriminant:
D=b2−4ac=(0.1)2−4⋅0.02⋅(−4960)=0.01+396.8=396.81
Calculating v1:
v1=−0.1±√396.812⋅0.02
Calculating √396.81≈19.93:
v1=−0.1±19.930.04
Taking the positive root:
v1=19.830.04≈495.75m/s
Using v2 from equation (1):
v2=5−0.01⋅495.752≈1.21m/s
The speed of the bullet after it emerges from the block is approximately 495.75m/s.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct25videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning2videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective23videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
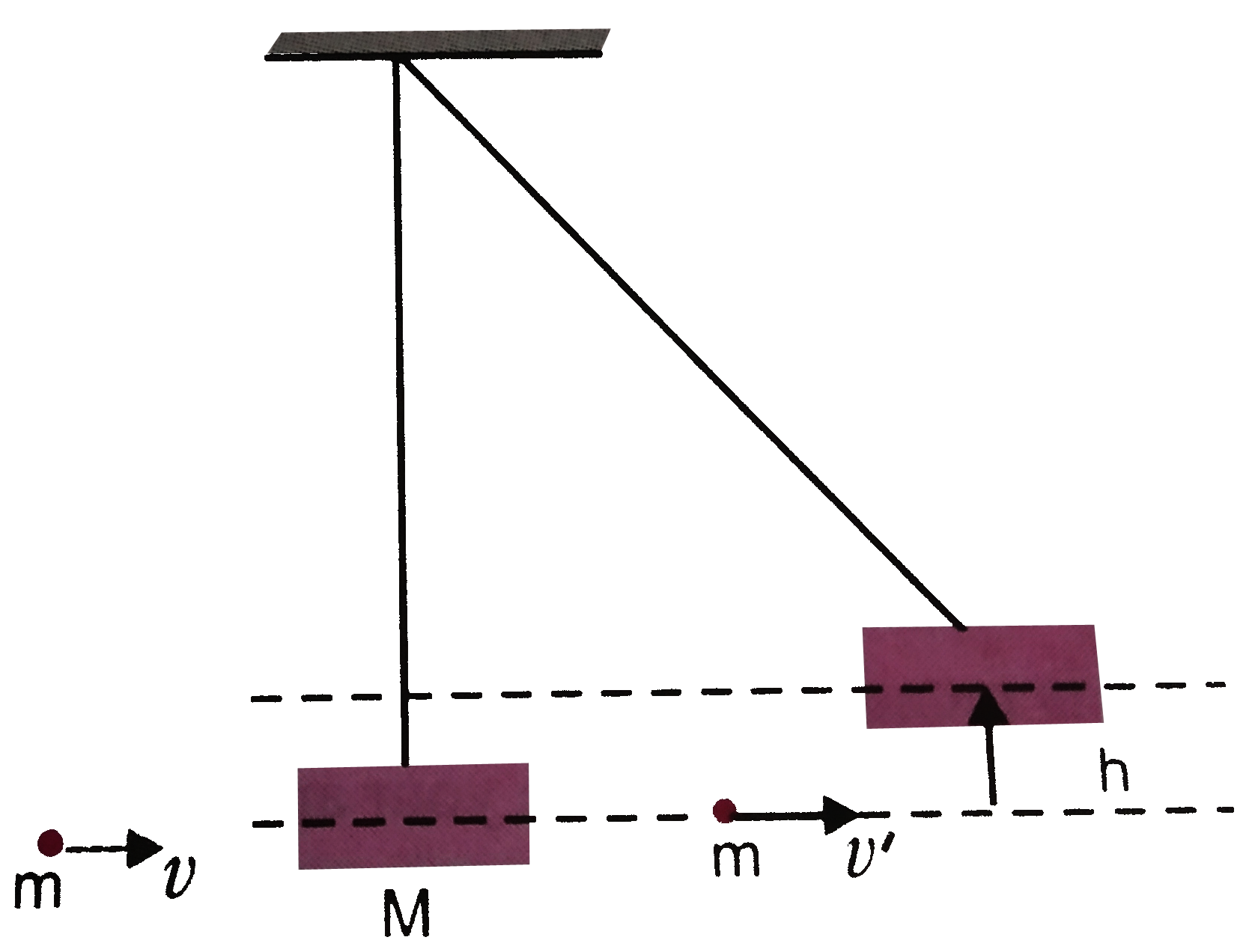
A bullet of mass 0.01 kg and travelling at a speed of 500 m/s strikes a block of mass 2 kg which is suspended by a string of length 5m. The center of gravity of the block is found to rise a vertical distance of 0.1m, figure. What is the speed of the bullet after it emerges from the block ? (g=9.8m/s2).
 View Solution
View SolutionA bullet of mass 10g moving horizontally with a velocity of 400ms−1 strickes a wooden block of mass 2kg which is suspended by a light inextensible string of length 5m. As a result, the center ofgravity of the block is found to rise a vertical distance of 10cm . The speed of the bullet after it emerges out hirizontally from the block will be
View SolutionA bullet of mass 10g moving horizontally with a velocity of 400ms−1 strickes a wooden block of mass 2kg which is suspended by a light inextensible string of length 5m. As a result, the center ofgravity of the block is found to rise a vertical distance of 10cm . The speed of the bullet after it emerges out hirizontally from the block will be
View SolutionA bullet of mass 20 g moving horizontally at a speed of 300 m/s is fired into a wooden block of mass 500 g suspended by a long string. The bullet crosses the block and emerges on the other side. If the centre of mass of the block rises through a height of 20.0 cm, find the speed of the bullet as it emerges from the block.
View SolutionA bullet of mass 0.005 kg moving with a speed of 200 ms−1 enters a heavy wooden block and is stopped after a distance of 50 cm. What is the average force exerted by the block on the bullet?
View SolutionA bullet of mass 0.04 kg moving with a speed of 600 m/s penetrates a heavy wooden block. It stops after a penetration of 500 cm. The resistive force exerted by the block on the bullet is
View SolutionA bullet of mass 0.1 kg is fired with a speed of 100 m/sec , the mass of gun is 50 kg . The velocity of recoil is
View SolutionA bullet of mass 0.1 kg is fired with a speed of 100 m/sec , the mass of gun is 50 kg . The velocity of recoil is
View SolutionA bullet of mass 0.04 kg moving with a speed of 90ms−1 enters a heavy wooden block and is stooped after a distance of 60 cm . What is the average resistive force exerted by the block on the bullet ?
View SolutionA block of mass 1kg moving with a speed of 4ms−1, collides with another block of mass 2kg which is at rest. The lighter block comes to rest after collision. The loss in KE of the system is
View Solution

