A bullet of mass 10g moving horizontally with a velocity of 400ms−1 strickes a wooden block of mass 2kg which is suspended by a light inextensible string of length 5m. As a result, the center ofgravity of the block is found to rise a vertical distance of 10cm . The speed of the bullet after it emerges out hirizontally from the block will be
100 ms−1
80 ms−1
120 ms−1
160 ms−1
The correct Answer is:C
To solve the problem step by step, we will use the principles of conservation of momentum and conservation of energy.
Step 1: Understanding the Problem
We have a bullet of mass m=10g=0.01kg moving with a velocity u=400m/s that strikes a wooden block of mass M=2kg. After the collision, the center of gravity of the block rises by h=10cm=0.1m.
Step 2: Apply Conservation of Energy
The initial kinetic energy of the bullet is converted into potential energy of the block and the kinetic energy of the bullet after it exits the block.
The potential energy gained by the block when it rises to height h is given by:
PE=Mgh
Substituting the values:
PE=2kg×10m/s2×0.1m=2kg×10×0.1=2J
Step 3: Write the Energy Conservation Equation
The initial kinetic energy of the bullet is:
KEinitial=12mu2=12×0.01kg×(400m/s)2
Calculating this:
KEinitial=12×0.01×160000=800J
The final kinetic energy of the bullet after passing through the block is:
KEfinal=12mv21
where v1 is the speed of the bullet after it exits the block.
Step 4: Set Up the Energy Conservation Equation
According to the conservation of energy:
KEinitial=PE+KEfinal
Substituting the known values:
800J=2J+12×0.01kg×v21
This simplifies to:
800−2=12×0.01×v21
798=12×0.01×v21
Step 5: Solve for v1
Multiply both sides by 2:
1596=0.01×v21
Dividing by 0.01:
v21=159600
Taking the square root:
v1=√159600≈399.5m/s
Step 6: Apply Conservation of Momentum
Now, we can use conservation of momentum to find the final speed of the bullet after it exits the block. The initial momentum is:
Pinitial=mu=0.01×400=4kg m/s
The final momentum is:
Pfinal=mv1+Mv2
where v2 is the velocity of the block after the collision.
Using the height gained, we can find v2 using energy conservation:
12Mv22=Mgh
Substituting:
12×2v22=2×10×0.1
v22=2×2=4⟹v2=2m/s
Step 7: Substitute into Momentum Equation
Now substituting back into the momentum equation:
4=0.01v1+2
Solving for v1:
4−2=0.01v1
2=0.01v1⟹v1=20.01=200m/s
Conclusion
The speed of the bullet after it emerges horizontally from the block is approximately 200m/s.
We have a bullet of mass m=10g=0.01kg moving with a velocity u=400m/s that strikes a wooden block of mass M=2kg. After the collision, the center of gravity of the block rises by h=10cm=0.1m.
The initial kinetic energy of the bullet is converted into potential energy of the block and the kinetic energy of the bullet after it exits the block.
PE=Mgh
Substituting the values:
PE=2kg×10m/s2×0.1m=2kg×10×0.1=2J
The initial kinetic energy of the bullet is:
KEinitial=12mu2=12×0.01kg×(400m/s)2
Calculating this:
KEinitial=12×0.01×160000=800J
KEfinal=12mv21
where v1 is the speed of the bullet after it exits the block.
According to the conservation of energy:
KEinitial=PE+KEfinal
Substituting the known values:
800J=2J+12×0.01kg×v21
This simplifies to:
800−2=12×0.01×v21
798=12×0.01×v21
Multiply both sides by 2:
1596=0.01×v21
Dividing by 0.01:
v21=159600
Taking the square root:
v1=√159600≈399.5m/s
Now, we can use conservation of momentum to find the final speed of the bullet after it exits the block. The initial momentum is:
Pinitial=mu=0.01×400=4kg m/s
The final momentum is:
Pfinal=mv1+Mv2
where v2 is the velocity of the block after the collision.
12Mv22=Mgh
Substituting:
12×2v22=2×10×0.1
v22=2×2=4⟹v2=2m/s
Now substituting back into the momentum equation:
4=0.01v1+2
Solving for v1:
4−2=0.01v1
2=0.01v1⟹v1=20.01=200m/s
The speed of the bullet after it emerges horizontally from the block is approximately 200m/s.
Similar Questions
A bullet of mass 0.01kg and travelling at a speed of 500ms−1 strikes a block of mass 2kg which is suspended by a string of length 5m. The centre of gravity of the block is found to raise a vertical distance of 0.2m. What is the speed of the bullet after it emerges from the block?
View SolutionA bullet of mass 0.01 kg and travelling at a speed of 500 m/s strikes a block of mass 2 kg which is suspended by a string of length 5m. The center of gravity of the block is found to rise a vertical distance of 0.1m, figure. What is the speed of the bullet after it emerges from the block ? (g=9.8m/s2).
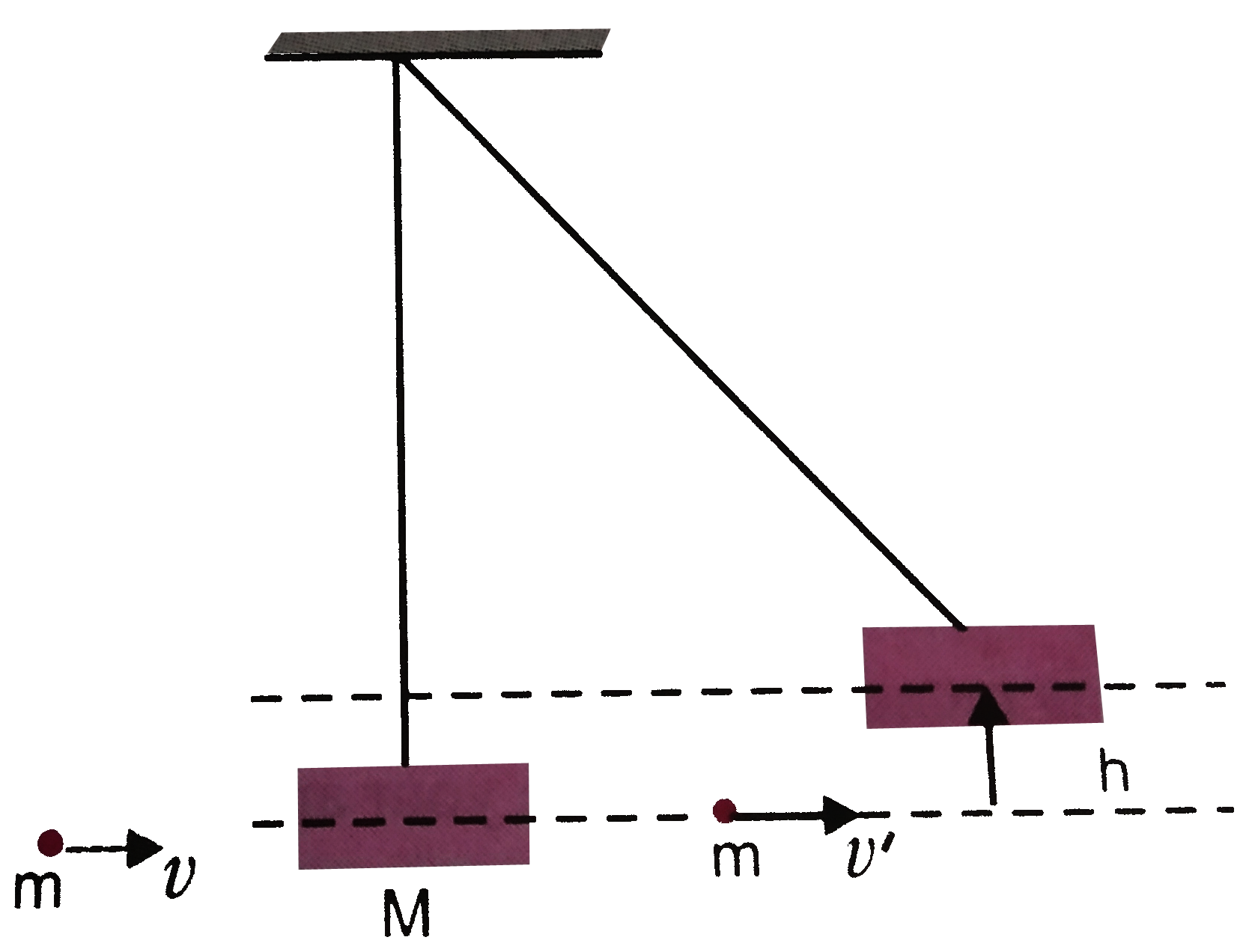
View SolutionA bullet of mass 20 g moving horizontally at a speed of 300 m/s is fired into a wooden block of mass 500 g suspended by a long string. The bullet crosses the block and emerges on the other side. If the centre of mass of the block rises through a height of 20.0 cm, find the speed of the bullet as it emerges from the block.
View Solution
A block of mass m is suspended from one end of a light spring as shown. The origin O is considered at distance equal to natural length of the spring from the ceiling and vertical downwards direction as positive y-axis. When the system is in equilibrium a bullet of mass m3 moving in vertical up wards direction with velocity v0 strikes the block and embeds into it. As a result, the block (with bullet embedded into it) moves up and start oscillating. Based on the given information, answer the following question:
Q. The time taken by the block bullet system to move from y=mgk (initial equilibrium position) to y=0 (natural length of spring) is (A represents the amplitude of motion)
View SolutionA bullet of mass 20 g travelling horizontally at 100ms−1 gets embedded at the centre of a block of wood of mass 1kg, suspended by a light vertical string of 1m in length. Calculate the maximum inclination of the string to the vertical.
View SolutionA bullet of mass 50 g moving with an initial velocity 100m s−1 strikes a wooden block and comes to rest after penetrating a distance 2 cm in it. Calculate : Final momentum of the bullet
View SolutionA bullet of mass 50 g moving with an initial velocity 100m s−1 strikes a wooden block and comes to rest after penetrating a distance 2 cm in it. Calculate : Initial momentum of the bullet
View SolutionA bullet of mass 10 g moving with a velocity 300ms−1 strikes a wooden block and comes out from ot her side with a velocity of 200ms−1. Find the work done by t he resistive force on the bullet.
View SolutionA bullet of mass 10 g moving with a velocity 300ms−1 strikes a wooden block and comes out from ot her side with a velocity of 200ms−1. Find the work done by t he resistive force on the bullet.
View SolutionA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is

View Solution
