A bullet of mass strikes an obstacle and moves at to its original direction. If its speed also changes from to . Find the magnitude of impulse acting on the bullet.
The correct Answer is:A, B, C
To find the magnitude of the impulse acting on the bullet, we will follow these steps:
Step 1: Identify the given data
- Mass of the bullet, m=10−3kg
- Initial speed, v1=20m/s
- Final speed, v2=10m/s
- Angle of deflection, θ=60∘
Step 2: Calculate the initial momentum
The initial momentum of the bullet can be calculated as:
p1=m⋅v1=10−3kg⋅20m/s=2×10−2kg m/s
Step 3: Resolve the final velocity into components
The final velocity v2 can be resolved into two components:
1. Along the original direction (x-direction):
v2x=v2⋅cos(60∘)=10⋅12=5m/s
2. Perpendicular to the original direction (y-direction):
v2y=v2⋅sin(60∘)=10⋅√32=5√3m/s
Step 4: Calculate the final momentum components
1. Final momentum in the x-direction:
p2x=m⋅v2x=10−3⋅5=5×10−3kg m/s
2. Final momentum in the y-direction:
p2y=m⋅v2y=10−3⋅5√3=5√3×10−3kg m/s
Step 5: Calculate the change in momentum
1. Change in momentum in the x-direction:
Δpx=p2x−p1=5×10−3−2×10−2=−1.5×10−2kg m/s
2. Change in momentum in the y-direction:
Δpy=p2y−0=5√3×10−3kg m/s
Step 6: Calculate the impulse components
1. Impulse in the x-direction:
Jx=Δpx=−1.5×10−2N s
2. Impulse in the y-direction:
Jy=Δpy=5√3×10−3N s
Step 7: Calculate the magnitude of the net impulse
The magnitude of the net impulse can be calculated using the Pythagorean theorem:
J=√J2x+J2y
Substituting the values:
J=√(−1.5×10−2)2+(5√3×10−3)2
Calculating:
J=√(2.25×10−4)+(75×10−6)=√(2.25×10−4)+(7.5×10−5)=√3×10−4=√3×10−2N s
Final Answer
The magnitude of the impulse acting on the bullet is:
J=√3×10−2N s
- Mass of the bullet, m=10−3kg
- Initial speed, v1=20m/s
- Final speed, v2=10m/s
- Angle of deflection, θ=60∘
The initial momentum of the bullet can be calculated as:
p1=m⋅v1=10−3kg⋅20m/s=2×10−2kg m/s
The final velocity v2 can be resolved into two components:
1. Along the original direction (x-direction):
v2x=v2⋅cos(60∘)=10⋅12=5m/s
2. Perpendicular to the original direction (y-direction):
v2y=v2⋅sin(60∘)=10⋅√32=5√3m/s
1. Final momentum in the x-direction:
p2x=m⋅v2x=10−3⋅5=5×10−3kg m/s
2. Final momentum in the y-direction:
p2y=m⋅v2y=10−3⋅5√3=5√3×10−3kg m/s
1. Change in momentum in the x-direction:
Δpx=p2x−p1=5×10−3−2×10−2=−1.5×10−2kg m/s
2. Change in momentum in the y-direction:
Δpy=p2y−0=5√3×10−3kg m/s
1. Impulse in the x-direction:
Jx=Δpx=−1.5×10−2N s
2. Impulse in the y-direction:
Jy=Δpy=5√3×10−3N s
The magnitude of the net impulse can be calculated using the Pythagorean theorem:
J=√J2x+J2y
Substituting the values:
J=√(−1.5×10−2)2+(5√3×10−3)2
Calculating:
J=√(2.25×10−4)+(75×10−6)=√(2.25×10−4)+(7.5×10−5)=√3×10−4=√3×10−2N s
The magnitude of the impulse acting on the bullet is:
J=√3×10−2N s
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Type 1
1 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Solved Examples
13 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
A bullet of mass m strikes an obstruction and deviates off at 60° to its original direction. If its speed is also changed from u to v, find the magnitude of the impulse acting on the bullet.
View SolutionA cricket ball of mass 160g is moving horizontally directly towards a batsman. Its speed just before it hits the bat is 30m/s. It leaves the bat at 40m/s at 90∘ to its original direction. Find the magnitude of the impulse (in N−s) imparted to the ball.
View Solution
Knowledge Check
A ball of mass m travelling horiozntally with velocity v strikes a massive vertical wall and rebounds back along its original direction with no change in speed. What is the magnitude of the impulse delivered by the wall to the ball?
A0B12mvCmvD2mvA constant force acting on a body of mass of 5 kg change its speed from 5ms−1to10ms−1 in 10 s without changing the direction of motion. The force acting on the body is
A1.5NB2NC2.5ND5N
Certain force acting on a 20 kg mass changes its velocity from 5m/s→2m/s. calculate the work done by the force.
View SolutionA ball of mass 1kg strikes a heavy plarform elastically, moving upwards with a velocity of 5m/s . The speed of the ball just before the collision is 10m/s downwards. Then the impulse imparted by the platform on the ball is

View SolutionA particle is projected at an angle 60∘ with horizontal with a speed v=20m/s. Taking g=10m/s2. Find the time after which the speed of the particle remains half of its initial speed.
View SolutionA bullte of mass 10gm in moving with speed 400m/s. Find its kinetic energy in calories?
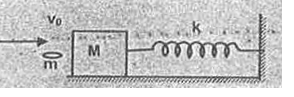
View SolutionA bullet of mass m strikes a block of mass M connected to a light spring of stiffness k, with a speed v0 and gets into it. Find the loss of K.E. of the bullet.
View SolutionA bullet of mass 10g travelling horizontally with a velocity of 150ms−1 strikes a stationary wooden block and come to rest in 0.03s. Calculate the distance of penetration of the bullet into the block. Also, Calculate the magnitude of the force exerted by the wooden block on the bullet,
View Solution
