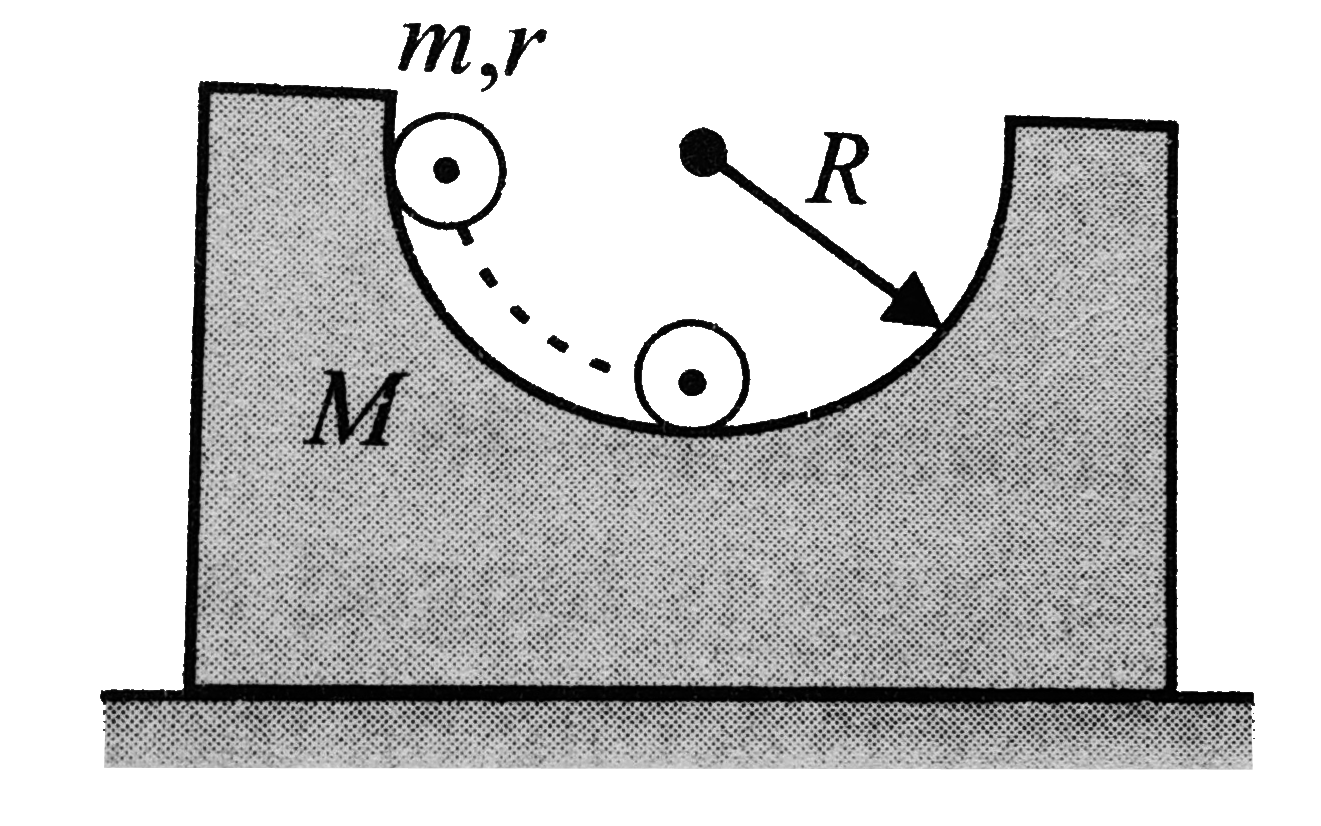
A small cube of mass m slides down a circular path of radius R cut into a large block of mass M, as shown in figure. M rests on a table, and both blocks move without friction. The blocks are initially at rest, and m starts from the top of the path. Find the horizontal distance from the bottom of block where cube hits the cable

The correct Answer is:B

mv1=Mv2 …(i)
mgR=12mv21+12Mv22 …(ii)
t=√2(R/2)g=√Rg …(iii)
The desired distance is
S=(v1+v2)t …(iv)
Solving Eqs. (i) and (ii) of v1 and v2 and substituting in Eq. (iv), we get
S=R√2M+mM
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Comprehension Based Questions3videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions15videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery19videos
CIRCULAR MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
A block of mass 3 kg slides down an inclined plane of length 6 m and height 4 m. if the force of friction on the block is a constant 16 N as it slides from rest at the top of the incline, what is its speed at the bottom?
A2m/sB3m/sC4m/sD5m/s
A uniform solid cylinder of mass 2kg and radius 0.2m is released from rest at the top of a semicircular track of radius 0.7m cut in a block of mass M=3kg as shown in Fig. The block is resting on a smooth horizontal surface and the cylinder rolls down without slipping. Based on the above information, answer the following questions:

The distance moved by the block when the cylinder reaches the bottom of the track isView SolutionA small block of mass m slides along a smooth frictional track as shown in the figure. If it starts from rest at P, what is the resultant force acting on it at Q?
 View Solution
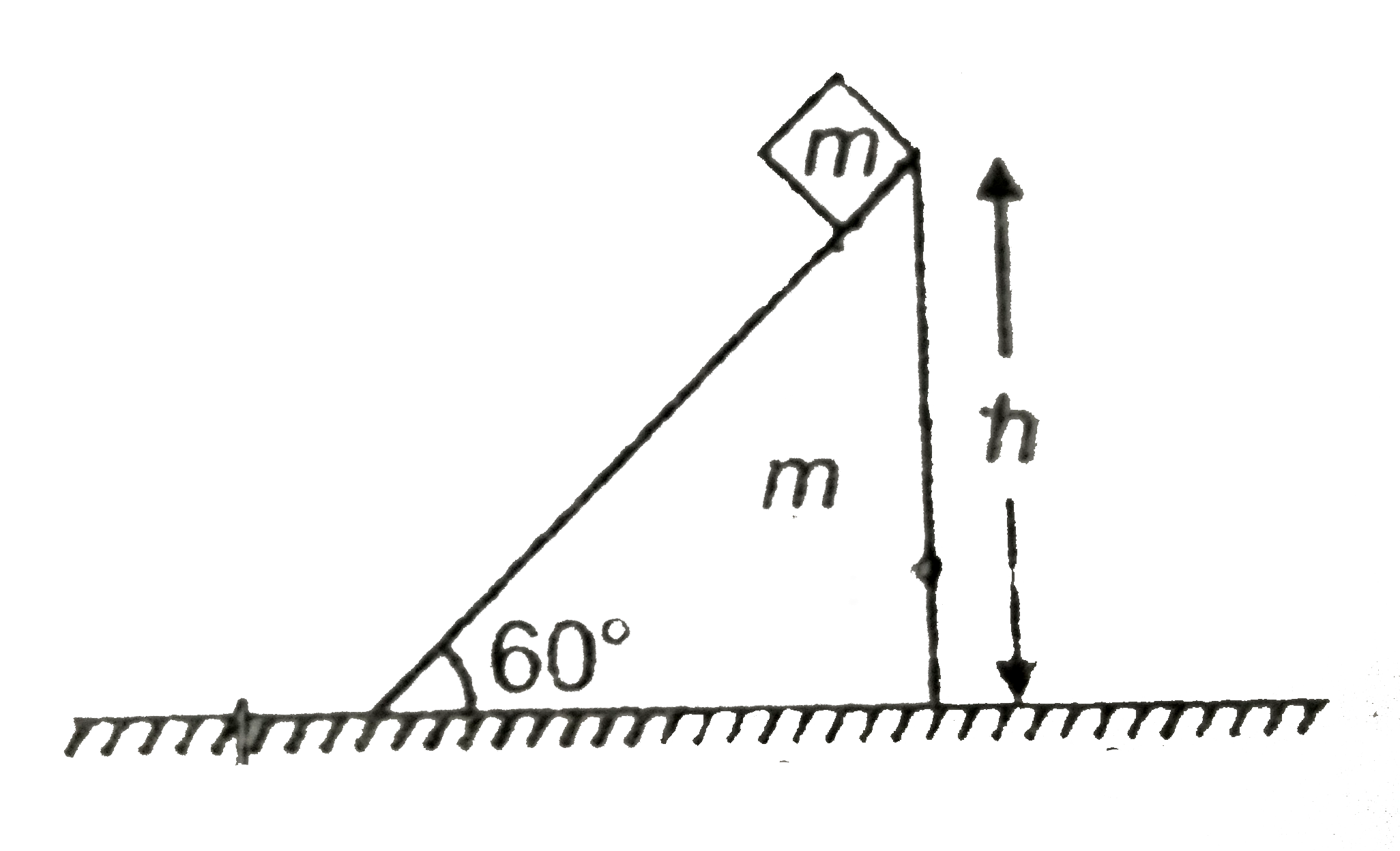
View SolutionThe block of mass m is at rest. Find the tension in the string A .
 View Solution
View SolutionA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure Choose the wrong option.
 View Solution
View SolutionA uniform solid cylinder of mass 2kg and radius 0.2m is released from rest at the top of a semicircular track of radius 0.7m cut in a block of mass M=3kg as shown in Fig. The block is resting on a smooth horizontal surface and the cylinder rolls down without slipping. Based on the above information, answer the following questions:
The speed of the point of contact of the cylinder with the block w.r.t. ground, when the cylinder reaches the bottom of the track isView SolutionA block of mass m is released from a wedge of mass m as shown in figure . Find the time taken by the block to reach the end of the wedge.
 View Solution
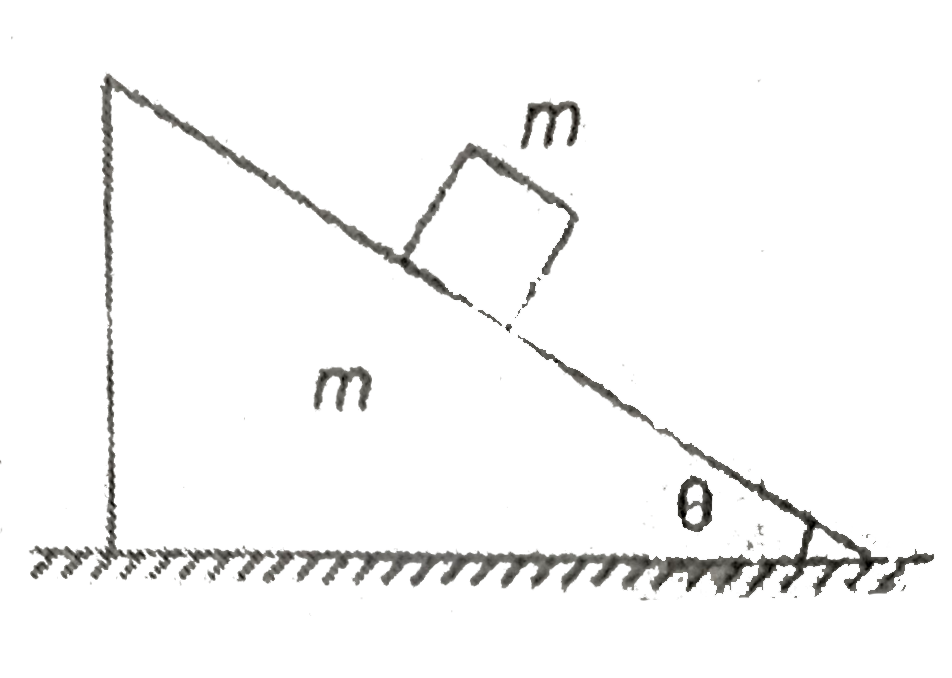
View SolutionA block of mass m slides down on inclined wedge of same mass m as shown in figure . Friction is absent everywhere . Acceleration of centre of mass of the block and wedge is
 View Solution
View Solution


