A small block of mass m is placed on top of a smooth hemisphere also of mass m which is placed on a smooth horizontal surface. If the block begins to slide down due to a negligible small impulse, show that it will loose contact with the hemisphere when the radial line through vertical makes an angle θ given by the equaition cos3θ−6cosθ+4=0.

Let vr be the relative velocity of block as it leaves contact with the sphere (N=0) and v the horizontal velocity of sphere at this instant.

Applying conservation of linear momentum in horizontal direction, we get
mv=m(vrcosθ−v)
or 2v=vrcosθ ...(i)
Conservation of mechanincal energy gives,
mgr(1−cosθ)=12mv2+12m(v2r+v2−2vvrcosθ)
or gr(1−cosθ)=v2+v2r2−vvrcosθ ...(ii)
Equation of laws of motion gives,
mgcosθ=mv2rr or gr=v2rcosθ ...(iii)
Solving Eqs. (i), (ii) and (ii), we get
cos3θ−6cosθ+4=0
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Comprehension Based Questions
3 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
A small block of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. If h be the height of wedge and θ is the inclination, then the distance moved by the wedge as the block reaches the foot of the wedge is
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of mass m slides over a smooth wedge of mass M which is placed over a rough horizontal surface . The centre of mass of the system will move towards left

Here μ = coefficient of friction between the wedge and the ground .
View SolutionA small body of mass 'm' is placed at the top of a smooth sphere of radius 'R' placed on a horizontal surface as shown, Now the sphere is given a constant horizontal acceleration a0=g. The velocity of the body relative to the sphere at the moment when it loses contact with the sphere is

View SolutionA force P acts on a smooth block of mass m placed on a horizontal floor at an angle θ with with horizontal on the block

View SolutionA block B of mass 0.6kg slides down the smooth face PR of a wedge A of mass 1.7kg which can move freely on a smooth horizontal surface.
The inclination of the face PR to the horizontal is 45∘ . Then :

View SolutionA small block of mass m is released from rest from point A inside a smooth hemispher bowl of radius R, which is fixed on ground such that OA is horizontal. The ratio (x) of magnitude of centripetal force and normal reaction on the block at any point B varies with θ as :
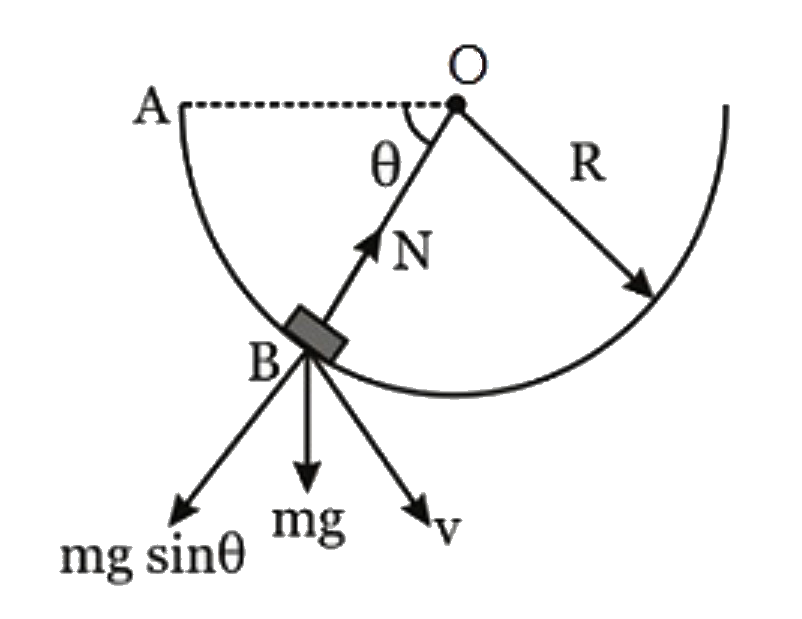
View SolutionA small block of mass m is released from rest from point A inside a smooth hemisphere bowl of radius R, which is fixed on group such that OA is horizontal. The ratio (x) of magnitude of centripetal force and normal reaction on the block at any point B varies with θ as :

View SolutionA small block of mass m has speed√gR2 at the top most point of a fixed hemisphere of radius R as shown in figure. The angle θ, when block loses the contact with the hemisphere is
_PHY_E05_149_Q01.png)
View Solution
