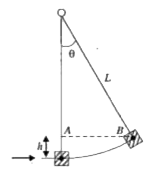
A bullet of mass m moving with horizontal velocity v strikes a stationary block of mass M suspended by a string of length L. Then bullet gets embedded in the block. What is the maximum angle made by the string after impact?
Let the block and the bullet rise to a height h from Fig.
cosθ=OAOB=L−hL
L−h=Lcosθ
h=L(1−costhea) ……….(i)
Applying the law of conservation of linear momentum,
mv=(m+M)V
Where V is the velocity of the block bullet system
V=mvm+M ...........(ii)
Applying the law of conservation of energy 12(m+M)V2=(M+m)gh
Substituting the value of V from equation (ii) and h from equation (i),
12m2v2(m+M)2=gL(1−cosθ)
cosθ=1−m2v22(m+M)2gL
θ=cos−1[1−m2v22(m+M)2gL]
Topper's Solved these Questions
- BOOK - ICSECHAPTER - DYNAMICSEXERCISE - ADDITIONAL SOLVED PROBLEMS138videos
DYNAMICS
- BOOK - ICSECHAPTER - DYNAMICSEXERCISE - CONCEPTUAL SHORT ANSWER QUESTIONS WITH ANSWERS20videos
DYNAMICS
- BOOK - ICSECHAPTER - DIMENSIONSEXERCISE - SELECTED PROBLEMS (FROM CONVERSIONS OF ONE SYSTEMS OF UNITS INTO ANOTHER)9videos
DIMENSIONS
- BOOK - ICSECHAPTER - FRICTIONEXERCISE - Selected problems30videos
FRICTION
Similar Questions
A bullet of mass m moving with a horizontal velocity u strikes a stationary wooden block of mass M suspended by a string of length L = 50 cm. The bullet emerges out of the block with speed u4. If M = 6 m, minimum value of u so that the block can complete the vertical circle (take, g = 10 ms−2)
View SolutionA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A bullet of mass m moving with a horizontal velocity u strikes a stationary wooden block of mass M suspended by a string of length L = 50 cm. The bullet emerges out of the block with speed u4. If M = 6 m, minimum value of u so that the block can complete the vertical circle (take, g = 10 ms−2)
A10 ms−1B20 ms−1C30 ms−1D40 ms−1 - Question 2 - Select One
A bullet of mass m moving with a speed v strikes a wooden block of mass M & gets embedded into the block. The final speed is
A√MM+nVB√mM+nVCmM+nVDV2 - Question 3 - Select One
A bullet of mass 20g moving horizontally strikes a block of mass 480g suspended by a string of length 2m. If the collision is completely inelastic , the minimum velocity of bullet , so that the combined mass complete vertical circle should be
A100m/sB150m/sC200m/sD250m/s
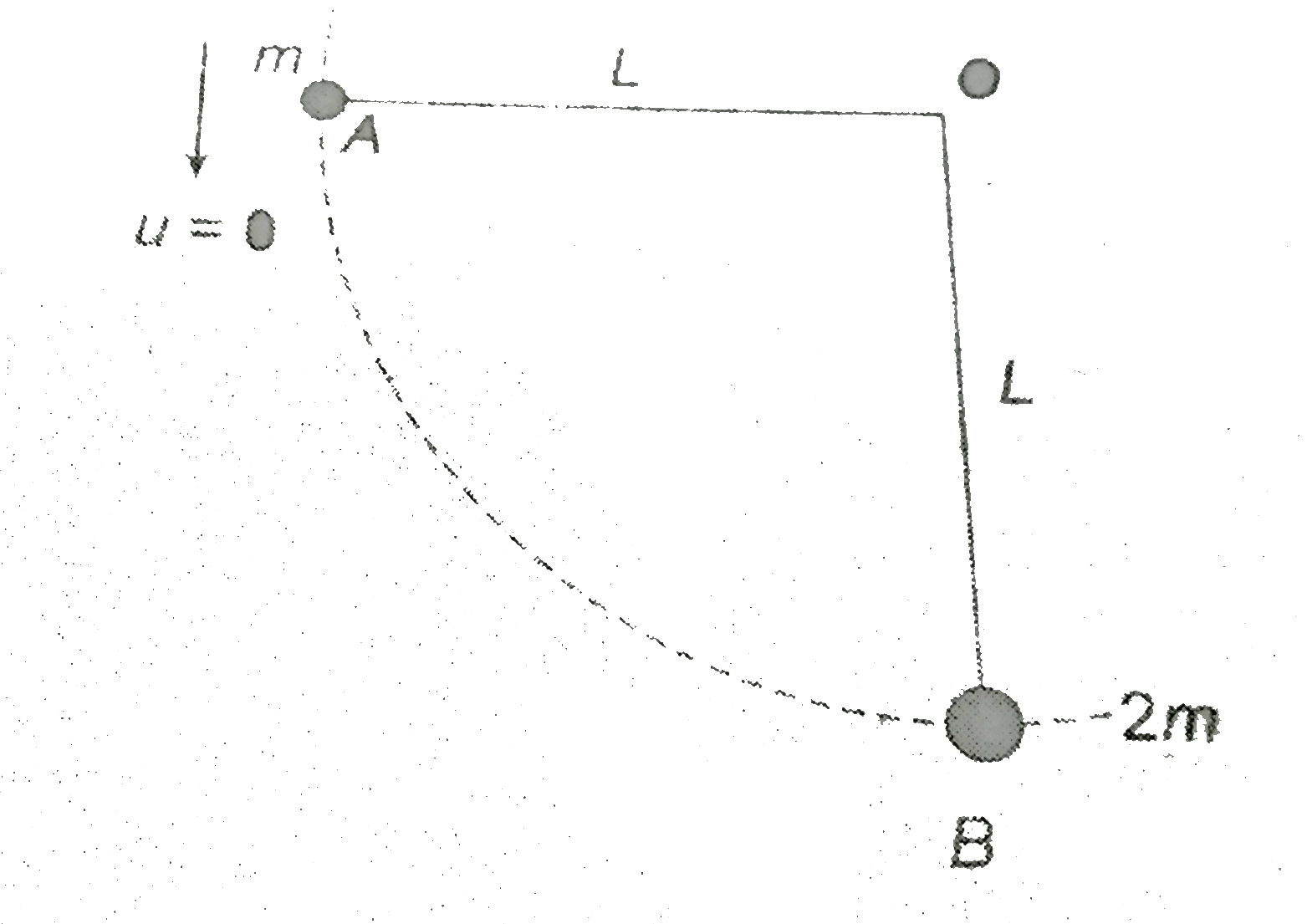
A ball A of mass m attached to a string of length L is released when the string is horizontal. It strikes another ball B of mass 2m suspended to another string of length L at rest as shown. Find the maximum angle made by the string if the collision is completely inelastic.
 View Solution
View SolutionA bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is
 View Solution
View SolutionA bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionA bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View Solution
