Question

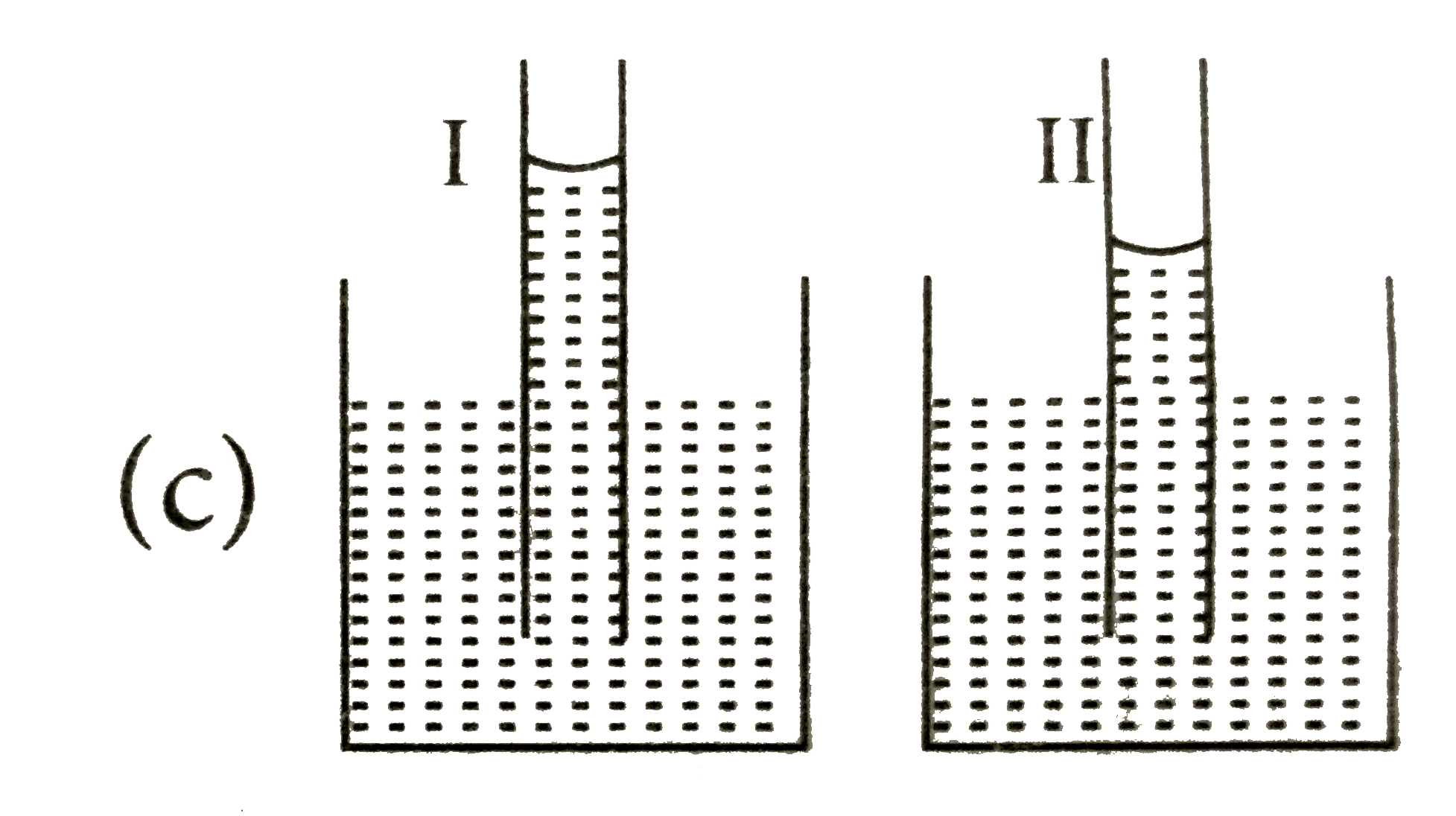
A capillary tube (A) is dipped in water. Another identical tube (B) is dipped in a soap-water solution. Which of the following shows the relative nature of the liquid columns in the two tubes?

Options

A.
B.
C.
D.

Answer

C

Explanation

To solve the problem of comparing the liquid columns in two identical capillary tubes, one dipped in water and the other in a soap-water solution, we can follow these steps:

Step 1: Understand Capillary Action
Capillary action occurs due to the interplay of cohesive and adhesive forces in a liquid. When a liquid is in contact with a solid surface (like the walls of a capillary tube), the adhesive forces between the liquid and the solid can cause the liquid to rise in the tube.

Step 2: Identify the Liquids
- Tube A: Dipped in water.
- Tube B: Dipped in a soap-water solution.

Step 3: Analyze Surface Tension
Surface tension plays a crucial role in capillary action. Water has a relatively high surface tension, while soap-water solutions have a lower surface tension due to the presence of surfactants.

Step 4: Apply the Capillary Rise Formula
The height of the liquid column (h) in a capillary tube can be described by the formula:
\( h = \frac{2T \cos \theta}{R \rho g} \)
Where:
- \( T \) = surface tension of the liquid
- \( \theta \) = contact angle
- \( R \) = radius of the tube
- \( \rho \) = density of the liquid
- \( g \) = acceleration due to gravity

Step 5: Compare the Two Tubes
- For Tube A (water): Water has a higher surface tension, leading to a certain height of rise.
- For Tube B (soap-water solution): The surface tension is lower, which means the height of the liquid column will be less compared to that in tube A.

Step 6: Conclusion
Since the surface tension of the soap-water solution is lower than that of water, the liquid column in Tube A (water) will rise higher than in Tube B (soap-water solution). Therefore, the relative heights of the liquid columns will show that Tube A has a higher liquid column than Tube B.

Final Answer
The correct option is that the liquid column in Tube A (water) will be higher than the liquid column in Tube B (soap-water solution).

---