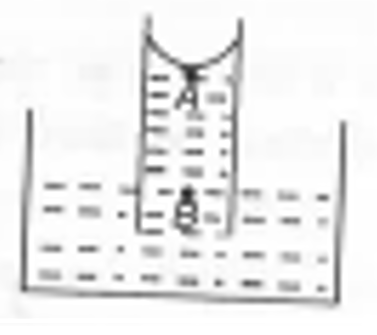
A capillary tube is dipped in a liquid. Let pressure at point $A, B$ and $C$ be $p_{A} p_{B}$ and $p_{C}$ respectively, then

1) p A = p B = p C
2)p A = p B < p C
3)p A = p C < p B
4)p A = p C > p B

$p_{A} = p_{B} = p_{C}$

$p_{A} = p_{B} < p_{C}$

$p_{A} = P_{C} < p_{B}$

$p_{A} = p_{C} > p_{B}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$p_{A} = p_{C} = p_{0} and p_{B} = p_{0} - \frac{2 T}{R}$

Class 11 PHYSICS MECHANICAL PROPERTIES OF FLUIDS

Topper's Solved these Questions

FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - B) Medical entrance special format question
19 Videos
FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Match the columns
6 Videos
FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.4
10 Videos
EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos

Knowledge Check

An experiment yields 3 mutually exclusive and exclusive events A, B and C . If P(A) = 2P(B) = 3 P( C ) , then P(A) is equal to
A $\frac{1}{11}$
B $\frac{2}{11}$
C $\frac{3}{11}$
D $\frac{6}{11}$

In a triangle $A B C$ , let P and Q be points on AB and AC respectively such that $P Q ∣ ∣ B C$ . Prove that the median $A D$ bisects $P Q$ .
View Solution
Triangle ABC has right angle at B and contains a point P for which $P A = 10, P B = 6$ and $∠ A P B = ∠ B P C = ∠ C P A,$ then $(\frac{P C}{11})$ is
View Solution
In $A B C$ , $P$ and $Q$ are points on sides $A B$ and $A C$ respectively such that $P Q ∣ ∣ B C$ . If $A P = 3 c m$ , $P B = 5 c m$ and $A C = 8 c m$ , find $A Q$ .
View Solution
In a right triangle $A B C$ right-angled at $B,$ if $P a n d Q$ are points on the sides $A B a n d A C$ respectively, then (a) $A Q^{2} + C P^{2} = 2 (A C^{2} + P Q^{2})$ (b) $2 (A Q^{2} + C P^{2}) = A C^{2} + P Q^{2}$ (c) $A Q^{2} + C P^{2} = A C^{2} + P Q^{2}$ (d) $A Q + C P = \frac{1}{2} (A C + P Q) .$
View Solution
$P$ and $Q$ are points on the sides $C A$ and $C B$ respectively of $A B C$ , right-angled at $C$ . Prove that $A Q^{2} + B P^{2} = A B^{2} + P Q^{2}$ .
View Solution
If $a, b, a n d c$ are in A.P. $p, q, a n d r$ are in H.P., and $a p, b q, a n d c r$ are in G.P., then $\frac{p}{r} + \frac{r}{p}$ is equal to a/c+c/a
View Solution
The plots of $\frac{1}{X_{A}} v s . \frac{1}{Y_{A}}$ (where $X_{A}$ and $Y_{A}$ are the mole fraction of liquid $A$ in liquid and vapour phase respectively) is linear with slope and intercept respectively are given as:
(a) $\frac{P_{A}^{\circ}}{P_{B}^{\circ}}, \frac{P_{B}^{\circ} - P_{A}^{\circ}}{P_{B}^{\circ}}$
(b) $\frac{P_{B}^{\circ}}{P_{A}^{\circ}}, \frac{P_{A}^{\circ} - P_{B}^{\circ}}{P_{A}^{\circ}}$
(c) $\frac{P_{B}^{\circ}}{P_{A}^{\circ}}, \frac{P_{B}^{\circ}}{P_{B}^{\circ} - P_{A}^{\circ}}$
(d) $P_{A}^{\circ} - P_{B}^{\circ}, \frac{P_{A}^{\circ}}{P_{B}^{\circ}}$
View Solution

DC PANDEY ENGLISH-FLUID MECHANICS-Taking it together

A sphere of solid material of specific gravity 8 has a concentric sphe...
05:16
A cubical block of side 10 cm floats at the interface of an oil and wa...
02:53
A liquid stands at the plane level in the U-tube when at rest. If area...
03:03
A capillary tube is dipped in a liquid. Let pressure at point A,B and ...
02:18
The volume of an air bubble becomes three times as it rises from the b...
02:14
Water falls from a tap with A(0)=4 m^(2), A=1 m^(2) and h=2 m, then ve...
04:59
A ball of relative density 0.8 falls into water from a height of 2 m. ...
06:38
A pump is designed as a horizontal cylinder with a piston of area A an...
06:21
If cross- sectional area of limb I is A(1) and that of limb II is A(2)...
03:12
Two capillaries of same length and radii in the ratio 1:2 are connecte...
03:12
A thread is tied slightly loose to a wire frame as in figure and the f...
01:29
A tank filled with water has two taps to exhaust and pour. A hollow sp...
03:16
A container is partially filled with a liquid of density rho2 A capill...
02:34
A ball of mass 1 kg falls from a height of 5m above the free surface o...
06:59
Under isothermal condition two soap bubbles of radii r(1) and r(2) coa...
04:20
A bent tube is lowered into a water stream as shown in figure. The vel...
04:39
A soild ball of density half that of water falls freely under gravity ...
03:38
A large tank is filled with water (density = 10^(3) kg//m^(3)). A smal...
04:30
A wooden plank of length 1m and unform cross-section is hinged at one ...
07:26
Air is blown through a pipe AB at a rate of 15 litres per minute. The ...
05:22

Home
Ask Doubt
Profile

A capillary tube is dipped in a liquid. Let pressure at point A,B and C be pApB and pC respectively, then 1) p A = p B = p C 2)p A = p B < p C 3)p A = p C < p B 4)p A = p C > p B

The correct Answer is:D

pA=pC=p0 andpB=p0−2TR

Topper's Solved these Questions

Similar Questions

Knowledge Check

An experiment yields 3 mutually exclusive and exclusive events A, B and C . If P(A) = 2P(B) = 3 P( C ) , then P(A) is equal to

DC PANDEY ENGLISH-FLUID MECHANICS-Taking it together

A capillary tube is dipped in a liquid. Let pressure at point $A, B$ and $C$ be $p_{A} p_{B}$ and $p_{C}$ respectively, then

1) p A = p B = p C
2)p A = p B < p C
3)p A = p C < p B
4)p A = p C > p B

$p_{A} = p_{C} = p_{0} and p_{B} = p_{0} - \frac{2 T}{R}$