A car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β and ultimately comes to rest.If the total time-lapse is t, what is the total distance described and maximum velocity reached ?
The correct Answer is:12αβt2α+β,αβtα+β
To solve the problem, we will break it down into steps to find the total distance traveled by the car and the maximum velocity reached.
Step 1: Define Variables
Let:
- α = acceleration of the car
- β = deceleration of the car
- t = total time of travel
- t1 = time of acceleration
- t2 = time of deceleration
- vmax = maximum velocity reached
Step 2: Relate Time of Acceleration and Deceleration
Since the car accelerates for time t1 and decelerates for time t2, we have:
t1+t2=t
Step 3: Find Maximum Velocity
During acceleration, the maximum velocity vmax can be expressed as:
vmax=αt1
During deceleration, the relationship between initial velocity, final velocity, and time can be used:
0=vmax−βt2⟹vmax=βt2
Equating the two expressions for vmax:
αt1=βt2
From this, we can express t2 in terms of t1:
t2=αβt1
Step 4: Substitute t2 into Total Time Equation
Substituting t2 into the total time equation:
t1+αβt1=t
t1(1+αβ)=t
t1=βtα+β
Step 5: Find t2
Now substitute t1 back to find t2:
t2=αβt1=αβ⋅βtα+β=αtα+β
Step 6: Calculate Total Distance
The total distance D can be calculated as the sum of the distance covered during acceleration and deceleration.
1. Distance during acceleration:
D1=12αt21=12α(βtα+β)2=αβ2t22(α+β)2
2. Distance during deceleration:
D2=vmaxt2−12βt22
Substituting vmax and t2:
D2=αt1⋅αtα+β−12β(αtα+β)2
D2=α2βtα+β−12β⋅α2t2(α+β)2
Step 7: Combine Distances
Now, combine D1 and D2:
D=D1+D2=αβ2t22(α+β)2+(α2βtα+β−12β⋅α2t2(α+β)2)
After simplification:
D=αβt22(α+β)
Step 8: Find Maximum Velocity
Substituting t1 back into the expression for maximum velocity:
vmax=αt1=α⋅βtα+β=αβtα+β
Final Results
- Total Distance D=αβt22(α+β)
- Maximum Velocity vmax=αβtα+β
Let:
- α = acceleration of the car
- β = deceleration of the car
- t = total time of travel
- t1 = time of acceleration
- t2 = time of deceleration
- vmax = maximum velocity reached
Since the car accelerates for time t1 and decelerates for time t2, we have:
t1+t2=t
During acceleration, the maximum velocity vmax can be expressed as:
vmax=αt1
0=vmax−βt2⟹vmax=βt2
αt1=βt2
t2=αβt1
Substituting t2 into the total time equation:
t1+αβt1=t
t1(1+αβ)=t
t1=βtα+β
Now substitute t1 back to find t2:
t2=αβt1=αβ⋅βtα+β=αtα+β
The total distance D can be calculated as the sum of the distance covered during acceleration and deceleration.
D1=12αt21=12α(βtα+β)2=αβ2t22(α+β)2
D2=vmaxt2−12βt22
Substituting vmax and t2:
D2=αt1⋅αtα+β−12β(αtα+β)2
D2=α2βtα+β−12β⋅α2t2(α+β)2
Now, combine D1 and D2:
D=D1+D2=αβ2t22(α+β)2+(α2βtα+β−12β⋅α2t2(α+β)2)
D=αβt22(α+β)
Substituting t1 back into the expression for maximum velocity:
vmax=αt1=α⋅βtα+β=αβtα+β
- Total Distance D=αβt22(α+β)
- Maximum Velocity vmax=αβtα+β
Topper's Solved these Questions
Similar Questions
A car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t seconds. Then evalute (a) the maximum velocity reached and (b) the total distance travelled.
View SolutionA car acceleration form rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t evaluate (a) the maximum velocity attained and (b) the total distance travelled.
View Solution
Knowledge Check
- Question 1 - Select One
A car accelerates from rest at a constant rate α for sometime , after which it decelerates at a constant rate β and comes to rest. If T is the total time elapsed, the maximum velocity acquired by the car is
A(αβα+β)TB((α+βαβ)TC(α2+β2αβ)TD12αTβ - Question 2 - Select One
A car accelerates from rest at a constant rate for some time after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t, the maximum velocity acquired by the car is given by :
Aαβα+βtBα+βαβtCα2+β2βαDα+β2βα - Question 3 - Select One
A car accelerates from rest at a constant rate for some time after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t, the maximum velocity acquired by the car is given by :
Aab(a+b)tBab(a−b)tCat2(a+b)Dtb2(a+b)
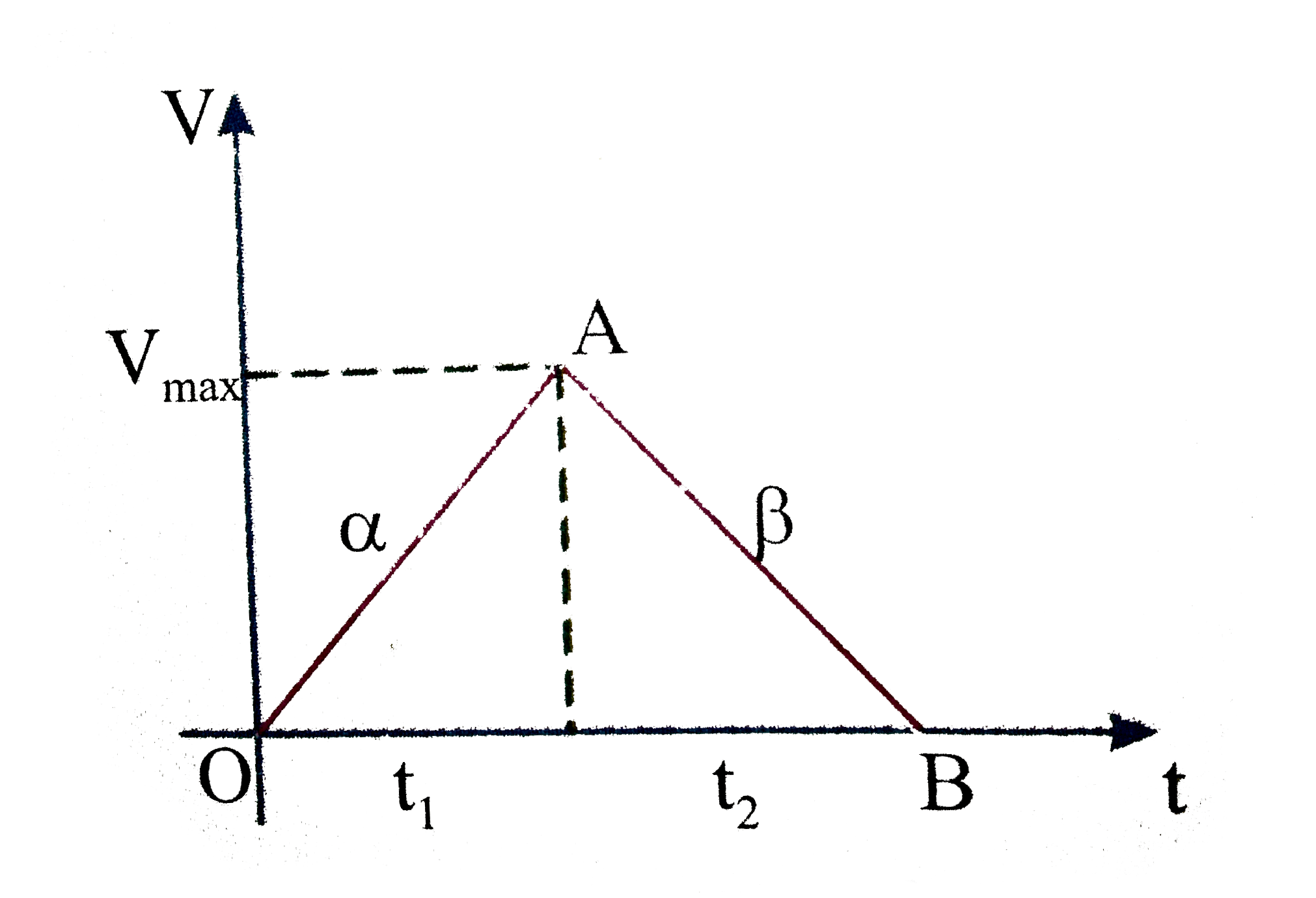
A bus accelerated from rest at a constant rate α for some time, after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t seconds. Then evaluate following parameters from the given graph
(a) the maximum velocity achieved.
(b) the total distance travelled graphically and
(c) Average velocity.View SolutionA particle accelerates from rest at a constant rate for some time and attains a velocity of 8 m/sec. Afterwards it decelerates with the constant rate and comes to rest. If the total time taken is 4 sec, the distance travelled is
View SolutionA car accelerates from rest at a constant rate of 2ms−2 for some time. The it retatds at a constant rate of 4ms−2 and comes to rest. It remains in motion for 6s.
View SolutionA car accelerates from rest at a constant rate of 2ms−2 for some time. Then, it retards at a constant rete of 4ms−2 and comes and rest. If the total time for which it remains in motion is 3 s, Then the total distance travelled is
View SolutionA car accelerates from rest at constant rate of 2ms−2 for some time. Then it retards at a constant rate of 4ms−2 and comes to rest. It remains in motion for 3 seconds
View Solution

