A car is moving with uniform acceleration along a straight line between two stops X and Y. Its speed at X and Y are 2ms−1and14ms−1 , Then
its speed at mid-point of XY is 10ms−1
its speed at a point A such that XA:AY=1:3 is 5ms−1
the time to go from X to the mid-point of XY is double of that to go from mid-point to Y
the distance travelled in first half of the total time is half of the distance travelled in the second half of the time
The correct Answer is:A, C
To solve the problem step by step, we will analyze the motion of the car between points X and Y, where the speeds at these points are given as 2 m/s and 14 m/s respectively.
Step 1: Understand the motion
The car is moving with uniform acceleration from point X to point Y. The initial speed (u) at point X is 2 m/s, and the final speed (v) at point Y is 14 m/s.
Step 2: Use the equations of motion
We can use the third equation of motion:
v2=u2+2as
Where:
- v=14m/s
- u=2m/s
- a is the acceleration
- s is the distance between points X and Y
Rearranging the equation gives:
142=22+2as
196=4+2as
192=2as
as=96(Equation 1)
Step 3: Find the speed at the midpoint
Let’s denote the speed at the midpoint (P) as vp. We can apply the same equation of motion for the distance from X to P and from P to Y.
1. From X to P:
v2p=u2+2as1
Where s1 is the distance from X to P. Since the total distance is s, we have s1=s2.
Thus,
v2p=22+2a(s2)
v2p=4+as(Equation 2)
2. From P to Y:
142=v2p+2as2
Where s2=s2.
Thus,
196=v2p+2a(s2)
196=v2p+as(Equation 3)
Step 4: Set Equations 2 and 3 equal
From Equation 2 and Equation 3:
v2p+as=196
Substituting as from Equation 1:
v2p+96=196
v2p=100
vp=10m/s
Step 5: Analyze the options
1. The speed at the midpoint is 10 m/s.
2. The ratio of distances xA:yA=1:3 can be analyzed using similar equations.
3. The time taken to reach the midpoint is double that taken to reach Y from the midpoint.
Conclusion
After analyzing the options based on the calculations:
- The speed at the midpoint is indeed 10 m/s.
- The ratio of distances can be verified with further calculations.
- The time taken from X to midpoint is double that from midpoint to Y.
The car is moving with uniform acceleration from point X to point Y. The initial speed (u) at point X is 2 m/s, and the final speed (v) at point Y is 14 m/s.
We can use the third equation of motion:
v2=u2+2as
Where:
- v=14m/s
- u=2m/s
- a is the acceleration
- s is the distance between points X and Y
142=22+2as
196=4+2as
192=2as
as=96(Equation 1)
Let’s denote the speed at the midpoint (P) as vp. We can apply the same equation of motion for the distance from X to P and from P to Y.
v2p=u2+2as1
Where s1 is the distance from X to P. Since the total distance is s, we have s1=s2.
v2p=22+2a(s2)
v2p=4+as(Equation 2)
142=v2p+2as2
Where s2=s2.
196=v2p+2a(s2)
196=v2p+as(Equation 3)
From Equation 2 and Equation 3:
v2p+as=196
Substituting as from Equation 1:
v2p+96=196
v2p=100
vp=10m/s
1. The speed at the midpoint is 10 m/s.
2. The ratio of distances xA:yA=1:3 can be analyzed using similar equations.
3. The time taken to reach the midpoint is double that taken to reach Y from the midpoint.
After analyzing the options based on the calculations:
- The speed at the midpoint is indeed 10 m/s.
- The ratio of distances can be verified with further calculations.
- The time taken from X to midpoint is double that from midpoint to Y.
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Comprehension
7 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Subjective Questions
24 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Subjective
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
For a body moving with uniform acceleration along straight line, the variation of its velocity (v) with position (x) is best represented by
View SolutionA car is moving in a straight line with speed 18 km h−1 . It is stopped in 5 s by applying the brakes. Find the speed of car in ms−1 .
View SolutionA car is moving in a straight line with speed 18 km h−1 . It is stopped in 5 s by applying the brakes. Find the retardation
View SolutionA car A is moving with speed 40 km h−1 along a straight line 30∘ north of east and another car B is moving with same speed along a straight line 30∘ south of east. The relative velocity of car A as observed from the car B is
View SolutionA particle moves along straight line for 10 second with unifrom acceleration, a=2ms−2 . Then for next 10 second moves with acceleration, a=4ms−1. The total displacement of particle would be (initial velocity of particle is zero)
View SolutionA car is moving with speed of 2ms−1 on a circular path of radius 1 m and its speed is increasing at the rate of 3ms(−1) The net acceleration of the car at this moment in m/s2 is
View SolutionA car is moving with a speed of 30 ms−1 on a circular path of radius 500 m. If its speed is increasing at the rate of 2 ms−2 , the net acceleration of the car is
View SolutionA car is moving with speed 20ms−1 on a circular path of radius 100 m. Its speed is increasing at a rate of 3ms−2 . The magnitude of the acceleration of the car at that moment is
View SolutionA car is moving with speed 20ms−1 on a circular path of radius 100 m. Its speed is increasing at a rate of 3ms−2 . The magnitude of the acceleration of the car at that moment is
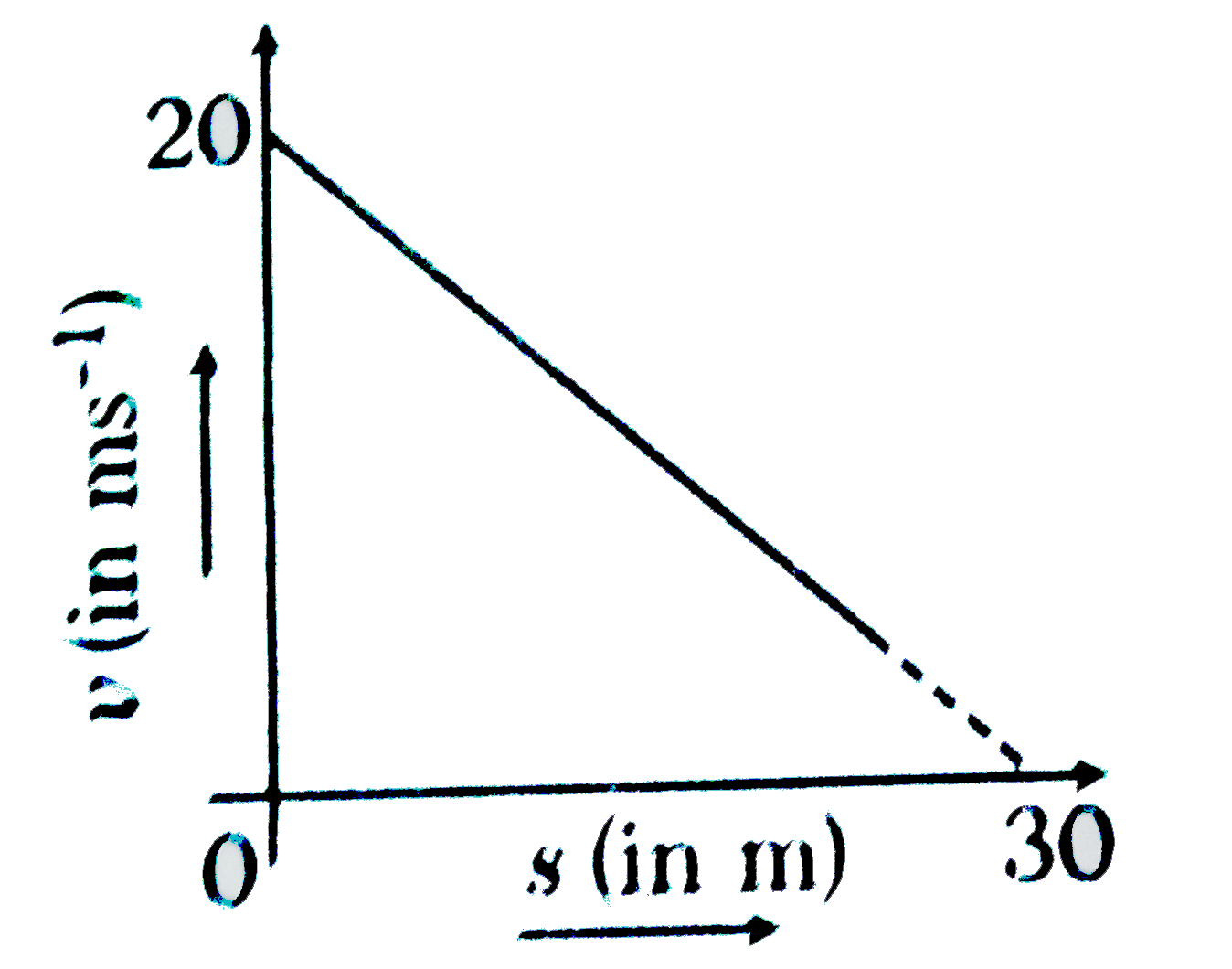
View SolutionIf the velocity v of particle moving along a straight line decreases linearly with its displacement s from 20ms−1 to a value approaching zero at s = 30 m, then acceleration of the particle at v=10ms^(-1) is
View Solution
