For a body moving with uniform acceleration along straight line, the variation of its velocity (v) with position (x) is best represented by
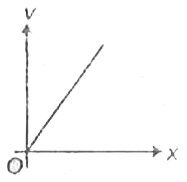
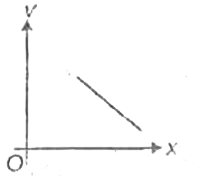
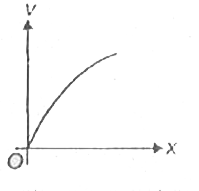
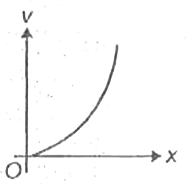
The correct Answer is:C
To solve the problem of how the velocity (v) of a body moving with uniform acceleration varies with its position (x), we can follow these steps:
1. Understanding the Problem:
We are dealing with a body moving with uniform acceleration along a straight line. This means that the acceleration (a) is constant.
2. Using the Relationship Between Acceleration, Velocity, and Position:
We know that acceleration can be expressed in two ways:
- a=dvdt (acceleration as the rate of change of velocity with respect to time)
- a=vdvdx (acceleration as the product of velocity and the rate of change of velocity with respect to position)
3. Setting Up the Equation:
Since the acceleration is constant, we can set:
a=vdvdx=c
where c is a constant representing the uniform acceleration.
4. Rearranging the Equation:
Rearranging gives us:
vdv=cdx
5. Integrating Both Sides:
We integrate both sides:
∫vdv=∫cdx
This results in:
v22=cx+C
where C is the integration constant.
6. Determining the Constant:
To find the constant C, we can use initial conditions. If at x=0, v=0:
022=c(0)+C⟹C=0
Thus, the equation simplifies to:
v22=cx
or
v2=2cx
7. Final Form of the Equation:
Rearranging gives us:
v2=2cx
This equation shows that the relationship between v2 and x is linear, which is characteristic of a parabolic graph.
8. Identifying the Graph:
The equation v2=2cx resembles the standard form of a parabola y=kx where y is v2 and x is the position x. Therefore, the graph of v versus x is a parabola opening to the right.
Conclusion:
The variation of velocity (v) with position (x) for a body moving with uniform acceleration is best represented by a parabolic curve.
We are dealing with a body moving with uniform acceleration along a straight line. This means that the acceleration (a) is constant.
We know that acceleration can be expressed in two ways:
- a=dvdt (acceleration as the rate of change of velocity with respect to time)
- a=vdvdx (acceleration as the product of velocity and the rate of change of velocity with respect to position)
Since the acceleration is constant, we can set:
a=vdvdx=c
where c is a constant representing the uniform acceleration.
Rearranging gives us:
vdv=cdx
We integrate both sides:
∫vdv=∫cdx
This results in:
v22=cx+C
where C is the integration constant.
To find the constant C, we can use initial conditions. If at x=0, v=0:
022=c(0)+C⟹C=0
Thus, the equation simplifies to:
v22=cx
or
v2=2cx
Rearranging gives us:
v2=2cx
This equation shows that the relationship between v2 and x is linear, which is characteristic of a parabolic graph.
The equation v2=2cx resembles the standard form of a parabola y=kx where y is v2 and x is the position x. Therefore, the graph of v versus x is a parabola opening to the right.
The variation of velocity (v) with position (x) for a body moving with uniform acceleration is best represented by a parabolic curve.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - B)
33 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - C)
36 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - EXERCISE
29 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -J (Aakash Challengers Questions)
7 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - J)
2 Videos
Similar Questions
A body starting from rest moves along a straight line with a constant acceleration. The variation of speed (v) with distance (s) is represented by the graph:
View SolutionA body moving with uniform acceleration a straight line describes 25m in the fifth second and 33m in the seventh second. Find its initial velocity and acceleration.
View SolutionA particle moving with uniform acceleration from A to B along a straight line has velcities v1 and v2 at A and B respectively. If C is the mid-point between A and B then determine the velocity of the particle at C .
 .
.
View SolutionA body is moving with variable acceleartion (a) along a straight line. The average acceleration of body in time interval t1 to t2 is :-
View SolutionA particle moving with a uniform acceleration along a straight line covers distances a and b in successive intervals of p and q second. The acceleration of the particle is
View SolutionFor a body travelling with uniform acceleration, its final velocity is v=√180−7x , where x is the distance travelled by the body. Then the acceleration is
View SolutionA car is moving with uniform acceleration along a straight line between two stops X and Y. Its speed at X and Y are 2ms−1and14ms−1 , Then
View SolutionWhen a body is subjected to a uniform acceleration, it always moves in a straight line.
Straight line motion is the natural tendency of the body.
View SolutionVelocity of a body moving a straight line with uniform acceleration (a) reduces by 34 of its initial velocity in time t0. The total time of motion of the body till its velocity becomes zero is
View SolutionA particle starts with some initial velocity with an acceleration along the direction of motion. Draw a graph depicting the variation of velocity (v) along y-axis with the variation of displacement(s) along x-axis.
View Solution
