A car moves in a straight line, the car accelerates from rest with a constant acceleraation α on a straight foad. After gaining a velocity v, the car moves with that velocity for somerime. Then car decelerates with a retardation β, If the total distance covered by the car is equal to s find the total time of its motion.
The correct Answer is:sv+v2(1(α)+1β
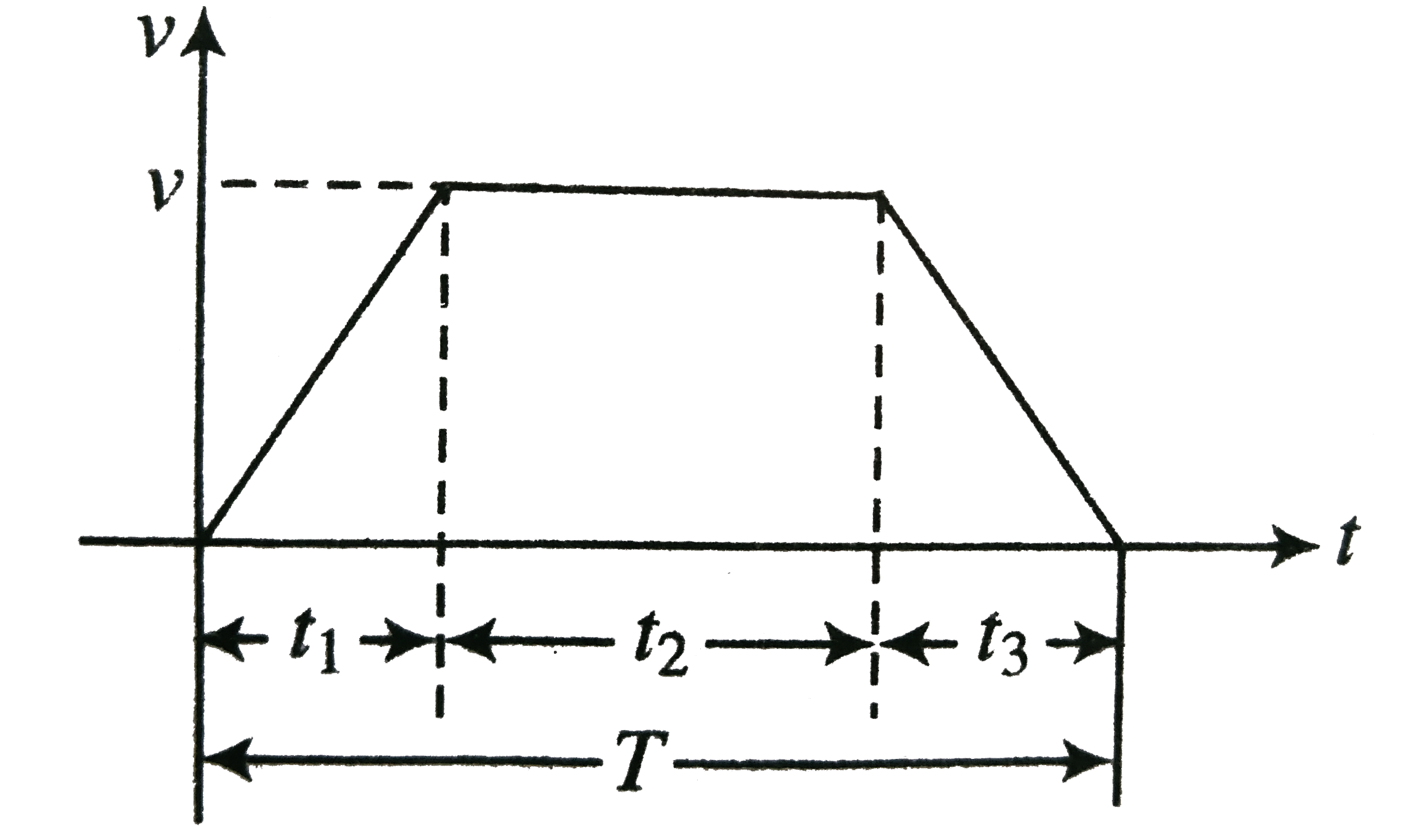
Let the car accelerate for a time t1. Move uniformly for a time t2 and then retard for a time t3as shown in the v−t graph.
 .
.
Then the total time T of the car is
T=t1+t2+t3 (i)
The slope of v−t graph
gives vt1=α and −vt3=−β
Then t1+t3=vβ (ii)
Area under v−t graph gives the total displacement
s=Area of the trapezinum =v2(t2+T)
This gives t2=2sv−T (iii)
Substituting t1+t3 from Eq. (ii) and t2 From Eq. (iii) in Eq. (i) we
have T=vα+vβ−2sv−T
This yields T=sv+v2(1α+1β).
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Single Correct
52 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Graphical Concept
17 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.4
16 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Video
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
A motor car, starting from rest, moves with uniform acceleration and attains a velocity of 8ms−1 in 8 s. It then moves with uniform velocity and finally brought to rest in 32 m under unifrom retardation. The total distance covered by the car is 464 m. Find the total time taken.
View SolutionA motor car, starting from rest, moves with uniform acceleration and attains a velocity of 8ms−1 in 8 s. It then moves with uniform velocity and finally brought to rest in 32 m under unifrom retardation. The total distance covered by the car is 464 m. Find the retardation
View Solution
Knowledge Check
A car accelerates from rest at a constant rate α for sometime , after which it decelerates at a constant rate β and comes to rest. If T is the total time elapsed, the maximum velocity acquired by the car is
A(αβα+β)TB((α+βαβ)TC(α2+β2αβ)TD12αTβA constant power P is applied to a car starting from rest. If v is the velocity of the car at time t, then:
Av∝tBv∝1tCv∝√tDv∝1√t
A motor car, starting from rest, moves with uniform acceleration and attains a velocity of 8ms−1 in 8 s. It then moves with uniform velocity and finally brought to rest in 32 m under unifrom retardation. The total distance covered by the car is 464 m. Find the acceleration.
View SolutionA motor car, starting from rest, moves with uniform acceleration and attains a velocity of 8ms−1 in 8 s. It then move with uniform velocity and finally brought to rest in 32 m under uniform retardation. The total distance covered by the car is 646 m. Find (i) the acceleration (ii) the retardation and (iii) the total time taken.
View SolutionA car starts from rest and accelerates uniformly for 20 seconds to a velocity of 72 kmh–1. It then runs at constant velocity and finally brought to rest in 200 m with a constant retardation. The total distance covered is 600 m. Find the acceleration, retardation and the total time taken.
View SolutionA car starts form rest and accelerates uniformly for 10s to a velocity of 8ms−1. It then runs at a constant velocity an dis finally brought to rest in 64m with a constant retardation. The total distance covered by the car is 584m Find the value of acceleration, retardation, and total time taken.
View SolutionA car acceleration form rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t evaluate (a) the maximum velocity attained and (b) the total distance travelled.
View SolutionA car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β and ultimately comes to rest.If the total time-lapse is t, what is the total distance described and maximum velocity reached ?
View Solution
