A car of mass 1000g is brought to rest from a speed of 40ms−1 in a distance of 80m. Find the braking force of the car assuming that it is constant and that there is a constant resistance of motion of 100N
To solve the problem step by step, we will follow the physics principles related to forces, motion, and kinematics.
1. Identify Given Data:
- Mass of the car (m) = 1000 g = 1 kg (since 1000 g = 1 kg)
- Initial speed (u) = 40 m/s
- Final speed (v) = 0 m/s (the car is brought to rest)
- Distance (s) = 80 m
- Constant resistance (F_r) = 100 N
2. Use the Kinematic Equation:
We can use the kinematic equation that relates initial velocity, final velocity, acceleration, and distance:
v2=u2+2as
Substituting the known values:
0=(40)2+2a(80)
This simplifies to:
0=1600+160a
Rearranging gives:
160a=−1600⇒a=−10m/s2
(The negative sign indicates deceleration.)
3. Apply Newton's Second Law:
According to Newton's second law, the net force acting on the car is equal to the mass of the car multiplied by its acceleration:
Fnet=ma
The net force can be expressed as the difference between the braking force (F_B) and the resistance force (F_r):
Fnet=FB−Fr
Substituting the known values:
ma=FB−Fr
1000×(−10)=FB−100
This simplifies to:
−10000=FB−100
4. Solve for the Braking Force (F_B):
Rearranging the equation to solve for F_B:
FB=−10000+100
FB=−9900N
Since force is a vector quantity, we can express the magnitude as:
FB=9900N
Final Answer:
The braking force of the car is 9900 N.
- Mass of the car (m) = 1000 g = 1 kg (since 1000 g = 1 kg)
- Initial speed (u) = 40 m/s
- Final speed (v) = 0 m/s (the car is brought to rest)
- Distance (s) = 80 m
- Constant resistance (F_r) = 100 N
We can use the kinematic equation that relates initial velocity, final velocity, acceleration, and distance:
v2=u2+2as
Substituting the known values:
0=(40)2+2a(80)
This simplifies to:
0=1600+160a
Rearranging gives:
160a=−1600⇒a=−10m/s2
(The negative sign indicates deceleration.)
According to Newton's second law, the net force acting on the car is equal to the mass of the car multiplied by its acceleration:
Fnet=ma
The net force can be expressed as the difference between the braking force (F_B) and the resistance force (F_r):
Fnet=FB−Fr
Substituting the known values:
ma=FB−Fr
1000×(−10)=FB−100
This simplifies to:
−10000=FB−100
Rearranging the equation to solve for F_B:
FB=−10000+100
FB=−9900N
Since force is a vector quantity, we can express the magnitude as:
FB=9900N
The braking force of the car is 9900 N.
Topper's Solved these Questions
- FORCE AND LAWS OF MOTIONBOOK - MTG IIT JEE FOUNDATIONCHAPTER - FORCE AND LAWS OF MOTIONEXERCISE - EXERCISE (LONG ANSWER TYPE)
9 Videos
- FORCE AND LAWS OF MOTIONBOOK - MTG IIT JEE FOUNDATIONCHAPTER - FORCE AND LAWS OF MOTIONEXERCISE - EXERCISE (INTEGER VALUE TYPE )
5 Videos
- FORCE AND LAWS OF MOTIONBOOK - MTG IIT JEE FOUNDATIONCHAPTER - FORCE AND LAWS OF MOTIONEXERCISE - EXERCISE (VERY SHORT ANSWER QUESTION)
15 Videos
- FOOTSTEPS TOWARDS NEETBOOK - MTG IIT JEE FOUNDATIONCHAPTER - FOOTSTEPS TOWARDS NEETEXERCISE - Multiple Choice Question
45 Videos
- GRAVITATION BOOK - MTG IIT JEE FOUNDATIONCHAPTER - GRAVITATION EXERCISE - Olympiad/HOTS Corner
20 Videos
Similar Questions
A car starts from rest and accelerates uniformly to a speed 50ms^(-1) over a distance of 250m . Find the acceleration and time taken by the car to cover this distance.
View SolutionA long a straight road, a car moving with a speed of 130 km/h is brought to a stop in a distance of 210 m. (a) Find the magnitude of the deceleration of the car ( assumed uniform ). (b) How long does it take for the car to stop ?
View Solution
Knowledge Check
A car of mass =m=1000kg is moving with constant speed v=100m/s on a parabolic shaped bridge AFOE of span force applied by the bridge on the car when he car is at point E, is:
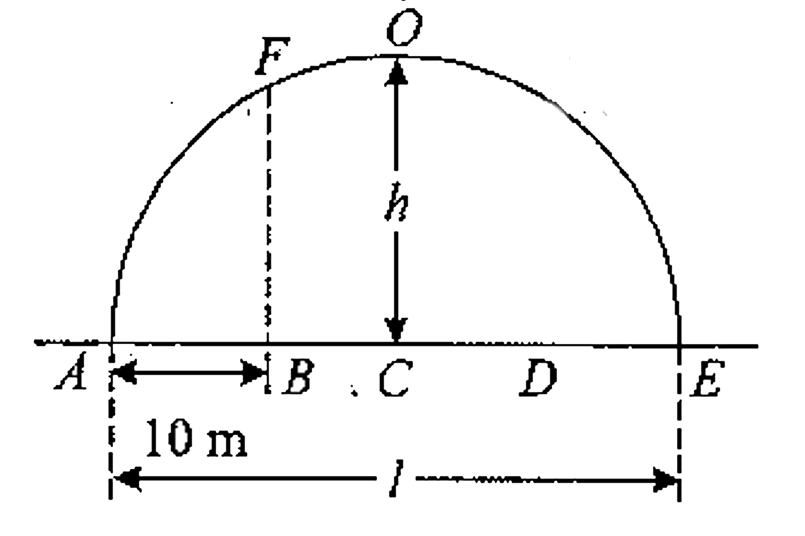 A5000√52NB5000√2NC10000√2ND5000√25N
A5000√52NB5000√2NC10000√2ND5000√25N
A bullet of mass 50g moving with a speed of 500ms−1 is brought to rest in 0.01s Find the impulse and the average force .
View SolutionA car of mass 1000 kg is moving with a certain speed when a constant braking force 1000 N acts on it for 5s and the speed of the car reduces to half its original speed. Find the further time required to stop the car if the same constant force acts.
View SolutionA car of mass 1000 kg is moving with a certain speed when a constant braking force 1000 N acts on it for 5s and the speed of the car reduces to half its original speed. Find the further time required to stop the car if the same constant force acts.
View SolutionA car of mass 800 kg is moving with a constant velocity 40 km/h. Find the net force on it.
View SolutionA car of mass 800 kg is moving with a constant velocity 40 km/h . Find the net force on it.
View SolutionA car moving aling a straight highway with speed of 126kmh−1 is brought to a stop within a distance of 200m. What is the retardation of the car (assumed uniform ) ans how doest it take fro the car to stop ?
View SolutionA car moving along a straight highway with speed of 126 km h−1 is brought to a stop within a distance of 200 m. What is the retardation of the car (assumed uniform) and how long does it take for the car to stop ?
View Solution
