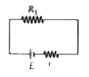
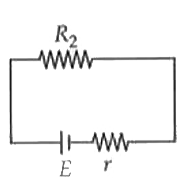
A cell of e.m.f E is connected to a resistance R1 for time i and the amount of heat generated in it is H. If the resistance R1 is replaced by another resistance R2 and is connected to the cell for the same time i, the amount of heat generated in R2 is 4H. Then the internal resistance of the cell is
2R1+R22
√R1R22√R2−√R1√R2−2√R1
√R1R2√R2−2√R12√R2−√R1
√R1R2√R2−2√R12√R2+√R1
The correct Answer is:B
Let r be internal resistance of the cell. For the first case, the amount of heat R generated in resistance R1 in a time t is
H=E2R1(R1+r2)t
orE2=H(R1+r)2R−1t
for second cae the amount of heat generated in R2 in the same time t is
4H=E2R2t(R2+r)2orE2=4H(R2+r)2R2t
equating (i) and (ii ) we get
H(R1+r)2r1t=4H(R2+r)2R2t
(R1+r)2R1=4(R2+r)2R2or(R1+r)√R1=2(R2+r)√R2
⇒√R2(R1+r)=2√R1(R2+r)
⇒√R2R1+√R2r=2√R1R2+2√R1r
⇒√R2r−2√R1r=2√R1R2−√R2R1
⇒r(√R2−2√R1)=√R1R2[2√R2−√R1]
⇒r=√R1R22√R2−√R1√R2−2√R1
Topper's Solved these Questions
- BULK PROPERTIES OF MATTERBook:MTG-WBJEEChapter:BULK PROPERTIES OF MATTERExercise:WB JEE PREVIOUS YEARS QUESTIONS (ONE OR MORE THAN ONE OPTION CORRECT TYPE)
Explore 1 Video
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT Book:MTG-WBJEEChapter:ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENT Exercise:WB JEE Previous Years Questions
Explore 14 Videos
Similar Questions
A cell sends a current through a resistance R1 for time t, next the same cell sends current through another resistance R2 for the time t If the same amount of heat is developed in both the resistance then find the internal resistance of the cell
View SolutionA cell sends a current through a resistance R1 for time t, next the same cell sends current through another resistance R2 for the time t If the same amount of heat is developed in both the resistance then find the internal resistance of the cell
View Solution
Knowledge Check
A cell of constant e.m.f. first connected to a resistance R1 and then connected to a resistance R2. If power delivered in both cases is then the internal resistance o f the cell is
A√R1R2B√R1/R2CR1−R22DR1+R22A cell of constant emf first connected to a resistance R1 and then connected to resistance R2. If power deliverd in both cases is same, then the internal resistance of the cell is
A√R1R2B√R1R2CR1−R22DR1+R22A cell of constant e.m.f. first connected to a resistance R1 and then connected to a resistance R2. If power delivered in both cases is then the internal resistance o f the cell is
A√R1+R2B√R1R2CR1−R22DR1+R22
If a cell of constant E.M.F. produces the same amount of the heat during the same time in two independent resistors R1 and R2, when they are separately connected across the terminals of the cell, one after the another, find the internal resistance of the cell.
View Solution5When a cell of emf E and internal resistance r, is connected to the ends of a resistance R, then current through resistance is I. If the same cell is connected to the ends of a resistance R/2 then the current would be-
View SolutionA cell of e.m.f. E is connected with an external resistance R , then p.d. across cell is V . The internal resistance of cell will be
View SolutionA cell of emf (E) and internal resistance (r) is balanced across (l) length of potentiometer wire. If another cell of emf 2E and internal resistance (2r) is connected in parallel to the first cell , then the balancing length will be
View SolutionA battery of emf E and internal resistance r is connected to a resistor of restance r1 and Q Joules of heat is produced in a certain time t. When te same battery is connected to another resistor of resistance r2 the same quantity of heat is produced in the same time t. Then the value of r is
View Solution
