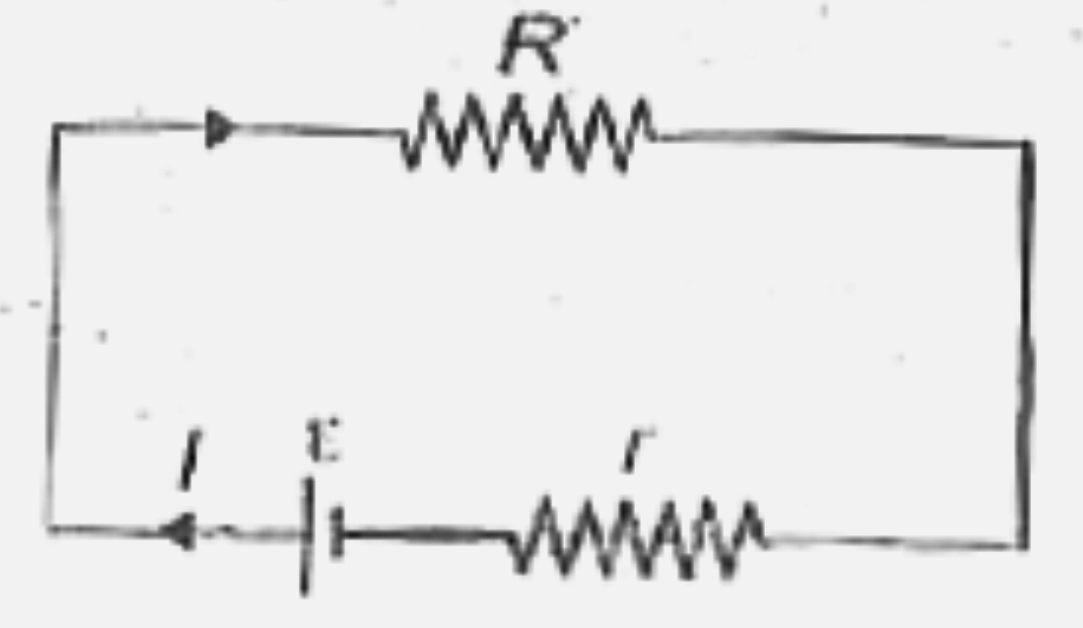
A cell of internal resistances r is connected to a load of resistance R . Energy is dissipated in the load, but some thermal energy is also wasted in the cell. The efficiency of such an arrangement is found from the expression
( Energy dissipated in the load )/( Energy dissipated in the complete circuit)
Which of the following gives the efficiency in this case?
rR
Rr
rR+r
RR+r
The correct Answer is:D
To solve the problem, we need to determine the efficiency of a circuit consisting of a cell with internal resistance r connected to a load with resistance R. The efficiency is given by the ratio of the energy dissipated in the load to the total energy dissipated in the entire circuit.
1. Understanding the Circuit:
- We have a cell with an electromotive force (emf) E and an internal resistance r.
- The load resistance is R.
- The total resistance in the circuit is R+r.
2. Calculating the Current:
- The current I flowing through the circuit can be calculated using Ohm's law:
I=ER+r
3. Energy Dissipated in the Load:
- The energy dissipated in the load HR can be calculated using the formula for power (which is energy per unit time) and the relationship P=I2R:
HR=I2R
- Substituting the expression for I:
HR=(ER+r)2R=E2R(R+r)2
4. Calculating Total Energy Dissipated in the Circuit:
- The total energy dissipated HT in the circuit includes the energy dissipated in both the load and the internal resistance:
HT=HR+Hr
- The energy dissipated in the internal resistance Hr is given by:
Hr=I2r=(ER+r)2r=E2r(R+r)2
- Therefore, the total energy dissipated in the circuit is:
HT=HR+Hr=E2R(R+r)2+E2r(R+r)2=E2(R+r)(R+r)2
5. Calculating Efficiency:
- The efficiency η is defined as the ratio of the energy dissipated in the load to the total energy dissipated in the circuit:
η=HRHT
- Substituting the expressions for HR and HT:
η=E2R(R+r)2E2(R+r)(R+r)2=RR+r
6. Final Result:
- Thus, the efficiency of the arrangement is given by:
η=RR+r
Conclusion:
The efficiency of the circuit arrangement is RR+r.
- We have a cell with an electromotive force (emf) E and an internal resistance r.
- The load resistance is R.
- The total resistance in the circuit is R+r.
- The current I flowing through the circuit can be calculated using Ohm's law:
I=ER+r
- The energy dissipated in the load HR can be calculated using the formula for power (which is energy per unit time) and the relationship P=I2R:
HR=I2R
- Substituting the expression for I:
HR=(ER+r)2R=E2R(R+r)2
- The total energy dissipated HT in the circuit includes the energy dissipated in both the load and the internal resistance:
HT=HR+Hr
- The energy dissipated in the internal resistance Hr is given by:
Hr=I2r=(ER+r)2r=E2r(R+r)2
- Therefore, the total energy dissipated in the circuit is:
HT=HR+Hr=E2R(R+r)2+E2r(R+r)2=E2(R+r)(R+r)2
- The efficiency η is defined as the ratio of the energy dissipated in the load to the total energy dissipated in the circuit:
η=HRHT
- Substituting the expressions for HR and HT:
η=E2R(R+r)2E2(R+r)(R+r)2=RR+r
- Thus, the efficiency of the arrangement is given by:
η=RR+r
The efficiency of the circuit arrangement is RR+r.
Topper's Solved these Questions
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Multiple Correct
5 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Assertion - Reasoning
6 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Subjective
8 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer Type
4 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
Similar Questions
Knowledge Check
In a circuit a cell with internal resistance r is connected to an external resistance R. The condition for the maximum current that drawn from the cell is
AR=rBR<rCR>rDR=0
A cell of emf ε and internal resistance r is connected across a load resistance R .
(i) Find the maximum power delivered at the load ?
(ii) Draw the power (P) vs load resistance (R) graph .
View SolutionIf a battery of emf E and internal resistance r is connected across a load of resistance R. Shot that the rate at which energy is dissipated in R is maximum when R=r and this maximur power is P=E2/4r.
View SolutionA coil having an inductance L and a resistance R is connected to a battery of emfε. Find the time elapsed before, the magnetic field energy stored in the circuit reaches half its maximum value.
View SolutionAn inducatane L and a resistance R are connected in series with a battery of emf epsilon. Find the maximum rate at which the energy is stored in the magnetic field.
View SolutionA power supply with an e.m.f ε and internal resustance r is connected to a variable resistance R. Find the dependence of the total power generated by the supply and of the power delivered to the external circuit on the load resistance.
View SolutionAn Uncharged capacitor C is connected to a battery through a resistance R. Show that by the time the capacitor gets fully charged, the energy dissipated in R is the same as the energy stored in C.
View SolutionA capacitor of capacitance C is connected to a battery of emf (ε)at t=0 through a resistance R. Find the maximum rate at which energy is stored in the capacitor. When does the rate has this maximum value?
View Solution
