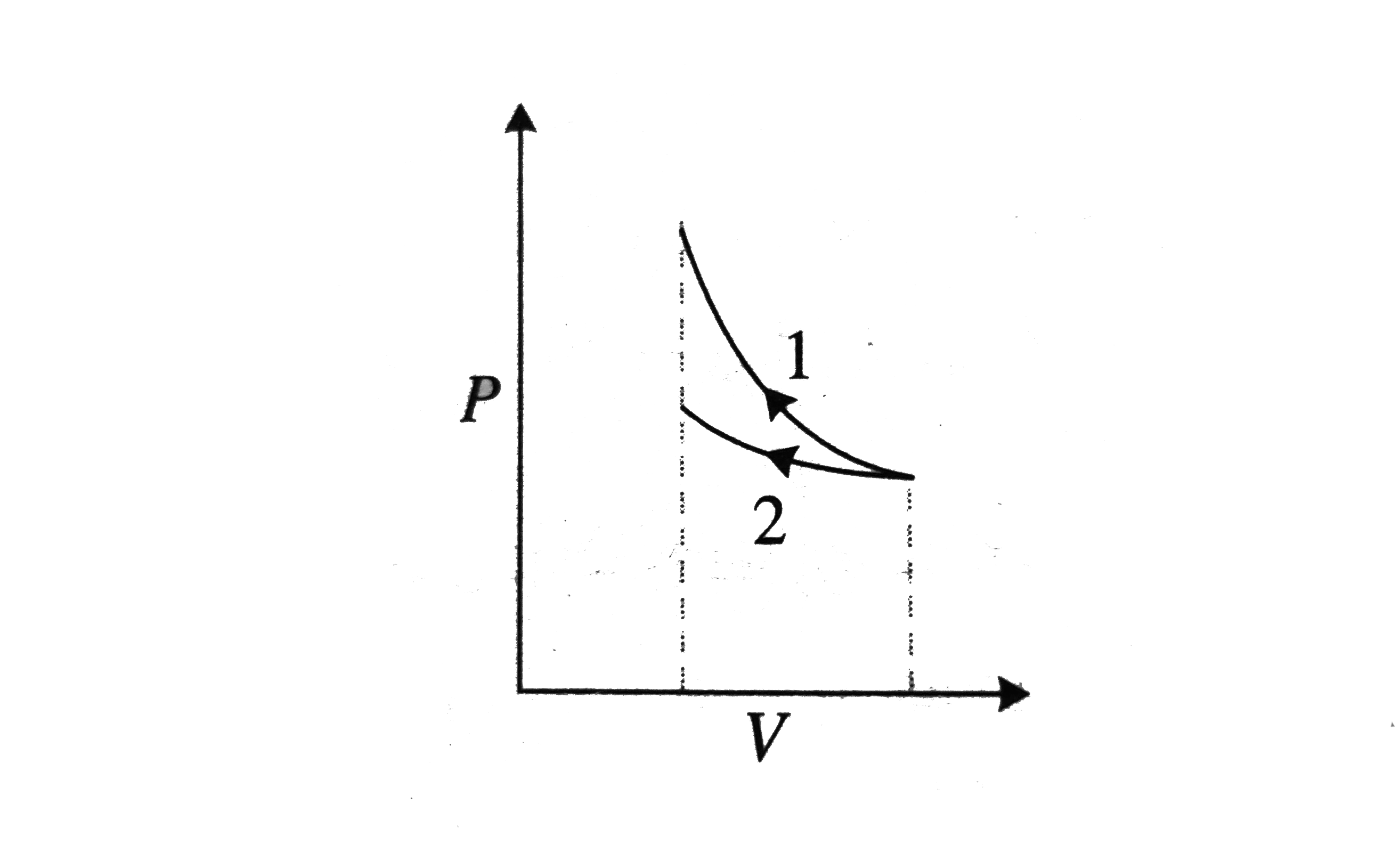
A certain mass of nitrogen was compressed η=5.0 times (in terms of volume), first adiabatically, and then isothermally. In both cases the initial state of the gas was the same. Find the ratio of the respective works expended in each compression.
Let (p0,V0,T0) be the initial state of the gas.
We know Aadia=−vRΔTγ−1 (work done by the gas)
But from the equation TVγ−1= constant, we get ΔT=T0(ηγ−1−1)
Thus Aadia=−vRT0(ηγ−1−)γ−1
On the other hand, we know Aiso=vRT01n(1η)=−vRT01nη (work done by the gas )
Thus AadiaAiso=ηγ−1−1(γ−1)1nη=50.4−10.4×1n5=1.4.
Topper's Solved these Questions
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Kinetic Theory Of Gases
51 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - The Second Law Of Thermodynamics - Entropy
47 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
A gas is first compressed adiabatically and then isothermally. In both cases, the initial state of the gas is the same. Find in which case more work is done on the gas.
View SolutionA certain mass of a gas is compressed first adiabatically, and then isothermally. In both cases, the initial state of the gas is the same. Is the work done W1 in the first case greater than the work done W2 in the second case ? Explain.
View Solution
Knowledge Check
A monatomic gas is suddenly compressed to (18)th of its initial volume adiabatically. The ratio of its final pressure to the initial pressure is (Given, the ratio of the specific heats of the given gas to be 5/3)
A32B40/3C24/5D85.6 liter of helium gas at STP is adiabatically compressed to 0.7 liter. Taking the initial temperature to be T1, the work done in the process is
A98RT1B32RT1C158RT1D92RT1A diatomic ideal gas is compressed adiabatically to 1/32 of its initial volume. If the initial temperature of the gas is Ti (in Kelvin) and the final temperature is a Ti, the value of a is
A4B6C7D8
If a certain mass of gas is made to undergo separately adiabatic and isothermal expansions to the same pressure, starting form the same initial conditions of temperature and pressure, then, as compared to that of isothermal expansion, in the case of adiabatic expansion, the final
View SolutionHelium of mass m=1.7g is expanded adiabatically n=3.0 times and then compressed isobarically down to the initial volume. Find the entropy increment of the gas in this process.
View SolutionA given mass of a gas at 0∘C is compressed reversible and adiabatically to a pressure 20 times the initial value. Calculate the final temperature of the gas. [CPCV=1.42
View SolutionAn ideal gas is compressed at constant pressure of 105Pa until its volume is halved. If the initial volume of the gas as 3.0×10−2m3, find the work done on the gas?
View SolutionA monoatomic gas is suddenly compressed to (1/8)th of initial volume adiabatically . The ratio of its final pressure to the initial volume adiabatically. The ratio of (Given the ratio of the specific heats of the given gas to be 53 )
View Solution
