A chain of mass M and length L is held vertical by fixing its upper end to a rigid support. The tension in the chain at a distance y from the rigid support is:
Mg
(L−xL)Mg
(LL−x)Mg
xLMg
The correct Answer is:B
(b) Tx=mass of rope of length (L−x)×g=ML(L−x)g
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Assertion and reason
28 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Match the columns
7 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.4
20 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
A vertical hanging bar of length l and mass m per unit length carries a load of mass M at lower end, its upper end is clamped to a rigid support.The tensile stress a distance x from support is (A→ area of cross - section of bar)
View SolutionTension in the rope at the rigid support is (g=10m/s2)
View Solution
Knowledge Check
A chain of mass M and length l is held vertically such that its bottom end just touches the surface of a horizontal table. The chain is released from rest. Assume that the portion of chain on the table does not form a heap. The momentum of the portion of the chain above the table after the top end of the chain falls down by a distance l8.
A314M√glB316M√glC716M√glD914M√glA partical of mass m is attached to a massless string of length l and is oscillating in a vrtical plane with the other end of the string fixed to a rigid support. The tension in the string at a certain instant is T=kmg .
Ak can never be geaater than 1Bk can never be less than 1Ck can never be equal than 1Dk can never be geaater than 3A uniform chain of mass M and length L is rotated in a horizontal circle about its one end at an angular frequency ω. The tension at its axis is
AMω2LBMω2L8CMω2L4DMω2L2
A very flexible uniform chain of mass M and length L is suspended vertically so that its lower and just touches the surface of a table. When the upper end of the chain is released it falls with each link coming to rest the instant it strikes the table. Find the force exerted by the chain on the table at the moment when y part of the chain has already rested on the table.
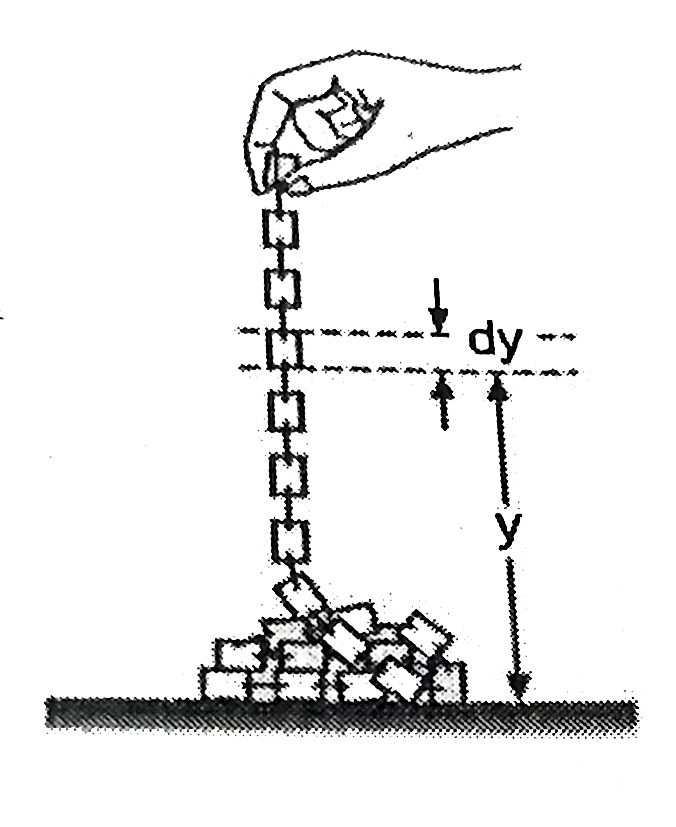
View SolutionA chain with uniform mass per unit length lies in a vertical plane along the slope of a smooth hill. The two end of the chain are at same height. If the chain is released from this position find its acceleration.

View SolutionA stationlay unifrom sting of modlulus Y, density ρ and length 'I' is hanging from a rigid support.
The stress at a distance x from the point of tis suspension.
View SolutionA block of mass m is pulled by a uniform chain of mass m tied to it by applying a force F at the other end of the chain. The tension at a point P which is at a distance of quarter of the length of the chain from the free end, will be
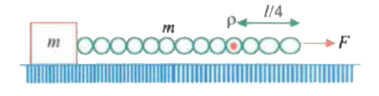
View SolutionA block of mass m is pulled by a uniform chain of mass m tied to it by applying a force F at the other end of the chain.The tension at a point P which is at a distance of quarter of the length of the chain from the free end,will be

View Solution
