A block of mass m is pulled by a uniform chain of mass m tied to it by applying a force F at the other end of the chain. The tension at a point P which is at a distance of quarter of the length of the chain from the free end, will be
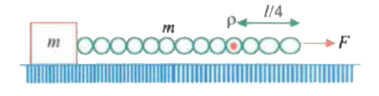
3F4
7F8
6F7
4F5
The correct Answer is:B
a=Fm1+m2,T=(m1+34m2)a
Topper's Solved these Questions
- LAW OF MOTIONBOOK - NARAYNACHAPTER - LAW OF MOTIONEXERCISE - EXERCISE - II (H.W)(MOTION ON A HORIZONTAL ROUGH SURFACE)
12 Videos
- LAW OF MOTIONBOOK - NARAYNACHAPTER - LAW OF MOTIONEXERCISE - EXERCISE - II (H.W)(MOTION OF A BODY ON THE INCLINED PLANE)
9 Videos
- LAW OF MOTIONBOOK - NARAYNACHAPTER - LAW OF MOTIONEXERCISE - EXERCISE - II (H.W)(NEWTON.S LAWS OF MOTION)
9 Videos
- KINETIC THEORY OF GASESBOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)
52 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBOOK - NARAYNACHAPTER - MATHEMATICAL REVIEW & PHYSICAL WORLDEXERCISE - C.U.Q
13 Videos
Similar Questions
A block of mass M is attached to a uniform rope of mass m. This arrangement is pulled by applying a force F at the rope as shown. Find the tension in the rope (a) at the junction of the rope and the block (b) at the mid point of the rope.
View SolutionA block is lying on the horizontal frictionless surface. One end of a uniform rope is fixed to the block which is pulled in the horizontal direction by applying a force F at the other end. If the mass of the rope is half the mass of the block. The tension in the middle of the rope will be
View Solution
Knowledge Check
A block is lying on the horizontal frictionless surface. One end of a uniform rope is fixed to the block which is pulled in the horizontal direction by applying a force F at the other end. If the mass of the rope is half the mass of the block. The tension in the middle of the rope will be
AFB2F/3C3F/5D5F/6A chain of mass M and length L is held vertical by fixing its upper end to a rigid support. The tension in the chain at a distance y from the rigid support is:
AMgBMg(L−y)/LCMgL/(L−y)DMgy/LA string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
AZeroBFCF(L−y)LDF(l−y)M
A chain of mass M and length L is held vertical by fixing its upper end to a rigid support. The tension in the chain at a distance y from the rigid support is:
View SolutionA chain of mass M and length L is held vertical by fixing its upper end to a rigid support. The tension in the chain at a distance y from the rigid support is:
View SolutionA block of mass m is attached to a chain as shown in the diagram. Find the tension in each of the three chains. The ring and chains are light.

View SolutionA chain of length 'L' and mass 'M' is hanging by fixing its upper end to a rigid support. The tension in the chain at a distance 'x' from the rigid support is
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m. If a force F is applied at one end of the rope. Find the force which the rope exerts on the block.
View Solution
