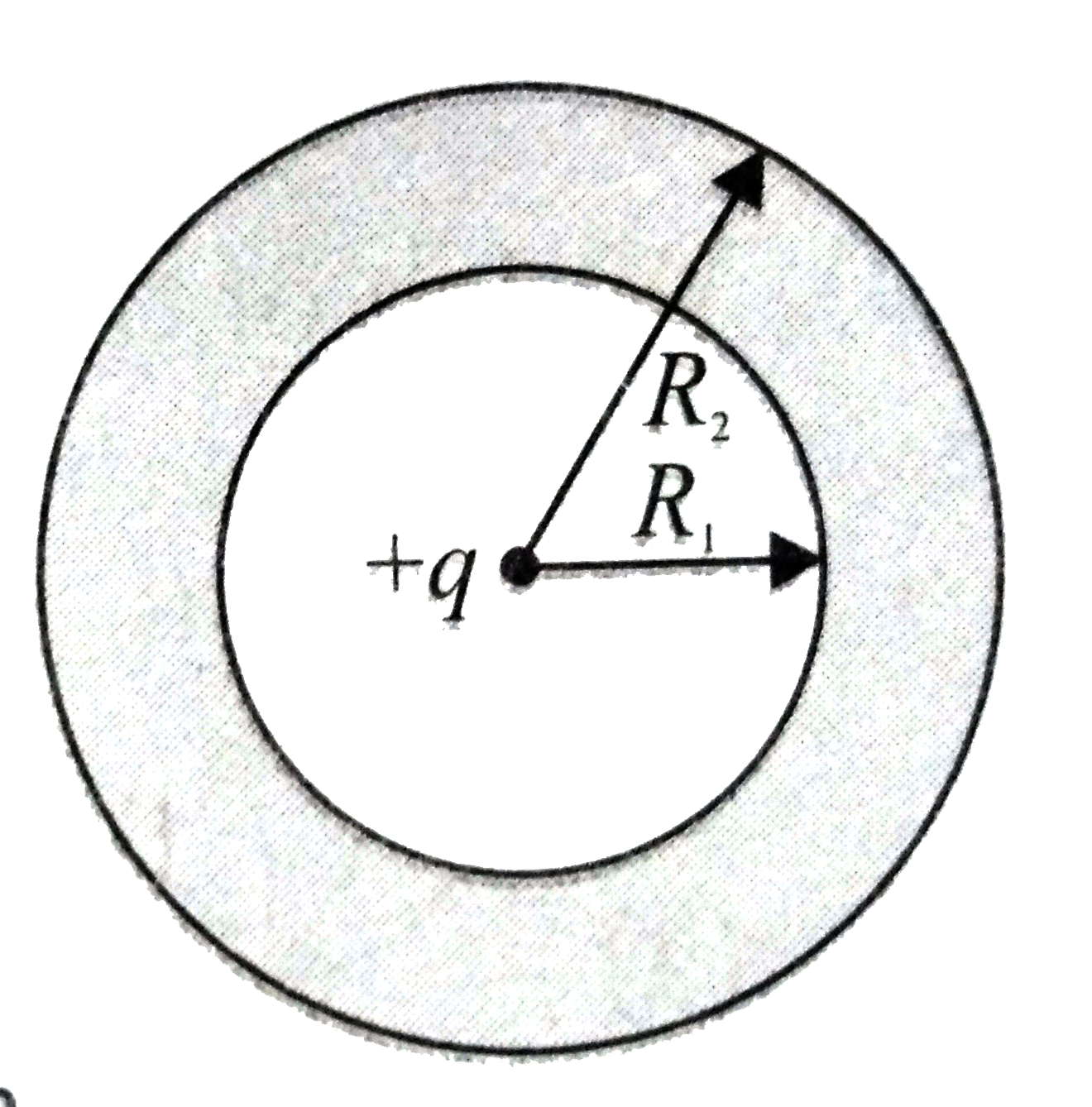
A charge Q is placed at the centre of an uncharged, hollow metallic sphere of radius of rasius alpha. (a) Find the surface charge density on the inner surface and on the outer surface. (b) If a charge q is pur on the sphege, what would be the surface charge dendities on the inner and the outer surface? (c) Find the electric field inside the sphere at a distance x from the centre in the situations (a) and (b).

Video Solution

Text Solution

Verified by Experts

Given : A sphere is uncharged metallic
sphere . Due to inductin the charge
induced at the inner surface = - q and that
in outer surface =+q
(a) Hence the surface charge density at
inner and outer surface.
= charge/ total surface area
$= - \frac{q}{4} π (a^{2}) and \frac{q}{4} π (a^{2}) r e s p e c t i v e l y$
$(b) A g a \in if a \neg h e r c h a r \geq Q i s a d d e d \to < b r > t h e s u r f a c e, < b r > W e h a v e \in \neq r s u r f a c e c h a r \geq d e n s i t y < b r >$ = - q/ 4 pi (a^2).
Because the added charge does not affect
it on the other hand the external surface
charge density = $(q + \frac{Q}{4} m^{2})$ as the Q gets
added up
(c) For electric field let us assume in
imaginary surface area inside the surface
at a distance x from centre this is same in
both the cases as the q is ineffective.
$N o w, E . d s = \frac{q}{ε_{0}}$
$S o, E = \frac{q}{ε_{0}} \times \frac{1}{4} π x^{2} = (\frac{Q}{4} π ε_{0} (x^{2}))$ .

Updated on:21/07/2023

If charge q induced on outer surface of sphere of radius R, then intensity at point P at distance S from centre is
Ainversely proportional to ${(S + R)}^{2}$
Binversely proportional to $R^{2}$ .
Cinversely proportional to $S^{2}$ .
Ddirectly proportional to $S^{2}$ .
A charge 'Q' is placed at the centre of a hemispherical surface of radius 'R'. The flux of electric field due to charge 'Q' through the surface of hemisphere is
A $Q / 4 ε_{0}$
B $Q / 4 π ε_{0}$
C $Q / 2 ε_{0}$
D $Q / 2 π ε_{0}$