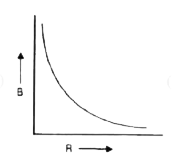
A charge Q is uniformaly distributed over the surface of non-conducting disc of radius R . The disc rotates about an axis perpendicular to its plane and passing through its centre with an angular velocity ω , As a result of this rotation a magnetic field of induction B is obrained at the centre of the disc . If we keep both the amount of charge placed on the disc and its angular velocity to be constant and vary the radius of the disc then the variation fo the magnetic induction at the centre of the disc will be represented by the figure :
The correct Answer is:B
dB=μ0(dQ)2r(ω2π)
∴b=∫dB=μ0ω4π⋅QπR22π∫20rdrr
=μ0ωQ2πR2×R
B=μ0ωQ2πR
B∝1R
Topper's Solved these Questions
- 15 MAGNETIC EFFECTS OF CURRENTSBOOK - MODERN PUBLICATIONCHAPTER - 15 MAGNETIC EFFECTS OF CURRENTSEXERCISE - Recent Competitive Questions
31 Videos
- 15 MAGNETIC EFFECTS OF CURRENTSBOOK - MODERN PUBLICATIONCHAPTER - 15 MAGNETIC EFFECTS OF CURRENTSEXERCISE - Multiple choice questions (Level - II) Paragraph questions
42 Videos
- ATOMS, MOLECULES AND NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - ATOMS, MOLECULES AND NUCLEIEXERCISE - Recent Competitive Questions
40 Videos
Similar Questions
A charge Q is uniformly distributed over the surface of non - conducting disc of radius R. The disc rotates about an axis perpendicular to its plane and passing through its centre with an angular to its plane and passing through its centre of the disc. If we keep both the amount of charge placed on the disc and its angular velocity to be constant and vary the radius of the disc then the variation of the magnetic induction at the centre of the disc will br represented by the figure:
View SolutionA charge q is uniformly distributed on a non-conducting disc of radius R. It is rotated with an angular speed co about an axis passing through the centre of mass of the disc and perpendicular to its plane. Find the magnetic moment of the disc.
View Solution
Knowledge Check
A charge Q is uniformly distributed over the surface of non - conducting disc of radius R. The disc rotates about an axis perpendicular to its plane and passing through its centre with an angular to its plane and passing through its centre of the disc. If we keep both the amount of charge placed on the disc and its angular velocity to be constant and vary the radius of the disc then the variation of the magnetic induction at the centre of the disc will br represented by the figure:
A B
B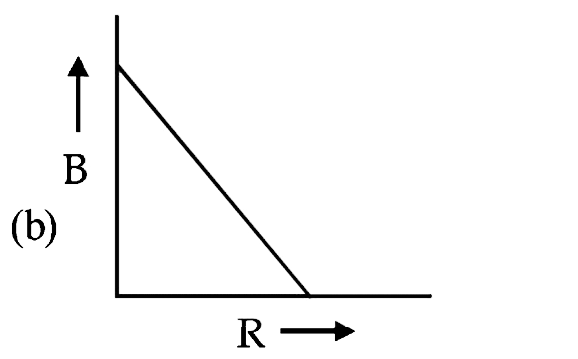 C
C D
D
Radius of gyration of disc rotating about an axis perpendicular to its plane passing through through its centre is (If R is the radius of disc)
AR2BR√2CR√3DR3A non conducting disc of radius R, charge q is rotating about an axis passing through its centre and perpendicular to its plane with an angular velocity ω charge q is uniformly distributed over its surface. The magnetic moment of the disc is
A14qωR2B12qωRCqωRD12qωR2
A charge q is uniformly distributed on a non-conducting disc of radius R. It is rotated with an angular speed co about an axis passing through the centre of mass of the disc and perpendicular to its plane. Find the magnetic moment of the disc.
View SolutionCharge Q is uniformly distributed over a nonconducting ring of radius R and mass m. It is made to rotate about an axis passing through its centre and perpendicular to its plone with an angular velocity of rotation ω. Find its magnetic dipole moment and its ratio with angular momentum.
View SolutionA non-conducting thin disc of radius R charged uniformly over one side with surface density σ, rotates about its axis with an angular velocity ω. Find (a) the magnetic field induction at the centre of the disc (b) the magnetic moment of the disc.
View SolutionA flat dielectric disc of radius R carries an exces charge on its surface. The surface charge density σ. The disc rotastes about an axis perpendicular to its lane passing thrugh the centre with angulasr velocity ω. Find the toruque on the disc if it is placed in a uniform magnetic field B directed perpendicular to the rotation axis.
View SolutionA flat dielectric disc of radius R carries an exces charge on its surface. The surface charge density σ. The disc rotastes about an axis perpendicular to its lane passing thrugh the centre with angulasr velocity ω. Find the toruque on the disc if it is placed in a uniform magnetic field B directed perpendicular to the rotation axis.
View Solution
