A charged particle with specfic charge q/m starts moving in the region of space where there are unifrom mutually perpendicular electric and magnitude fields. The magentic field is constant and has an induction B while the strength of the electric field varies with time as E=Emcosωt, where ω=qB/m. For the non-relativistic case find the law of motion x(t) and y(t) of the particle if at the moment t=0 it was located at the point O (see Fig). What is the appoximate shape of the trajectory of the particle?
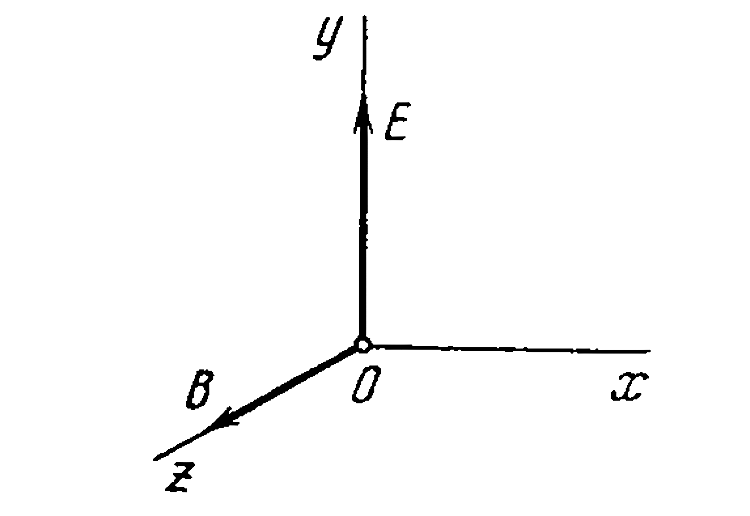
The equactions are as in 3.392.
dvxdt=qBmvy,dvydt=qEmmcosωt−qBmvx and dvxdt
with ω=qBm,ξ=vx+ivy, we get,
dξdt=IEmBωcosωt−iωξ
or mutiplying by eiωt
ddt(ξ,eiωt)=iEm2Bω(eiωt+1)
on intergrating, ξeiωt+Em4Beiωt+Em2Biωt
or, ξ=Em4B(eiωt+2iωteiωt)+Ceiωt
since ξ=0 at t=0,C=−Em4B,
Thus, ξ=iEm2Bsinωt+iEm2Bωteiωt
or, vx=Em2Bωtsinωt and vy=Em2Bsinωt+Em2Bωtcosωt
Intergrating again,
x=a2ω2(sinωt−ωtcosωt),y=a2ωtsinωt.
where, a=qEmm, and we have used x=y=0, at t=0
The trajectory is an unwinding spiral.
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electromagnetic Induction
84 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
A particle with specific charge q/m moves in the region of space where there are unifrom mutually perpendicular electric and magnetic fields with strength E and induction B (fig). At the moment t=0 the particle was located at the point O and had zero velocity. For the non-relativistic case find:
(a) the law of motion x(f) and y(t) of the particle, the shape of the trajectory,
(b) the lenght of the segment of the trajectory between two nearest points at which the velocity of the particle turns into zero,
(c) the mean value of the particle's velocity vector projections on the x axis (the drift velocity).
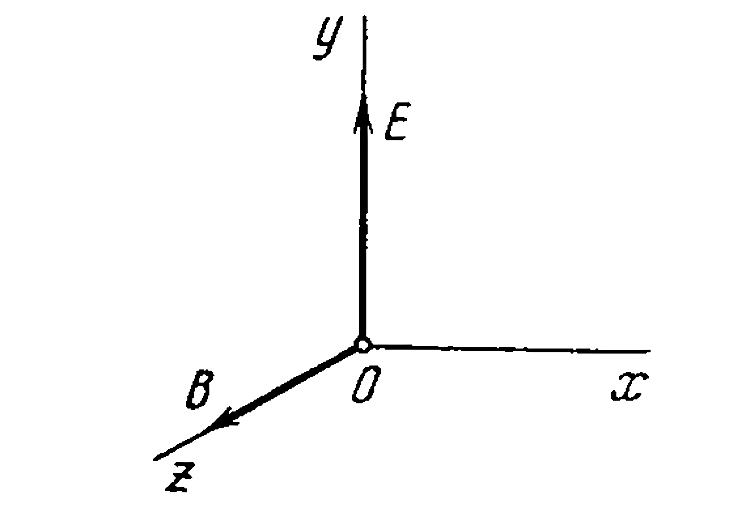
View SolutionA charged particle of specific charge s moves undeflected through a region of space containing mutually perpendicular and uniform electric and magnetic fields, E and B. When the field E is switched off, the particle will move in a circular path of radius
View Solution
Knowledge Check
A charged particle of specific charge s moves undeflected through a region of space containing mutually perpendicular and uniform electric and magnetic fields, E and B. When the field E is switched off, the particle will move in a circular path of radius
AEBsBEsBCEsB2DEB2sMutually perpendicular electric and magnetic fields are given by E = 1500 V/m and B = 0.04 T . Then velocity is given by
A60 m/sB3.75×106 m/sC3.75×104 m/sD60×104 m/sIn a certain region of space the electric potential V is known to be constant. Is the electric field in this region (a) positive (b) zero ,or (c ) negative ?
AAlso constantBPositiveCNegativeDZero
A charged particle of specific charge s moves undeflected through a region of space containing mutually perpendicular and uniform electric and magnetic fields, E and B. When the field E is switched off, the particle will move in a circular path of radius
View SolutionA beam of non-relativistic charged particles moves without deviation through the region of space A where there are transverse mutually perpendicular electric and magnetic fields with strength E and induction B. When the magnetic field is switched off, the trace of the beam on the screen S shifts by Δx. Knowing the distance a and b, find the specific charge q/m of the particles.
View SolutionA beam of non-relatitivistic chagred particles moves without deviation through the region of space A (fig) where there are transerve mutually perpendicular electric and magnetic fields with streght E and induction B. When the magnetic field is swichted off, the trace of the beam on the screen S shifts by Δπ. Knowing the distances a and b, find the spefic charge q/m of the particles.

View SolutionNon-relativistic protons move rectinearly in the region of space where there are unifrom mutually perpendicular electric and magnetic fields with E=4.0kV/m and B=50mT. The trajectory of the protons lies in the plates xz (Fig) and forms an angle φ=30∘ with the x axis. Find teh pithc of the helical trajectory along which the protons will move after the electric field is swiched off.
View SolutionAn oil drop having a charge q and apparent weight W falls with a terminal speed v in absence of electric field . When electric field is switched on it starts moving up with terminal speed v. The strength of electric field is
View Solution
