A circular brass loop of radius a and resistance R is placed with it plane perpendicular to a magnetic field, which varies with time as B=B0sinωt. Obtain the expression for the induced current in the loop.
Induced current,
I=Inducede.m.f.resistanceeR
=−dϕ/dtR=−1Rddt(BAcos0∘)
I=−ARddt(B0sinωt)=−AB0Rcosωt(ω)
=−AωB0R
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Solved Examples (b)1videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Short Answer Qusetions2videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise191videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - II Focus multiple choice question5videos
ELECTROMAGNETIC WAVES
Similar Questions
A conducting metal circular-wire-loop of radius r is placed perpendicular to a magnetic field which varies with time as B=B0e−t/τ, where B0andτ are constants, at time = 0. If the resistance of the loop is R then the heat generated in the loop after a long time (t→∞) is :
View SolutionA conducting loop of area A is placed in a magnetic field which varies sinusoidally with time as B=B0sin
View Solution
Knowledge Check
- Question 1 - Select One
A circular wire loop of radius r lies in a uniform magnetic field B, with its plane perpendicular to magnetic field. If the loop is deformed to a square shape in the same plane in time t, the emf induced in the loop is
AπBr2t(1−π2)BπBr2t(1−π3)CπBr2t(1−π4)DπBr2t(1−π5) - Question 2 - Select One
A conducting circular loop of raidus and resistance R is kept on a horiozntel plane. A vertical time varing magnetic field B=2t is switched on at time t=0. Then
Apower generated in the coil at any time t is constantBflow of charge passed through any section between timeCtotal charge passed through any section between time (t=0to=2is(4πa2R).DAll of the above - Question 3 - Select One or More
A uniform circular loop of radius a and resistance R palced perpendicular to a uniform magnetic field B. One half of the loop is rotated about the diameter with angular velocity ω as shown in Fig. Then, the current in the loop is
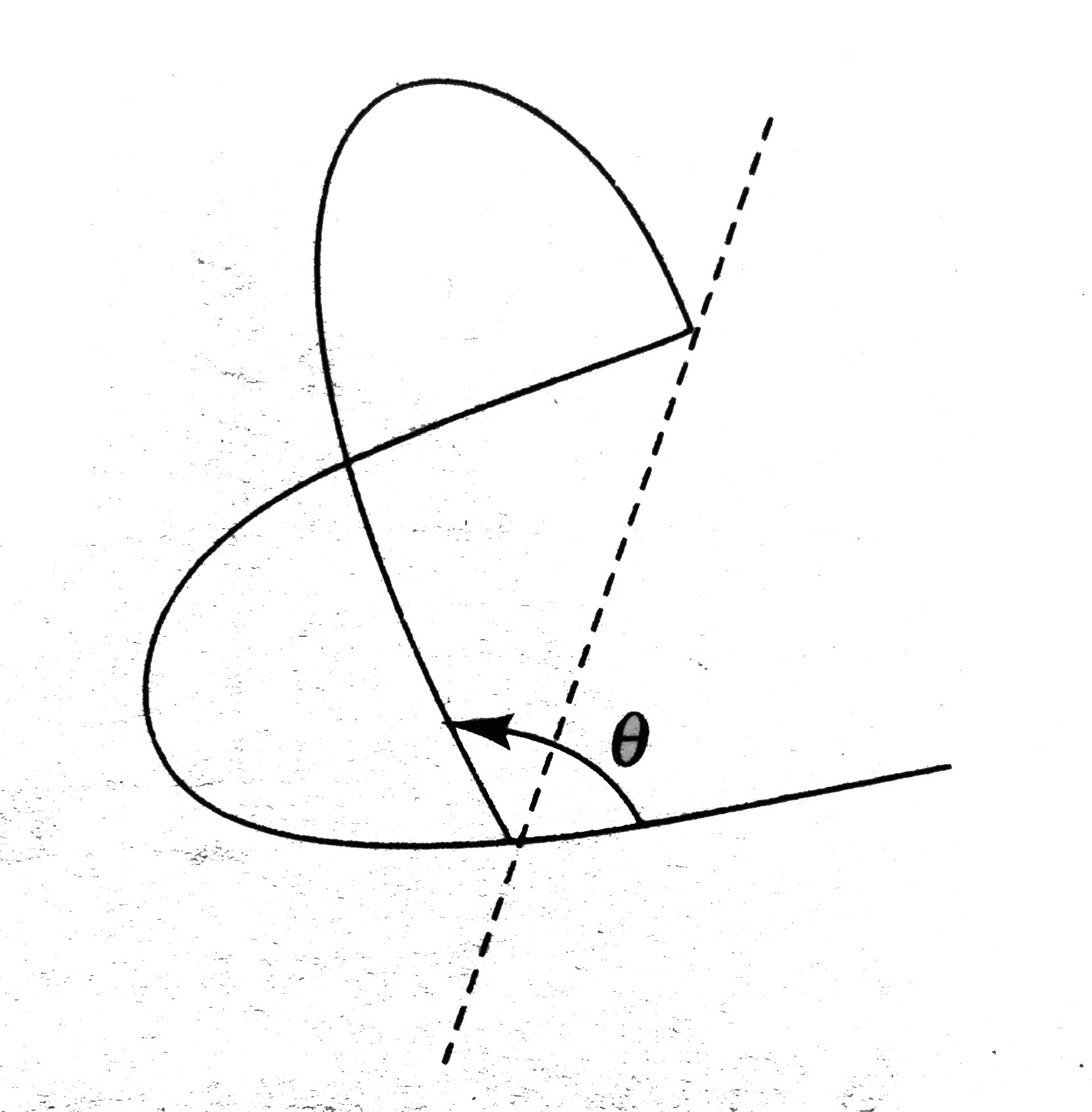 A(a) zero, when θ is zeroB(b) πa2Bω2R, when θ is zeroC( c) zero, when θ=π/2D(d) πa2Bω2R, when θ=π/2
A(a) zero, when θ is zeroB(b) πa2Bω2R, when θ is zeroC( c) zero, when θ=π/2D(d) πa2Bω2R, when θ=π/2
A conducting circular loop of face are 2.5X10−3m2 is placed perpendicular to a magnetic field which varies as B=(0.20T)sin[(50πs−1)t].(a)F∈dthechar≥jflow∈gthroughanycross−sectiondur∈gthetimet=0→t=40ms.(b)Iftheresistanceofthel∞pis10 Omega, find the thermal energy developed in the loop in this period.
View SolutionA plane loop shown in figure-5.71 is shaped in the from of two squares with sides a and b and it is introduced into a uniform magnetic field at right angles, to the loop's plane. The magnetic induction varies with time as B=B0sinωt. find the amplitude of the current induced in the loop if its resistance per unit length is equal to r. the induction of the loop is negligible.
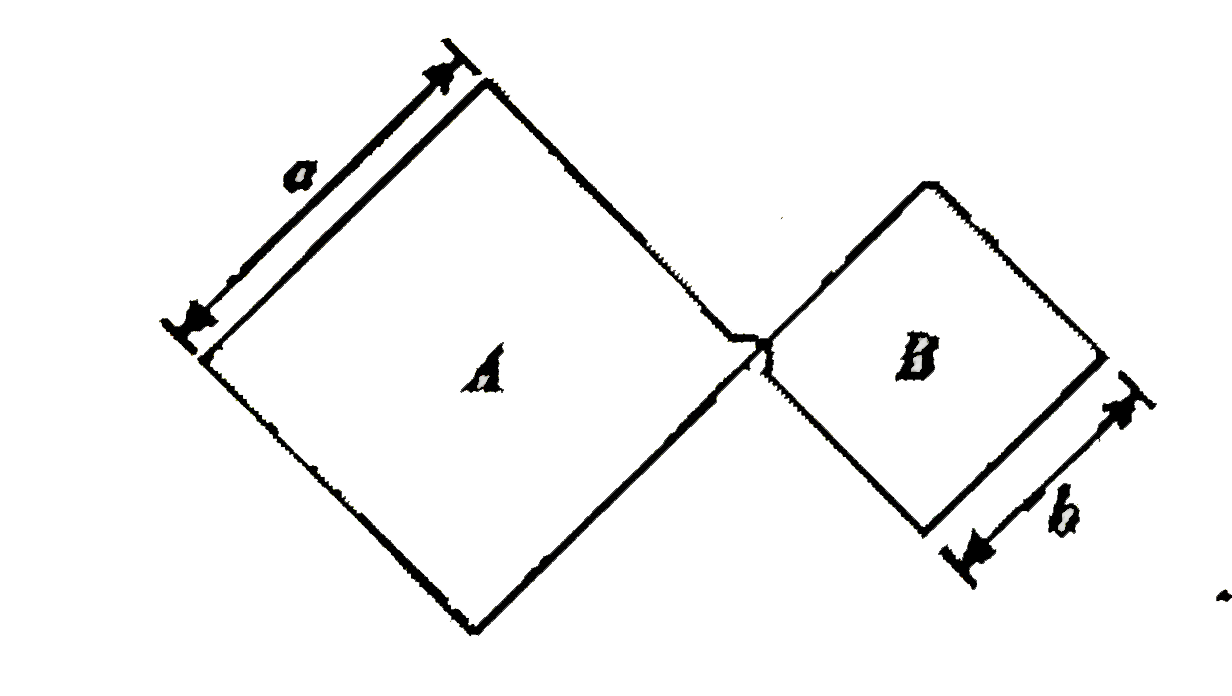 View Solution
View SolutionA circular conducting loop of area 100cm2 and resistance 3Ω is placed in a magnetic field with its plane perpendicular to the field. If the field is spatially uniform but varies with time t (in second) as B(t)=1.5cosωt tesla, the peak value of the current in the loop is
View SolutionA stationary circular loop of radius a is located in a magnetic field which varies with time from t=0→t=T according to law B=B0t(T−t). If plane of loop is normal to the direction of field and resistance of the loop is R, calculate
amount of heat generated in the loop during this interval.View SolutionA stationary circular loop of radius a is located in a magnetic field which varies with time from t = 0 to t = T according to law B=B0t(T−t). If plane of loop is normal to the direction of field and resistance of the loop is R, calculate
magnitude of charge flown through the loop from instant t = 0 to the instant when current reverses its direction.View Solution

