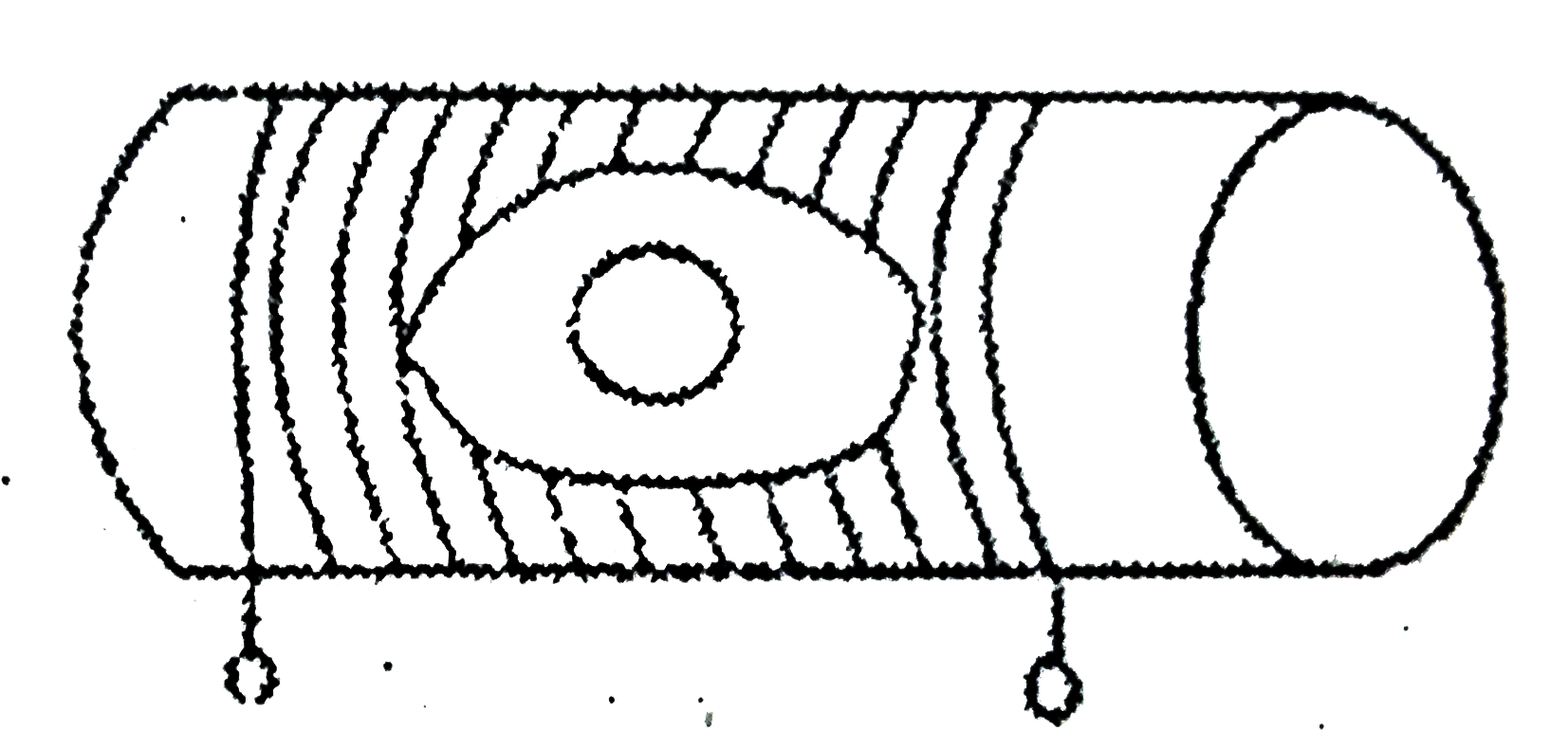
A circular coil with a cross-sectional area of $4 c m^{2}$ has 10 turns. It is placed at the center of a long solenoid that has 15 turns/cm and a cross sectional area of $10 c m^{2}$ , shown in the figure. The axis of the coil conicides with the axis of the solenoid. What is their mutual inductance?

A

$7.54 μ H$

B

$8.54 μ H$

C

$9.54 μ H$

D

$10.54 μ H$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Let us refer to the coil as circuit 1 and the soleniod circuite 2. The field in the central region of the solenoid is uniform, so the flux through the coil is
$ϕ_{12} = B_{A} A_{1} = (μ_{0} n_{2} I_{2}) A_{1}$
where $n_{2} = N_{2} / l = 1500$ turn/m
The mutual inductance si
$M = \frac{N_{2} ϕ_{12}}{I_{2}} = μ_{0} n_{2} N_{1} A_{1}$
$= (4 π \times 10^{- 7} T m A^{- 1}) (1500 m^{- 1}) (10) (4 \times 10^{- 4} m^{2})$
$7.54 \times 10^{- 6} H = 7.54 μ H$

|

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

The self inductance of a solenoid that has a cross-sectional area of $1 c m^{2}$ , a length of 10 cm and 1000 turns of wire is
A $0.86 m H$
B $1.06 m H$
C $1.26 m H$
D $1.46 m H$

NCERT FINGERTPS ENGLISH-ELECTROMAGNETIC INDUCTION-Inductance

Home
Ask Doubt
Profile