An ideal solenoid of cross-sectional area 10−4m2 has 500 turns per metre. At the centre of this solenoid, another coil of 100 turns is wrapped closely around it. If the current in the coil changes from 0 to 2 A in 3.14 ms, the emf developed in the second coil is
1 mv
2 mv
3 mv
4 mv
The correct Answer is:D
To solve the problem, we will use the concept of mutual inductance and the formula for induced electromotive force (emf) in the secondary coil due to a changing current in the primary coil.
1. Identify Given Values:
- Cross-sectional area of the solenoid, A=10−4m2
- Number of turns per meter of the solenoid, n1=500turns/m
- Number of turns in the secondary coil, n2=100turns
- Change in current, ΔI=2A−0A=2A
- Time interval, Δt=3.14ms=3.14×10−3s
2. Calculate the Rate of Change of Current:
dIdt=ΔIΔt=2A3.14×10−3s≈637.76A/s
3. Calculate the Mutual Inductance M:
The formula for mutual inductance M between the solenoid and the coil is given by:
M=μ0⋅n1⋅n2⋅A
where μ0=4π×10−7T⋅m/A (permeability of free space).
Substituting the values:
M=(4π×10−7)⋅(500)⋅(100)⋅(10−4)
Calculating this:
M=(4π×10−7⋅500⋅100⋅10−4)=4π×5×10−9=20π×10−9H
Approximating π≈3.14:
M≈20⋅3.14×10−9≈62.8×10−9H≈6.28×10−8H
4. Calculate the Induced EMF in the Secondary Coil:
The induced emf E in the secondary coil is given by:
E=−M⋅dIdt
Substituting the values:
E=−(6.28×10−8)⋅(637.76)
Calculating this:
E≈−(6.28×10−8⋅637.76)≈−4.0×10−5V
Since we are interested in the magnitude:
|E|≈4.0×10−5V=4.0mV
5. Final Answer:
The induced emf in the secondary coil is approximately 4mV.
- Cross-sectional area of the solenoid, A=10−4m2
- Number of turns per meter of the solenoid, n1=500turns/m
- Number of turns in the secondary coil, n2=100turns
- Change in current, ΔI=2A−0A=2A
- Time interval, Δt=3.14ms=3.14×10−3s
dIdt=ΔIΔt=2A3.14×10−3s≈637.76A/s
The formula for mutual inductance M between the solenoid and the coil is given by:
M=μ0⋅n1⋅n2⋅A
where μ0=4π×10−7T⋅m/A (permeability of free space).
M=(4π×10−7)⋅(500)⋅(100)⋅(10−4)
M=(4π×10−7⋅500⋅100⋅10−4)=4π×5×10−9=20π×10−9H
M≈20⋅3.14×10−9≈62.8×10−9H≈6.28×10−8H
The induced emf E in the secondary coil is given by:
E=−M⋅dIdt
Substituting the values:
E=−(6.28×10−8)⋅(637.76)
E≈−(6.28×10−8⋅637.76)≈−4.0×10−5V
|E|≈4.0×10−5V=4.0mV
The induced emf in the secondary coil is approximately 4mV.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION -C) Previous Years Questions
34 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION -D) Assertion-Reason type Question)
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION - A) (OBJECTIVE TYPE QUESTIONS)
35 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - comprehension
3 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
Similar Questions
For a toroid N = 500, radius = 40 cm, and area of cross section =10cm2. Find inductance
View SolutionA long solenoid of diameter 0.1m has 2×104 turns per metre. At the centre of the solenoid, a 100−turns coil of radius 0.01m is placed with its axis coinciding with the constant rate from +2A to 2A in 0.05s. Find the total charge (in μC) flowing through the coil during this time when the resistance of the coil is 40≠2Ω.
View Solution
Knowledge Check
A solenoid of cross-sectional area 2×10−4m2 and 900 turns has 0.6Am2 magnetic moment. Then the current flowing through it is
A2.4AB2.34mAC3.33AD3.33mAA long solenoid 'S' has 'n' turns per meter, with diameter 'a'. At the centre of this coil, we place a smallar coil of 'N' tunrs and diameter 'b' (where b lt a). If the current in the solenoid increase linearly with time, what is the induced emf apperaing in the smaller coil. Plot graph showing nature of variation in emf, if current varies as a function of mt2+C.
A B
B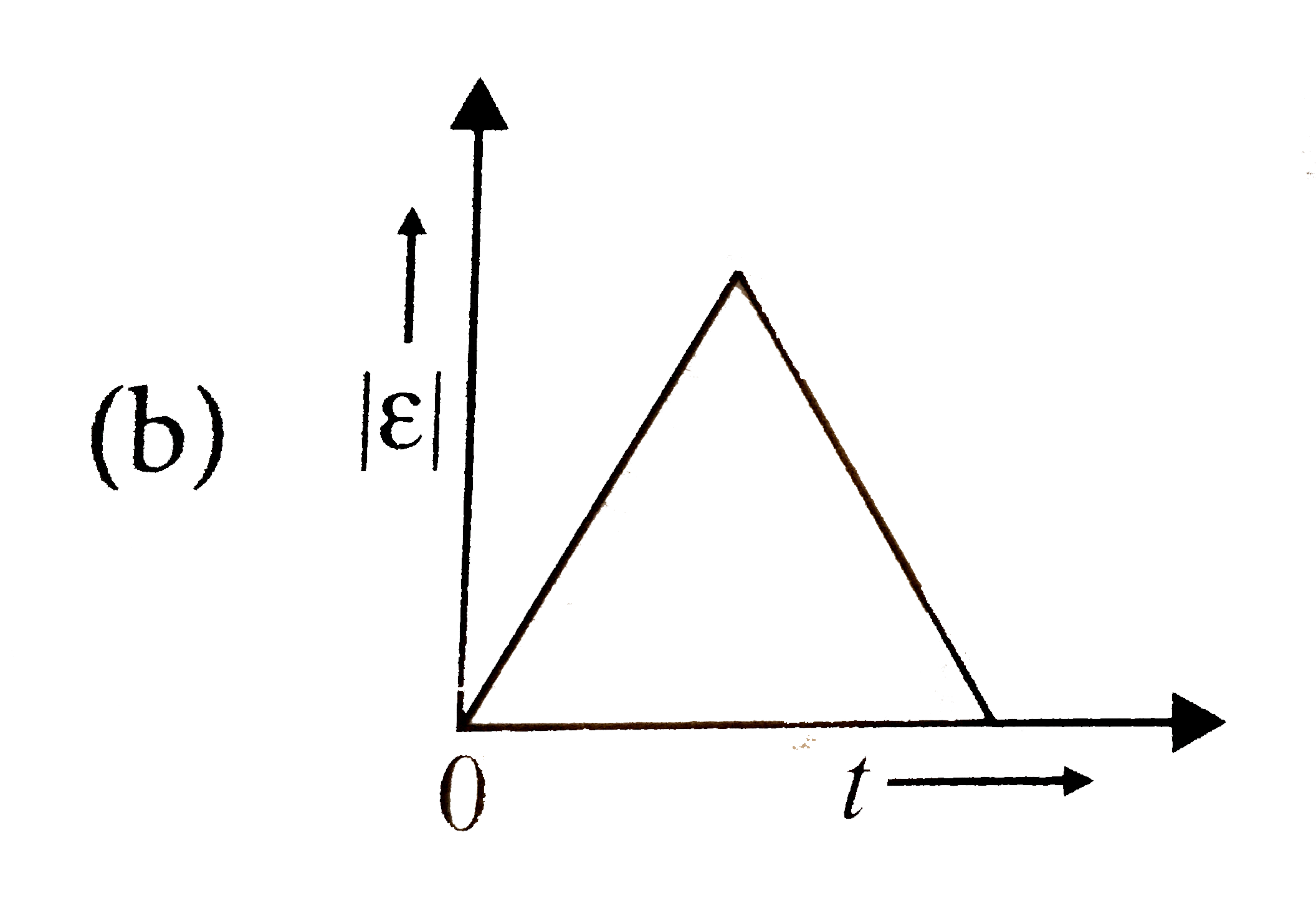 C
C D
D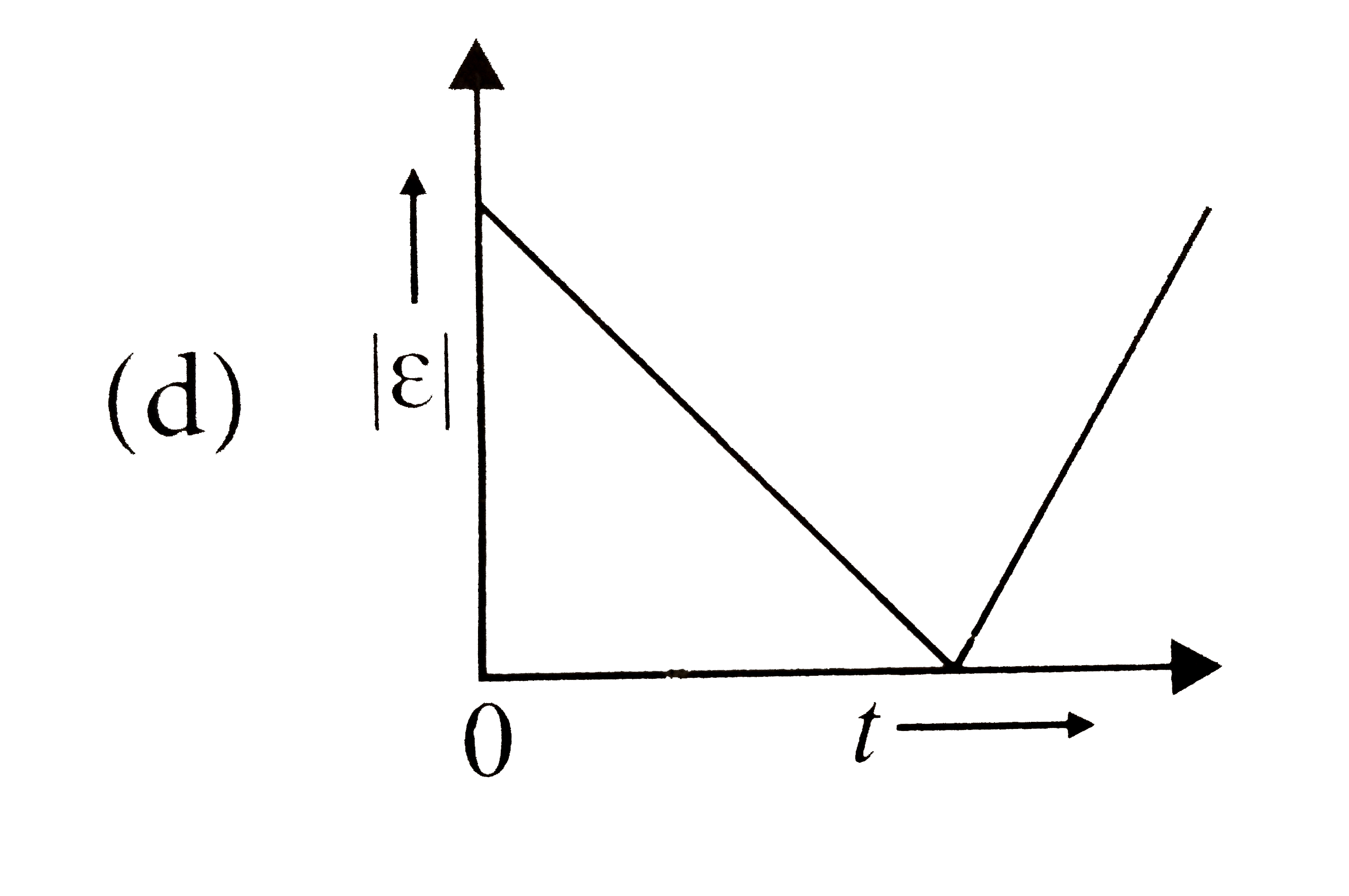
An air cored solenoid is of length 0.3 m, area of cross section 1.2×10−3m2 and has 2500 turns. Around its central section, a coil of 350 turns is wound. The solenoid and the coil are electrically insulated from eachother. Calculate the e.m.f. induced in the coil if the initial current of 3 A in the solenoid is reversed in 0.25 s.
View SolutionA long solenoid of cross-sectional area 5.0cm2 is wound with 25 turns of wire per centimetre. It is placed in the middle of a closely wrapped coil of 10 turns and radius 25 cm as shown.

(a) What is the emf induced in the coil when the current through the solenoid is decreasing at a rate −0.20A/s ?
(b) What is the electric field induced in the coil?
View SolutionA solenoid has a cross sectional area of 6.0×10−4m2, consists of 400 turns per meter, and carries a current of 0.40A.A10 turn coil is wrapped tightly around the circumference of the solenoid.The ends of the coil are connected to a 1.5Ω resistor.Suddenly, a switch is opened and the current in the solenoid dies to zero in a time 0.050s,Find the average current in the coil during the time.
View SolutionA circular coil with a cross-sectional area of 4cm2 has 10 turns. It is placed at the center of a long solenoid that has 15 turns/cm and a cross sectional area of 10cm2, shown in the figure. The axis of the coil conicides with the axis of the solenoid. What is their mutual inductance?
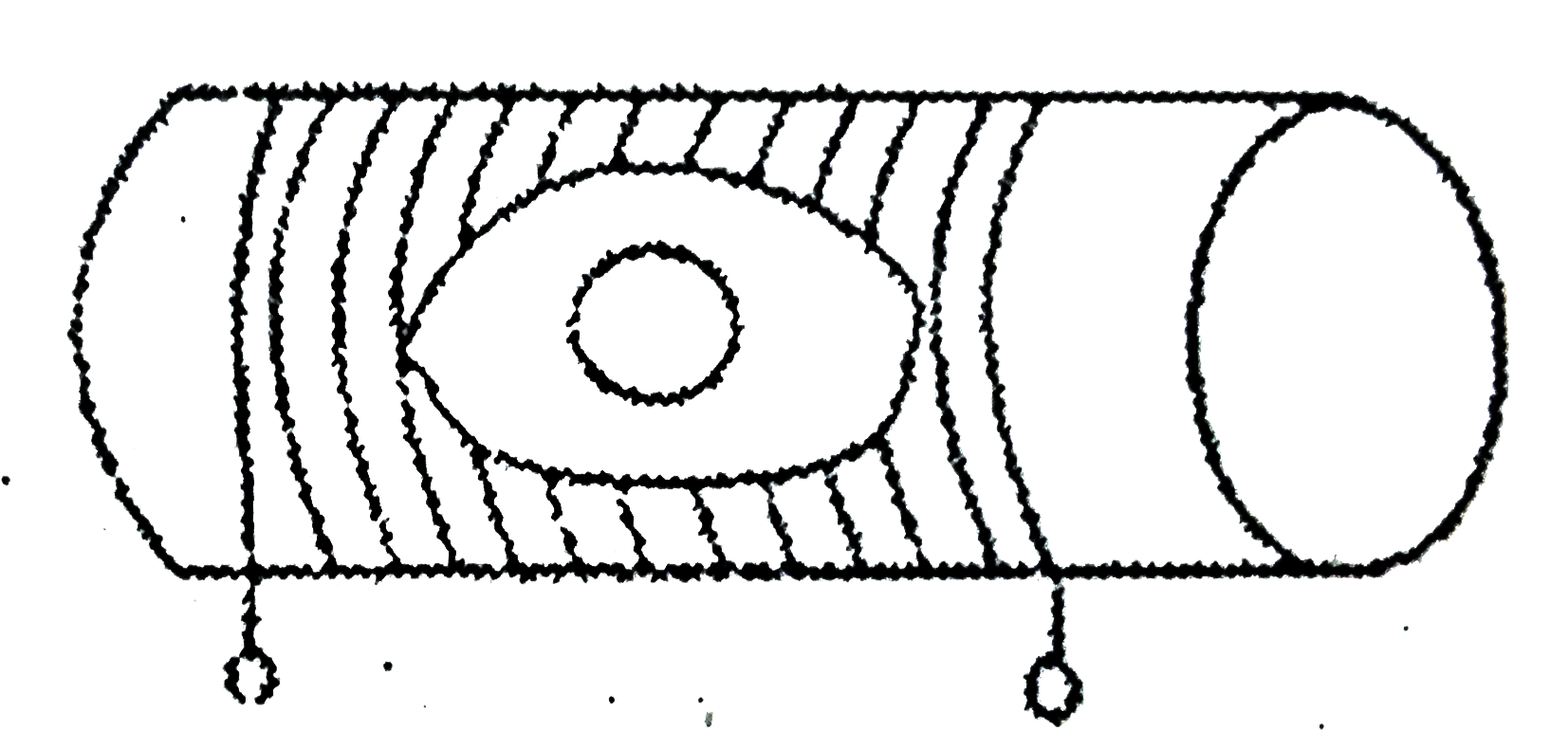
View SolutionA long solenoid of diameter 0.1 m has 2×104 turns per meter. At centre of the solenoid is 100 turns coil of radius 0.01 m placed with its axis coinciding with solenoid axis. The current in the solenoid reduce at a constant rate to 0A from 4 a in 0.05 s . If the resistance of the coil is 10π2Ω, the total charge flowing through the coil during this time is
View SolutionA long solenoid 'S' has 'n' turns per meter, with diameter 'a'. At the center of this coil, we place a smaller coil of 'N' turns and diameter 'b' (where b < a). If the current in the solenoid increase linearly with time, what is the induced emf appearing in the smaller coil. Plot graph showing nature of variation in emf, if current varies as a function of mt2+C.
View Solution