A circular copper ring of radius r translates in its plane with a constant velocity v. A uniform magnetic field b exists in the space in a direction perpendicular ot the plane of the ring. Consider different pairs of diametrically opposite points on the ring. (a) Between which pair of points is the emf? (b) Between which pair of points is the emf minimum? What is the value of this minimum emf?

Video Solution

Text Solution

Verified by Experts

(a) The emf is highest between the diameter perpendicular to the velocity because here length perpendicular to velocity is highest. $< b r >$ E_(max)-vB 2R $< b r >$ (b) The length perpendicular to velocity is lowest as the diameter is parallel to the velocity $< b r >$ E=_(min)=0.

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A ring of radius R is rolling on a horizontal plane with constant velocity v. There is a constant and uniform magnetic field B which is perpendicular to the plane of the ring. Emf across the lowest point A and right-most point C as shown in the figure will

AIncrease with time
Bdecrease with time
Cremains constant and equal to $\sqrt{2} B v R$
Dremains constant and equal to $B v R$
Question 2 - Select One

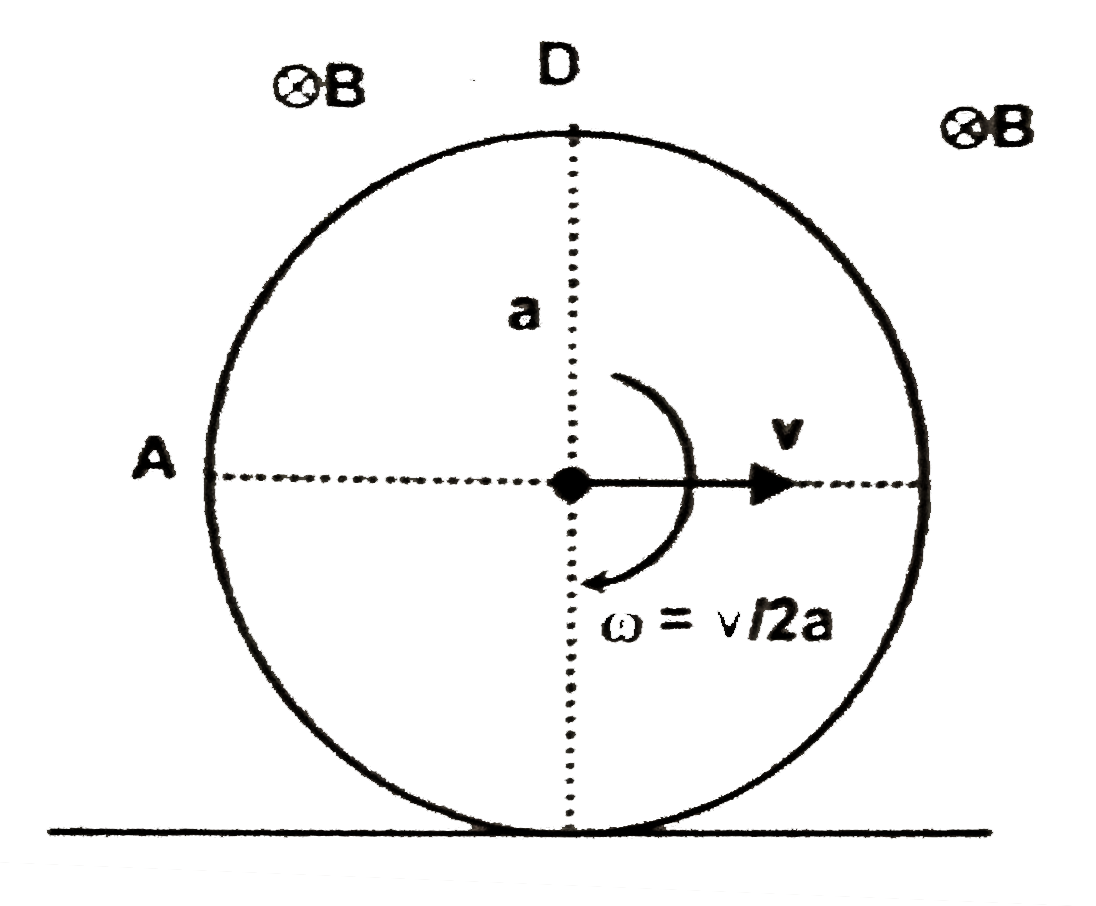
A circular conducting ring of radius 'a' is rolling with slipping on a horizontal surface as shown. A uniform magnetic field B is existing perpendicular to the plane of motion of the ring. The emf iniduced between the points A and D of the ring is
A $B ω a^{2}$
B $2 B ω a^{2}$
C $4 B ω a^{2}$
D $6 B ω a^{2}$
Question 3 - Select One or More
A conducting ring is placed in a uniform magnetic field with its plane perpendicular to the field . An $e m f$ is induced in the ring if
AIt is rotated about it axis
Bit is translated
Cit is rotated about a diameter
Dit is deformed

HC VERMA-ELECTROMAGNETIC INDUCTION-Exercises

Home
Ask Doubt
Profile