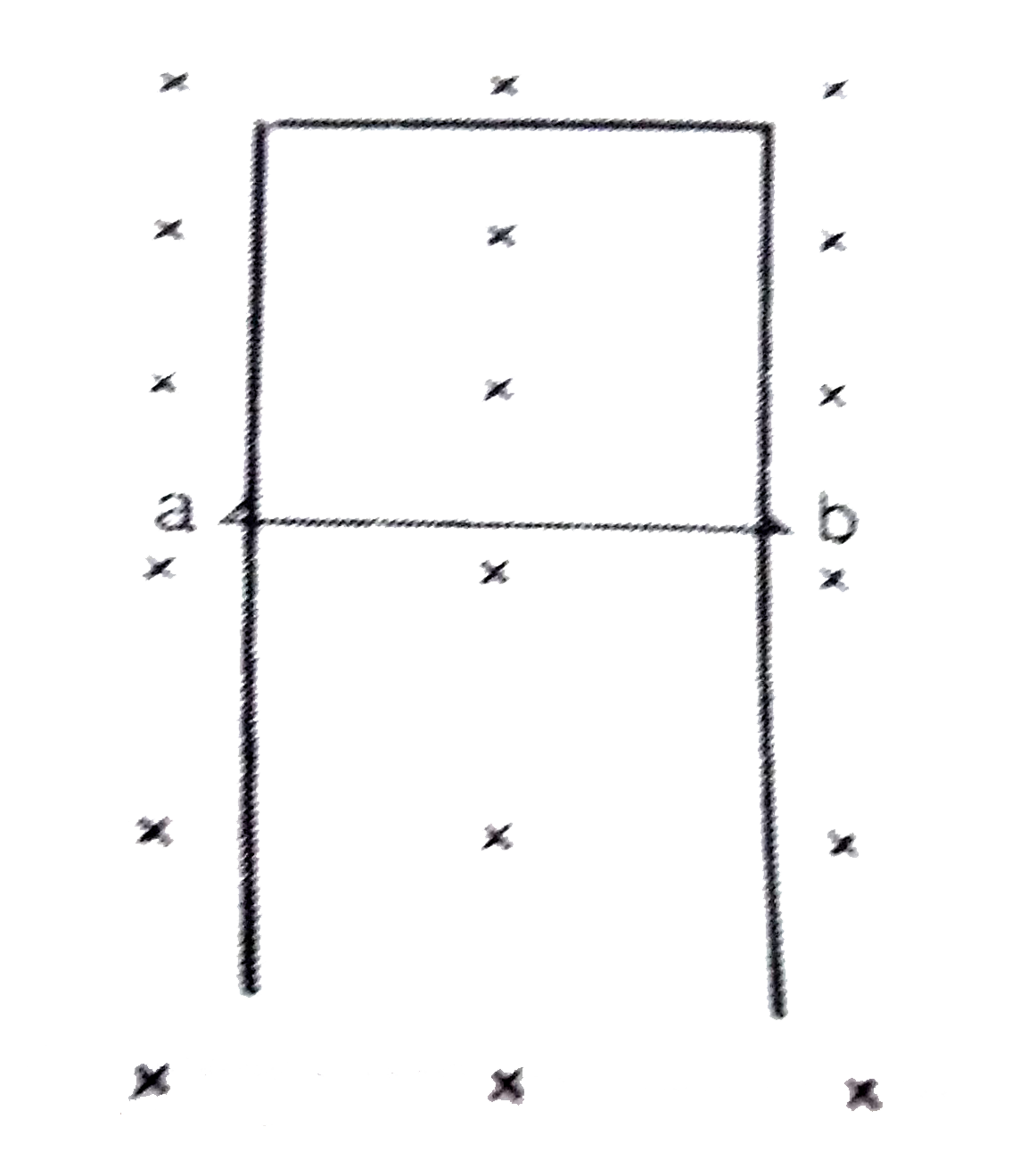
A conducting wire ab of length l, resistance r and mass m starts sliding at t = 0 down a smooth, vertical, thick pair of connected rails as shown in . A uniform magnetic field B exists in the space in a diraction perpendicular to the plane of the rails. (a) Write the induced emf in the loop at an instant t when the speed of the wire is v. (b) what would be the magnitude and direction of the induced current in the wire? (c) Find the downward acceleration of the wire at this instant. (d) After sufficient time, the wire starts moving with a constant velocity. Find this velocity v_m. (e) Find the velocity of the wire as a function of time. (f) Find the displacement of the wire as a functong of time. (g) Show that the rate of heat developed inte wire is equal to the rate at which the gravitational potential energy is decreased after steady state is reached.
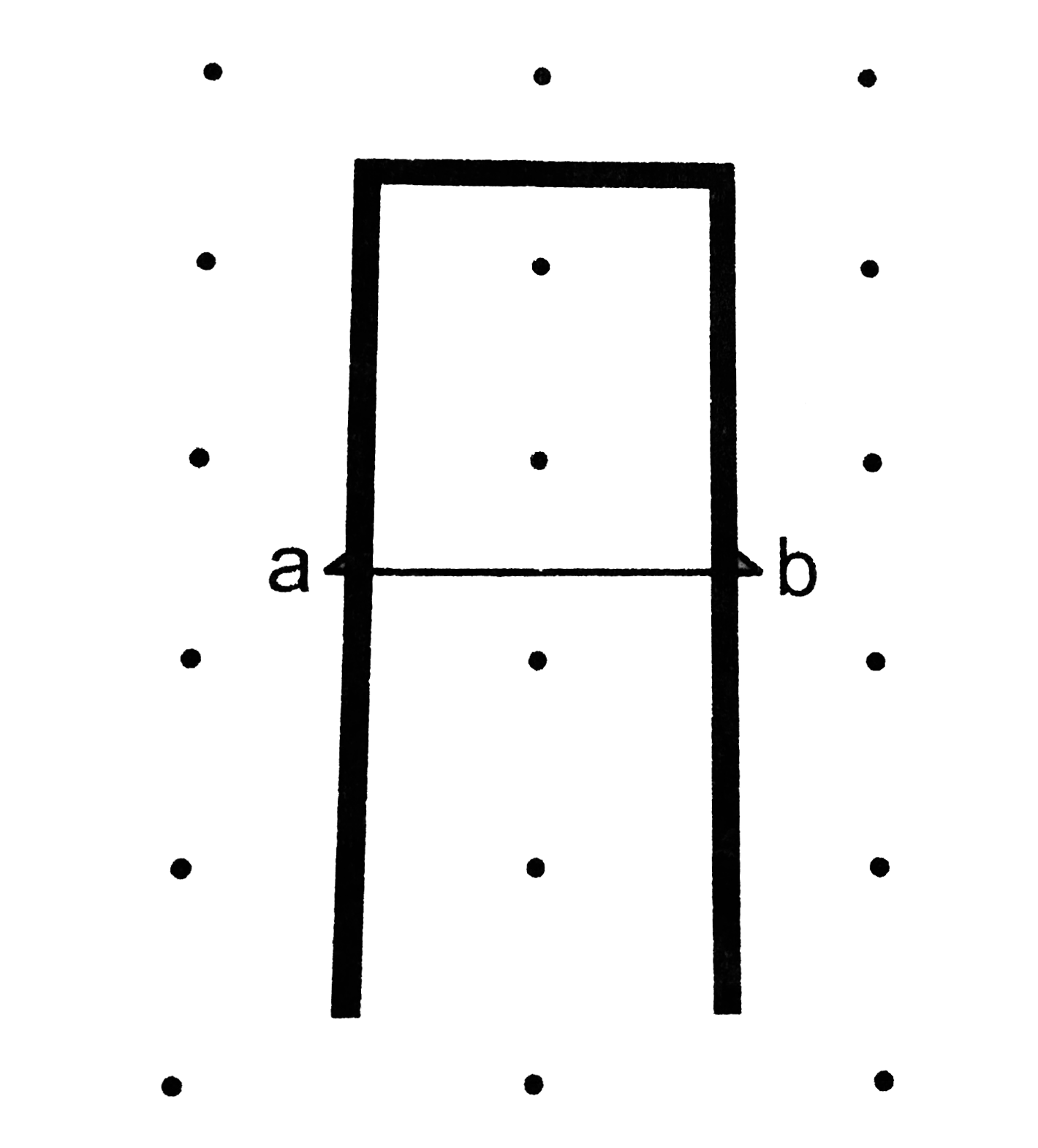
(a) when the speed the speed of wire is v
emf developed =Blv<br>(b) Induced current is the wire =(Blv)/R<br>(from b to a )<br>(c ) Downwards acceleration of the wire<br>=(mg-F)/m due to the current <br>=(ilB)/(m)=g=(B^2l^2v)/(Rm)<br>(d) let the start moving with constant velocity then acceleration =0<br>(B^2l^2v_m)/(Rm)=g<br> implies V_m=(GrM)/(B^2l^2)<br>(e) since (dv)/(dt)=a<br>implies (dv)/(dt)=((mg-B^2l^2v//R)/m) implies (dv)/((mg-B^2l^2v//R)/(m))=dt<br>int_(0)^(v)(m dv)/(mg-(B^2l^2v/R)/(m))=int_(0)^(v)dt<br>implies (m)/((B^2l^2v)/(R))[log (mg-((B^2l^2v)/(R))]_(0)^(v)=t<br> implies(-mR)/(B^2l^2)[log (mg-(B^2l^2v)/(R))-log(mg)]=t<br>⇒log⎡⎢⎣mg−B2l2vRmg⎤⎥⎦=−tB2l2mr
=log[1−B2l2vRmg]=−tB2l2mr
⇒1−(B2l2v)(Rmg)=e−tB2l2mr
⇒(1−e(−tB2l2))=B2l2vRmg
v−RmgB2l2(1−e(−tB2l2))
⇒v=vm(1−e−gtvm)[∴vm=RmgB2l2]
(f)sincedsdt=v
∫ds=∫v.dt
s=vm(1−e−gtvm)
=vm.(t+vmg.e−gtvm)
=(vmt+(vm)2ge−gtvm)−(Vm)2g
=vmt=(Vm)2g(1−e−gtvm)
(g) ddt(msg)=mg.dsdt
=mg.(vm)((1−e−gtvm)
dHdt=l2R=R.(lBvR)2
=l2B2v2R
=l2B2R.(Vm)2((1−e−gtvm)2
Aftersteadystatei.e..t→∞
ddt(msg)=mg(vm)ltbr>dHdt=l2B2R(vm)2
=(l^2B^2)/(r).(v_m).(mgR)/(l^2B^2)<br>Hence after steady state (d_H)/(dt)=(d)/(dt) mgs.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 2
10 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises
75 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercises
9 Videos
Similar Questions
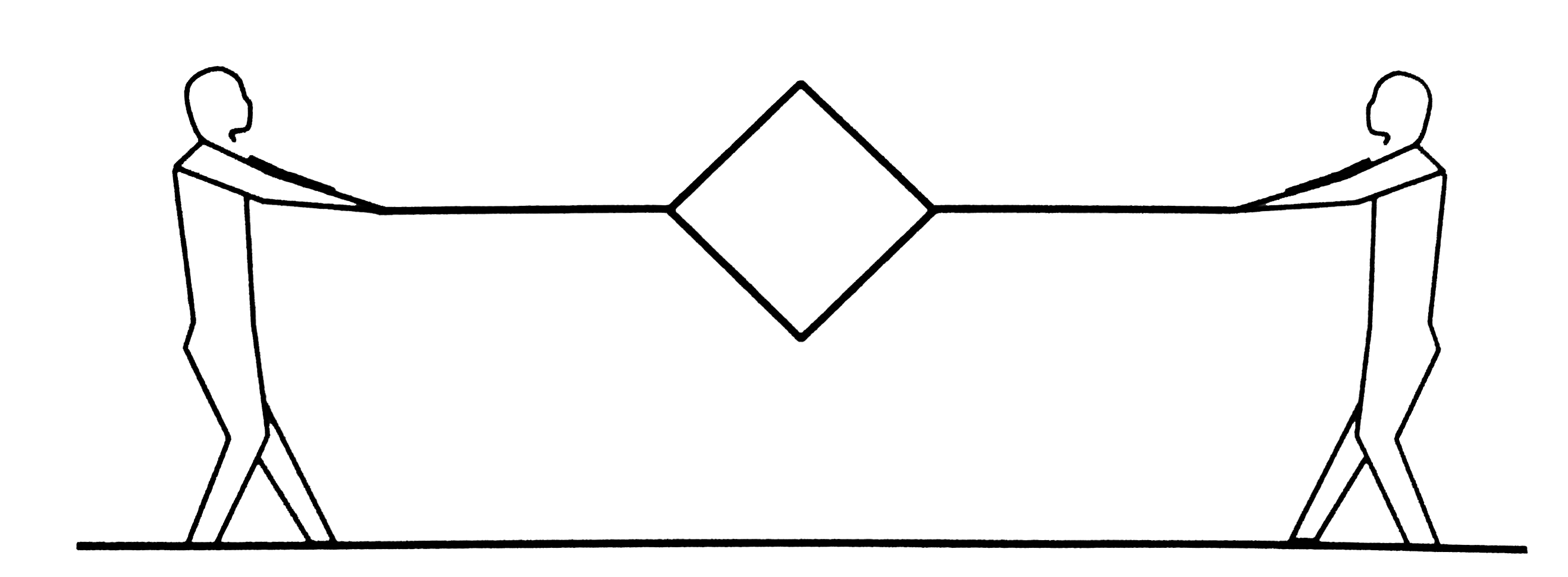
Shown a metallic square frame of edga a in a vertical plane. A uniform magnetic field B exists in the space in a directon perpendicular to the plane of the figure. Two boys pull the opposite corners of the square ot deform it into a rhombus. They start pulling the corners t t=0 and sisplace the corners at a uniform speed u. (a) find the induced emf in the frame at the instant when the angles at these corners reduce to 60∘. (b) find the induced current in the frame at this instatnt if the total resistance of the frame is R. (c) Find the total charge which flows through a side of the frame by the time the square is deformed into a straight line.
View SolutionA bar magnet is moved along the axis of a copper ring placed far away from the magnet. Looking from the side of the magnet, an anticlockwise current is found to be induced in the ring. Which of the following may be true?
View SolutionFind the dimensional formula of ε0 .
View SolutionShow that the dimensions of the displacement current (ω0dΦEdt) are that of an electric current.
View SolutionFigure shows a conducting rod of negligible resistance that can slide on smooth U-shaped rail made of wire of resistance 1Omega//m . Position of the conducting rod at t=0 is shown. A time dependent magnetic field B=2t tesla is switched on at t=0 The current in the loop at t=0 due to induced emf is
View SolutionA wire of length l , mass m and resistance R slides without any friction down the parallel conducting rails of negligible resistance . The rails are connected to each other at the bottom by a resistanceless rail parallel to the wire so that the wire and the rails form a closed rectangualr conducting loop. The plane of the rails makes an angle theta with the horizontal and a uniform vertical magnetic field of the inducetion B exists throughout the rregion. Find the steady state velocity of the wire.
View SolutionFigure showns a smooth pair of thick metallic rails connected across a battery of emfε having a negligible internal resistance.A wire ab of length l and resistance r can slide smoothly on the rails.The entire system lies in a horizontal plane and is immersed in a uniform vertical magnetic field B.At an instant t the wire at this instant. (b)What is the force acting on the wire at this instant. (c)Show that after some time the wire ab will slide with a constant velocity.Find this velocity.
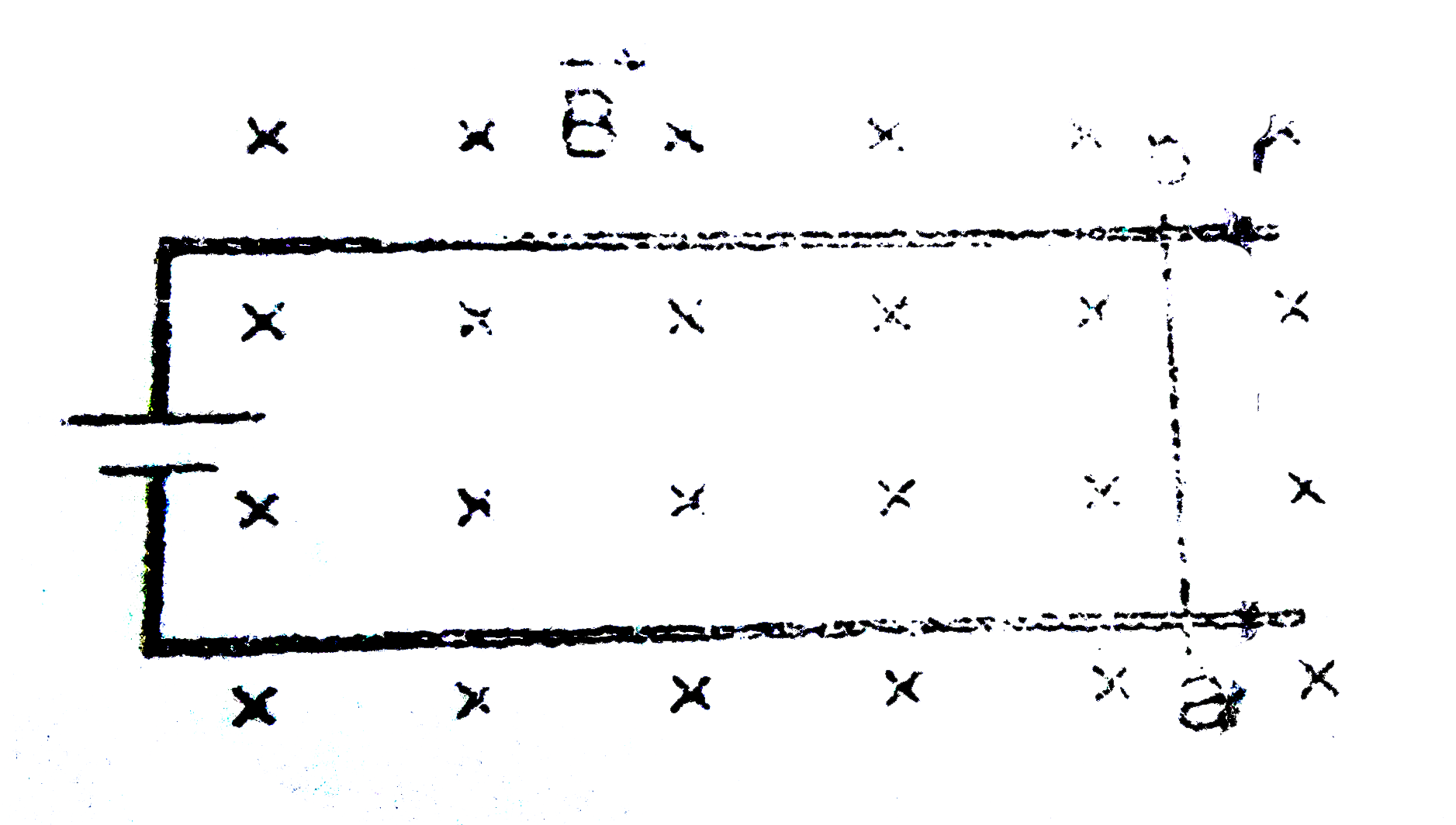
View SolutionA copper wire ab of length l, resistance r and mass m starts sliding at t=0 down a smooth, vertical, thick pair of connected condcuting rails as shown in figure.A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the rails which options are correct.
View SolutionA copper wire ab of length l, resistance r and mass m start sliding at t=0 down a smooth, vertical, thick pair of connected conducting rails as shown in figure. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the rails which options are correct .
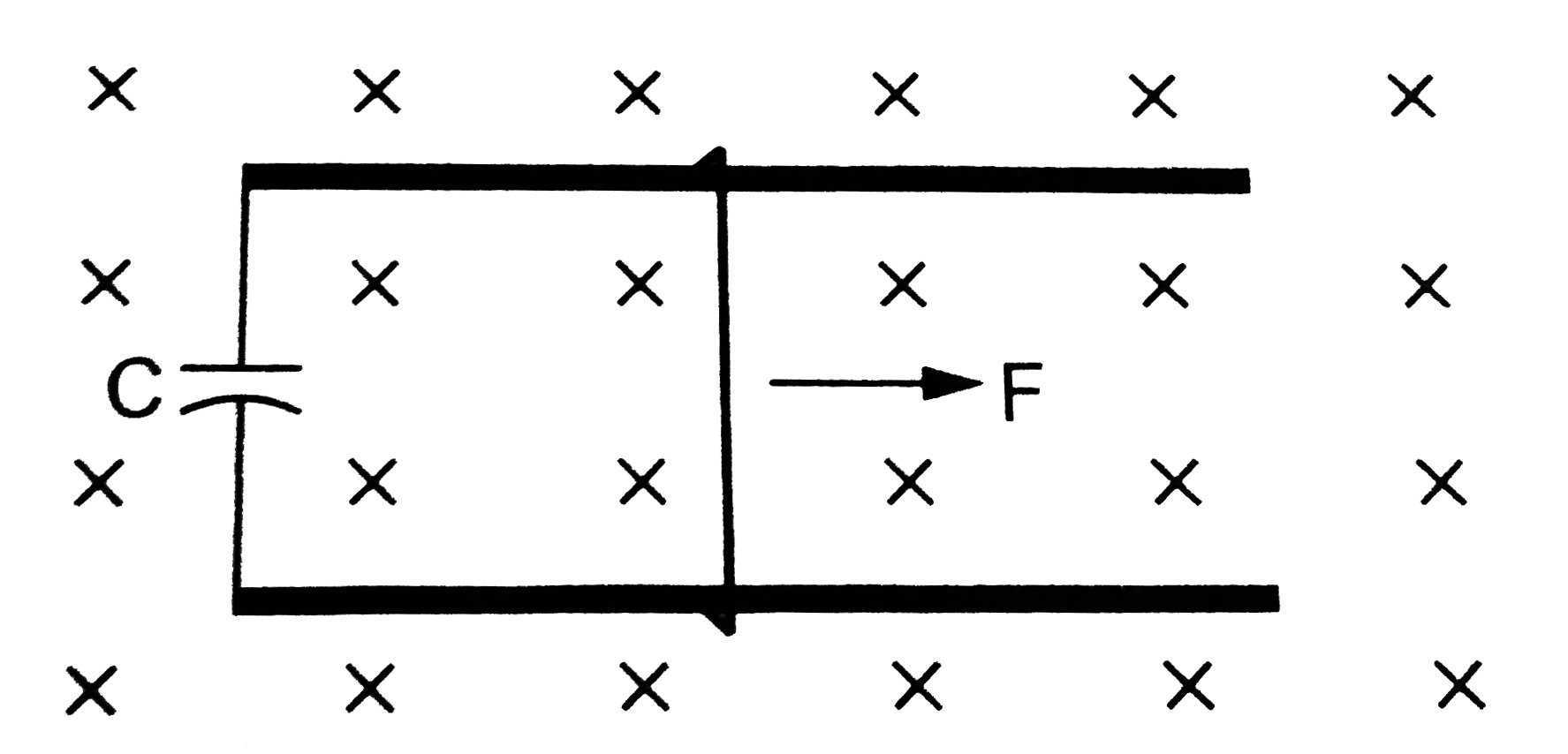
View SolutionA wire having mass m and length 1 can freely slide on a pair or parallel smooth horizontal rails placed in vertical magnetic field B. The rails are connected by a capacitor of capacitance C . The electric resistance of the rails and the wire is zero .If a constant force F acts on the Wire as shown in the figure . Then ,the acceleration of the wire can be given as

View SolutionA wire ab of length l, mass m and resistance R slides on a smooth thick pair of metallic rails joined at the bottom as shown in fig. The plane of the rails makes an angle theta with the horizontal. A vertical magnetic field B exist in the region. If the wire slides on the rails at a constant speed v, then the value of B is -
View SolutionA conducting wire ab of length l resistance r and mass m starts sliding down at t=0 on a smooth, vertical thick pair of connected rails as shown. The terminal speed of the wire is

View SolutionA wire of mass m and length I can freely slide on a pair of parallel, smooth, horizontal rails placed in a vertical magnetic field B . The rails are connected by a capacitor of capacitance C. The electric resistance of the rails and the wire is zero. If a constant force F acts on the wire as shown in the figure, find the acceleration of the wire.
View SolutionA wire ab of length l, mass m and resistance R slided on a smooth, thick pair of metallic rails joined at the bottom as shown in . The plane of the the rails makes an angle theta with the horizontal. A vertical magnetic field B exists in the ragion. if the wire slides on the rails at a constant speed v, show that B = sqrt(mg R sin theta)/(vl^2 cos^theta) .
View SolutionFigure shows a conducting rod of negligible resistance that can slide on smooth U-shaped rail made of wire of resistance 1Omega//m . Position of the conducting rod at t=0 is shown. A time dependent magnetic field B=2t tesla is switched on at t=0 The current in the loop at t=0 due to induced emf is
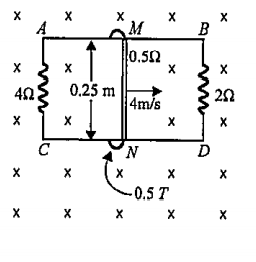
View SolutionA sliding wire of length 0.25 m and having a resistance of 0.5Ω moves along conducting guiding rails AB and CD with a uniform speed of 4m/s. A magnetic field of 0.5 T exists normal to the plane of ABCD directed into the page. The guides are short-circuited with resistances of 4 and 2Ω as shown. The current through the sliding wire is:
View Solution
