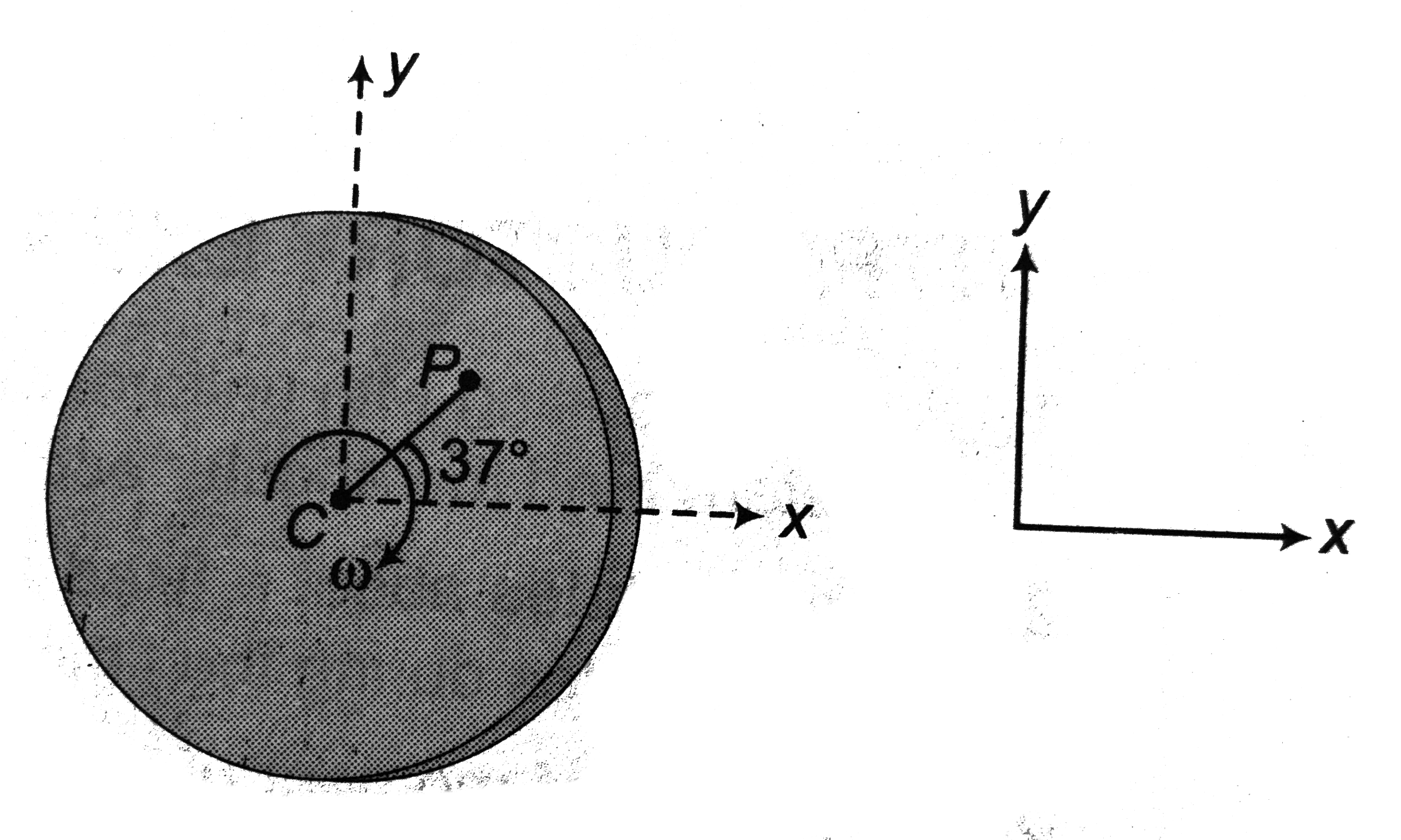
A circular disc is rotating with an angular speed (in radian per sec)
ω=2t2
given, CP=2m
In terms of ˆi,ˆj and ˆk at t=1s
find,
(a). ω
(b). α
(c). linear velocity of the particle lying at P (d). linear acceleration of the particle lying P
ω=2t2⇒α=dωdt=4t
at t=1s, ω=2rad/s and α=4rad/s2
for the particle at P, r=CP=2m
(a). Rotation is clockwise. So according to right hand rule ω is perpendicular to paper inwards along negative z-direction
∴ω=(−2ˆk)rad/s
(b). ω is increasing. so α is alos in the direction of ω
∴α=(−4ˆk)rad/s2
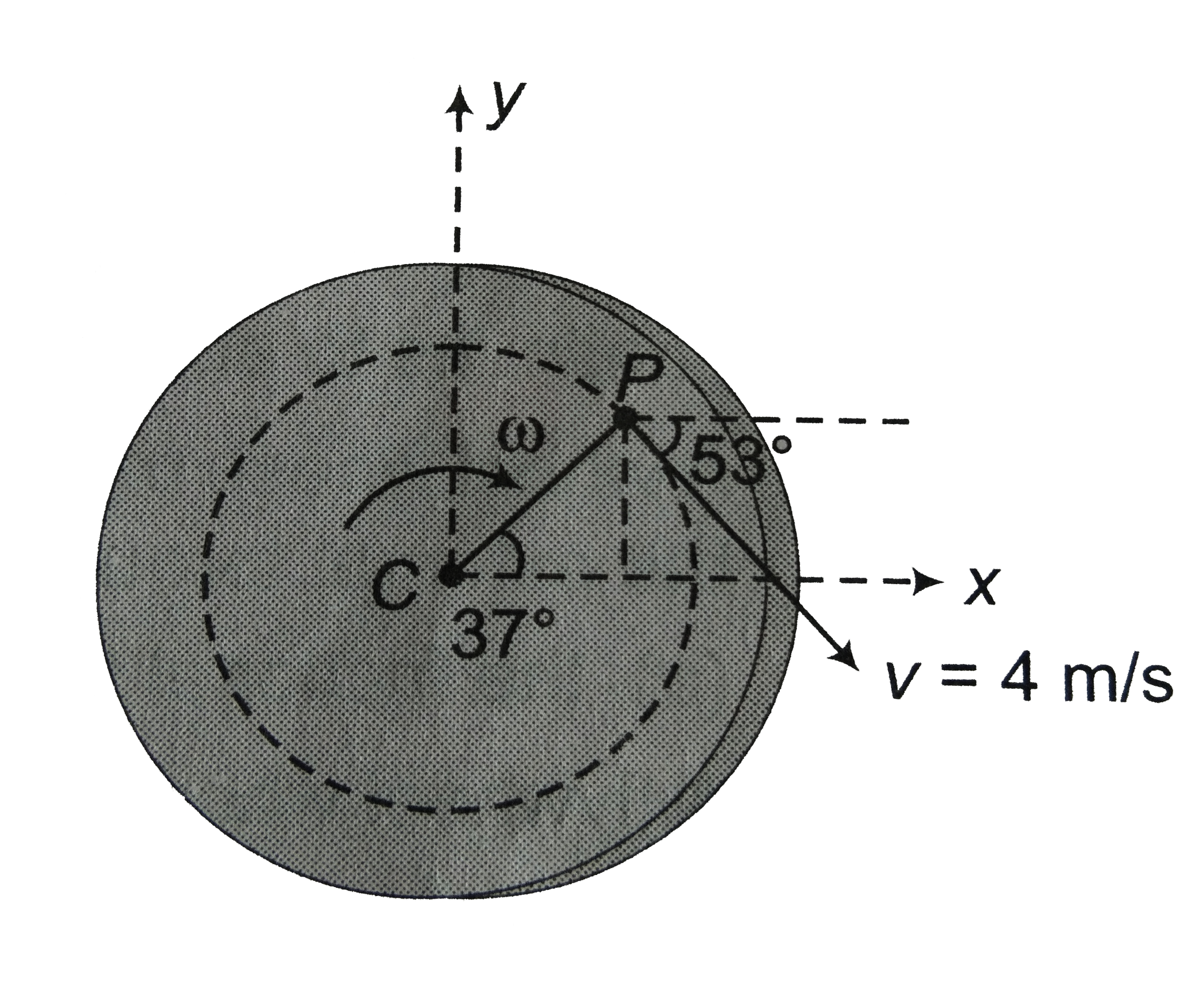
(c). v=rω=(2)(2)=4m/s
This velocity is tangential to the doted circle of P as shown in figure. ∴v=(4cos53∘)ˆi−(4sin53∘)ˆj
or v=(2.4ˆi−3.2ˆj)m/s
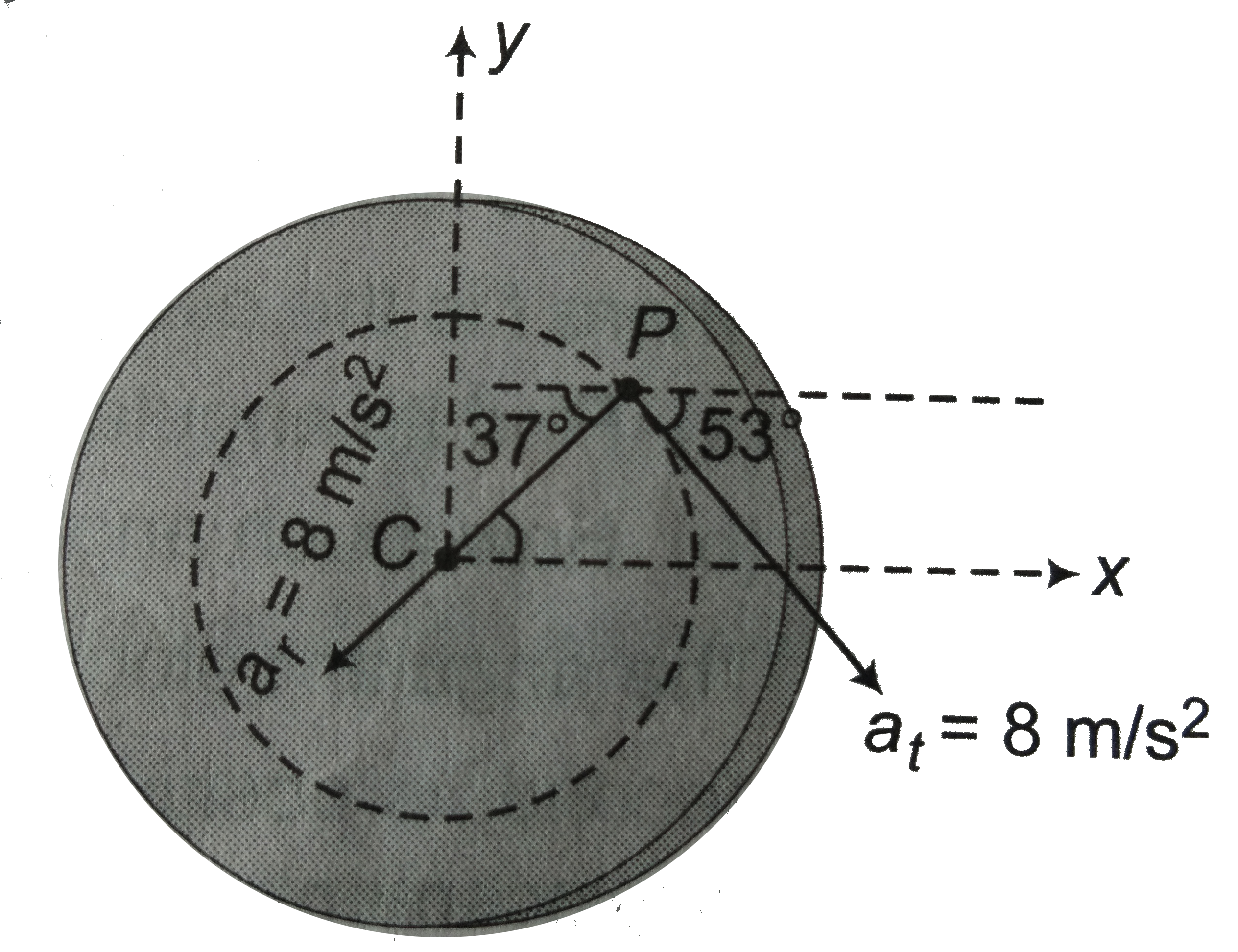
(d). Acceleration of the particle has two components
(i). ar=rω2 (radial component)
=(2)(2)2=8m/s2
this components is towareds centre C.
(ii). at=rα (tangential component)
=(2)(4)=8m/s2
this component is in the direction of linear velocity, as ω or v is increasing
∴a=(8cos53∘−8cos37∘)(ˆi)
+(8sin53∘+8sin37∘)(−ˆj)
or a=(−1.6ˆi−11.2ˆj)m/s2
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Examples25videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Miscellaneous Examples2videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions17videos
ROTATIONAL MOTION
Similar Questions
Velocity of a particle is given as v=(2t2−3)m/s. The acceleration of particle at t = 3s will be :
View Solution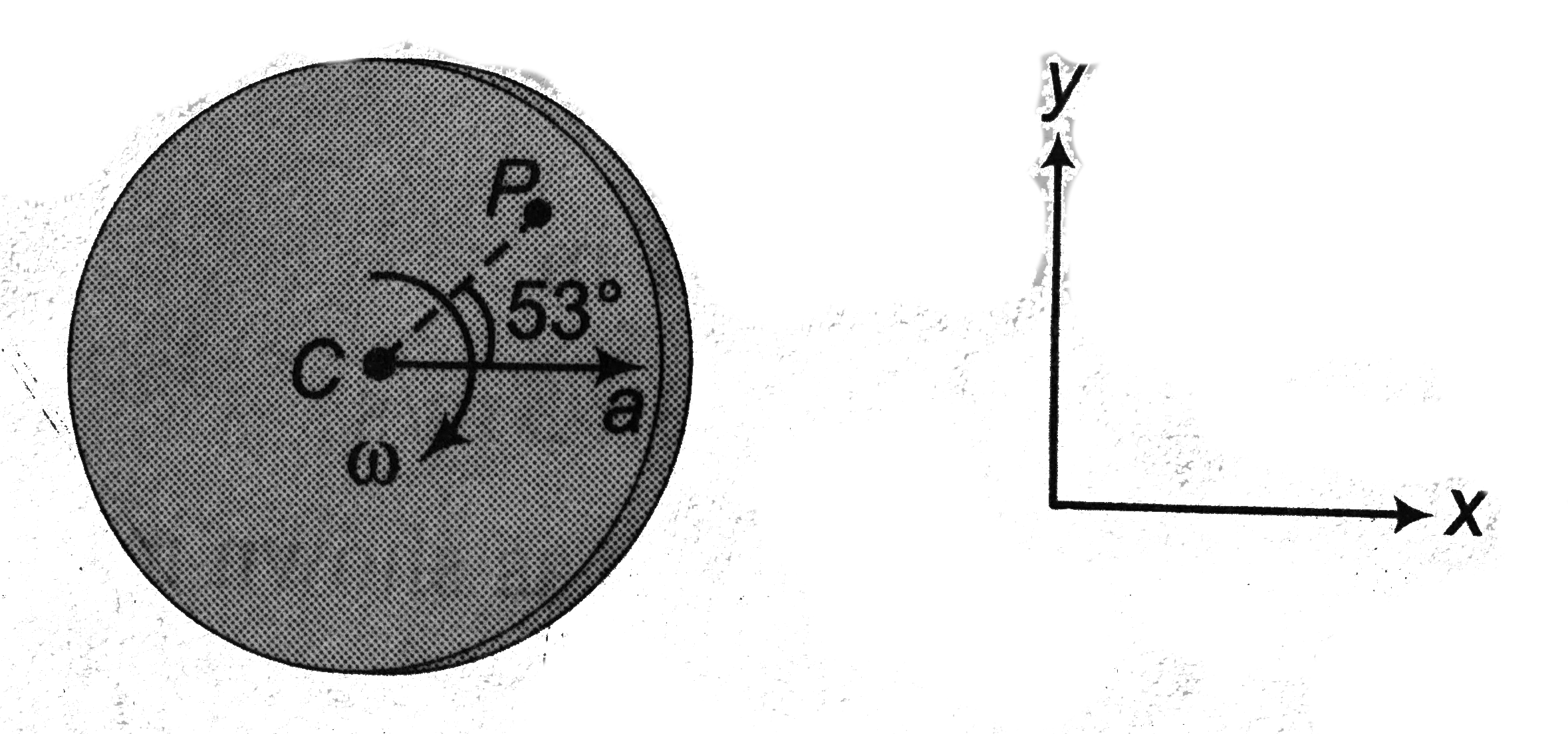
In the shown figure,
a=2m/s2,ω=(2t)rods−1 and CP=1m
In terms of ˆi and ˆj, find linear acceleration of the particle at P at P at t=1 sView Solutionthe angular velocity omega of a particle varies with time t as ω=5t2+25rads. the angular acceleration of the particle att=1s is
View SolutionA particle is revolving in a circle of radius 1 m with an angular speed of 12 rad/s. At t = 0, it was subjected to a constant angular acceleration α and its angular speed increased to (480π) rotation per minute (rpm) in 2 sec. Particle then continues to move with attained speed. Calculate
(i) angular acceleration of the particle,
(ii) tangential velocity of the particle as a function of time.
(iii) acceleration of the particle at t = 0.5 second and at t = 3 second
(iv) angular displacement at t = 3 second.View Solution
In the figure shown υ=2m/s ω=5rad/s and CP=1m
In terms of ˆi and ˆj find linear velocity of particle P.View SolutionA particle is moving along a circle of radius 20cm, with a linear velocity of 2m//s. Calculate the angular velocity of the particle.
View SolutionA particle is moving along a circle of radius 20cm, with a linear velocity of 2m//s. Calculate the angular velocity of the particle.
View SolutionIf a particle moves in a circle of radius of 4m at speed given by v=2t where v is in m/s and t in sec.At t=4s ,net accleration of particle will be:
View SolutionIf angular velocity of a particle having position vector →r=(2ˆi−2ˆj+2ˆk)m about the origin is →w=(2ˆi−2ˆj−ˆk)rads then magnitude of linear velocity of the particle will be
View SolutionThe angular velocity of circular disc of radius 2cm is 20 rad s−1. Calculate the linear velocity of the disc.
View Solution
