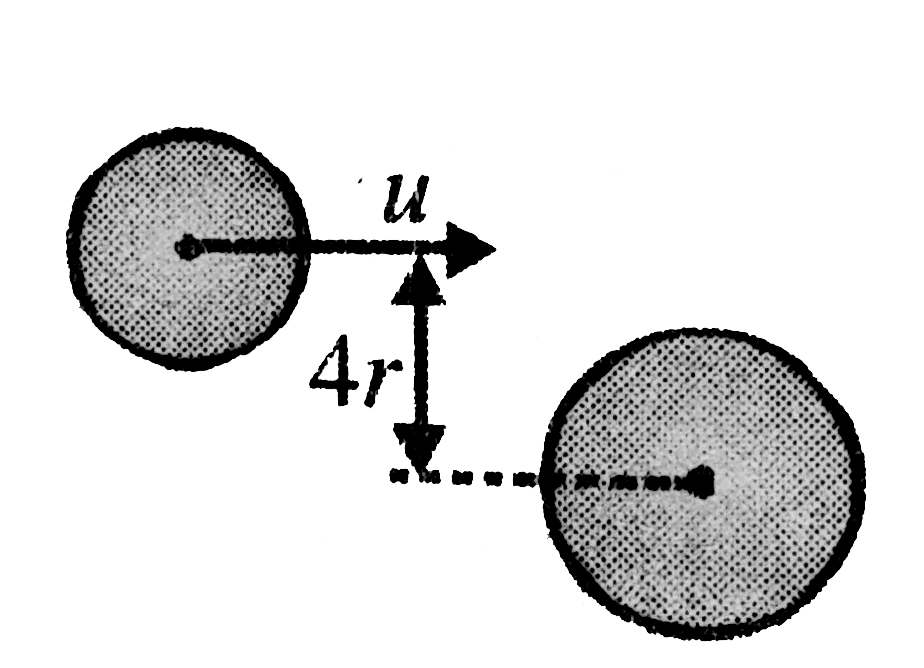
A circular disc of mass '2m' and radius '3r' is resting on a flat frictionless surface. Another circular disc of mass m and radius '2r', moving with a velocity 'u'. hits the first disc as shown in the figure. The collision is elastic.
 What is the final velocity of the heavier disc?
What is the final velocity of the heavier disc?
u5
2u5
3u5
4u5
The correct Answer is:B
Tangential component =usinθ=4u5
along normal velocity of m before collision:
u1=ucosθ=(3u)/5
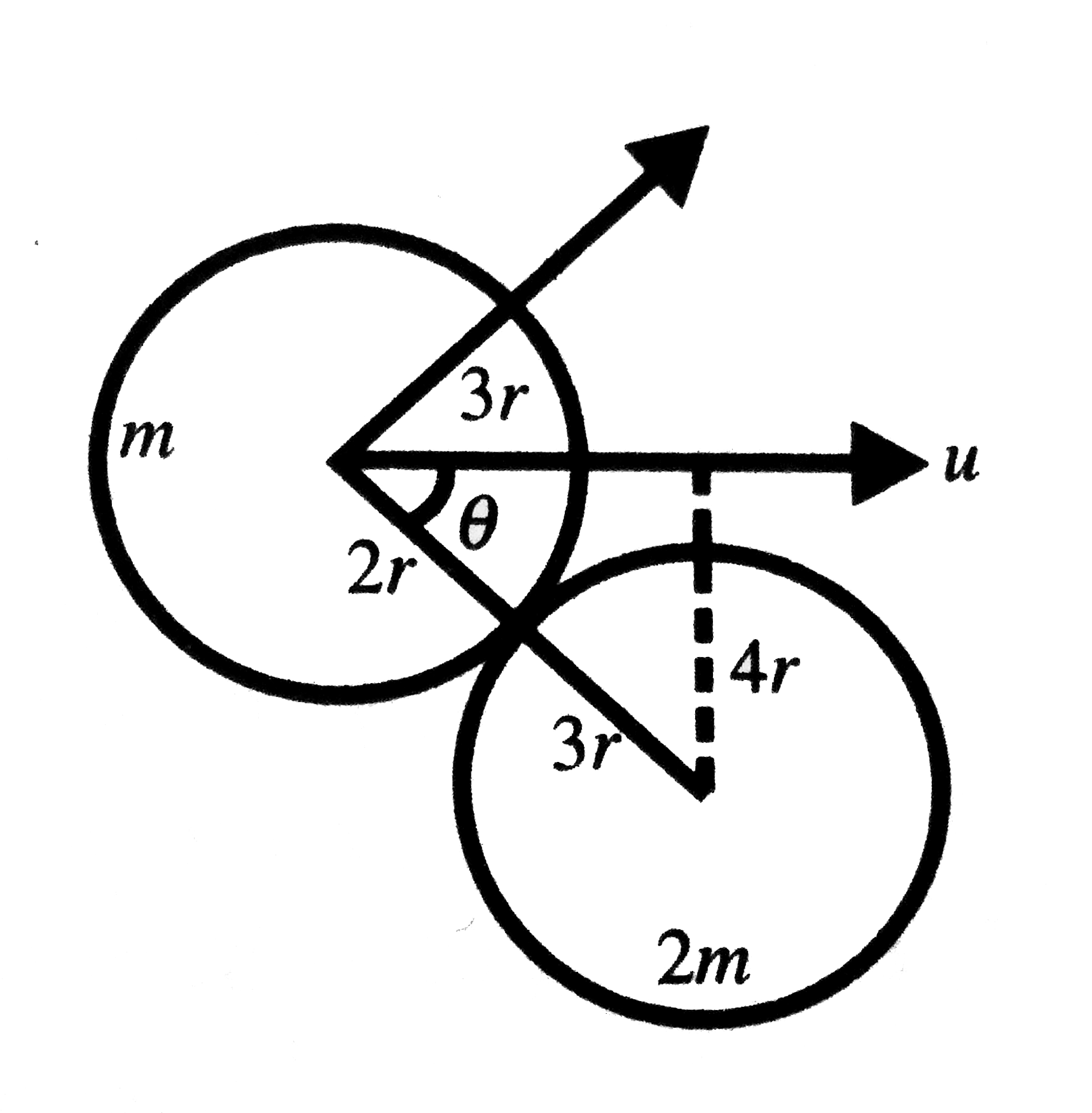
Along normal mv1+2mv2=mu1
v2−v1u1=1
solve to get v1=−u5,v2=2u5
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Integer
16 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
Knowledge Check
A circular disc of mass '2m' and radius '3r' is resting on a flat frictionless surface. Another circular disc of mass m and radius '2r', moving with a velocity 'u'. hits the first disc as shown in the figure. The collision is elastic.
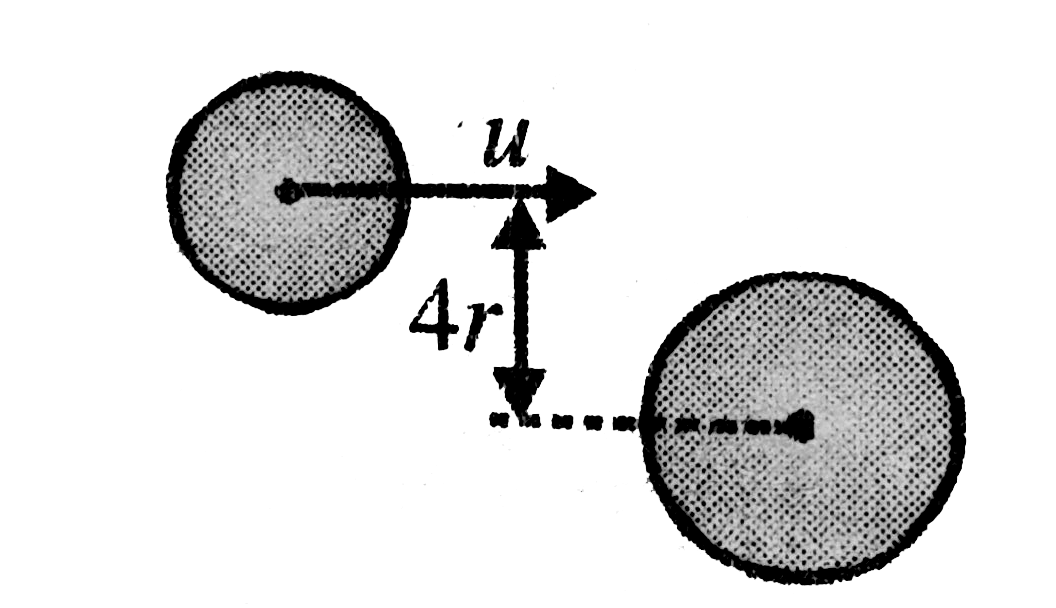
What is the tangential component of final velocity of the smaller disc?AuBu2C3u2D4u5A circular disc of mass '2m' and radius '3r' is resting on a flat frictionless surface. Another circular disc of mass m and radius '2r', moving with a velocity 'u'. hits the first disc as shown in the figure. The collision is elastic.
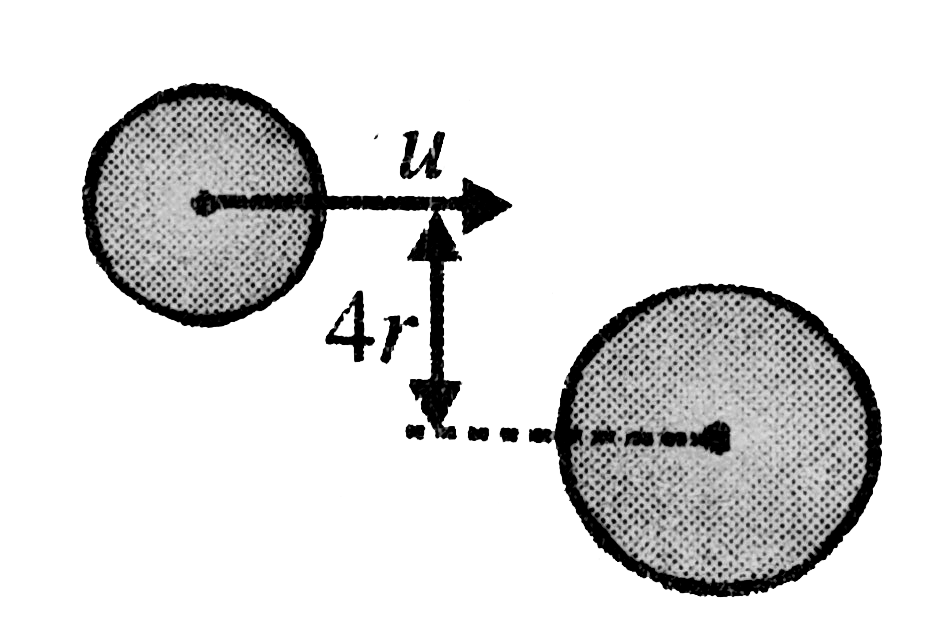
What is the magnitude of normal component of final velocity of the smaller disc'?Au5B2u512C3u5D4u5A circular disc of mass '2m' and radius '3r' is resting on a flat frictionless surface. Another circular disc of mass m and radius '2r', moving with a velocity 'u'. hits the first disc as shown in the figure. The collision is elastic.
 What is the final velocity of the heavier disc?A4v05Bv02C3v05D2v05
What is the final velocity of the heavier disc?A4v05Bv02C3v05D2v05
A circular disc is of mass M and radius r. From it a circualr piece is cut out with a radius of the disc as its diameter. Find the moment of inertia of the remainder about the axix of the disc
View SolutionA circular disc of mass 0.41 kg and radius 10 m rolls without slipping with a velocity of 2 m/s. The total kinetic energy of disc is
View SolutionA disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at tihe instant shows is
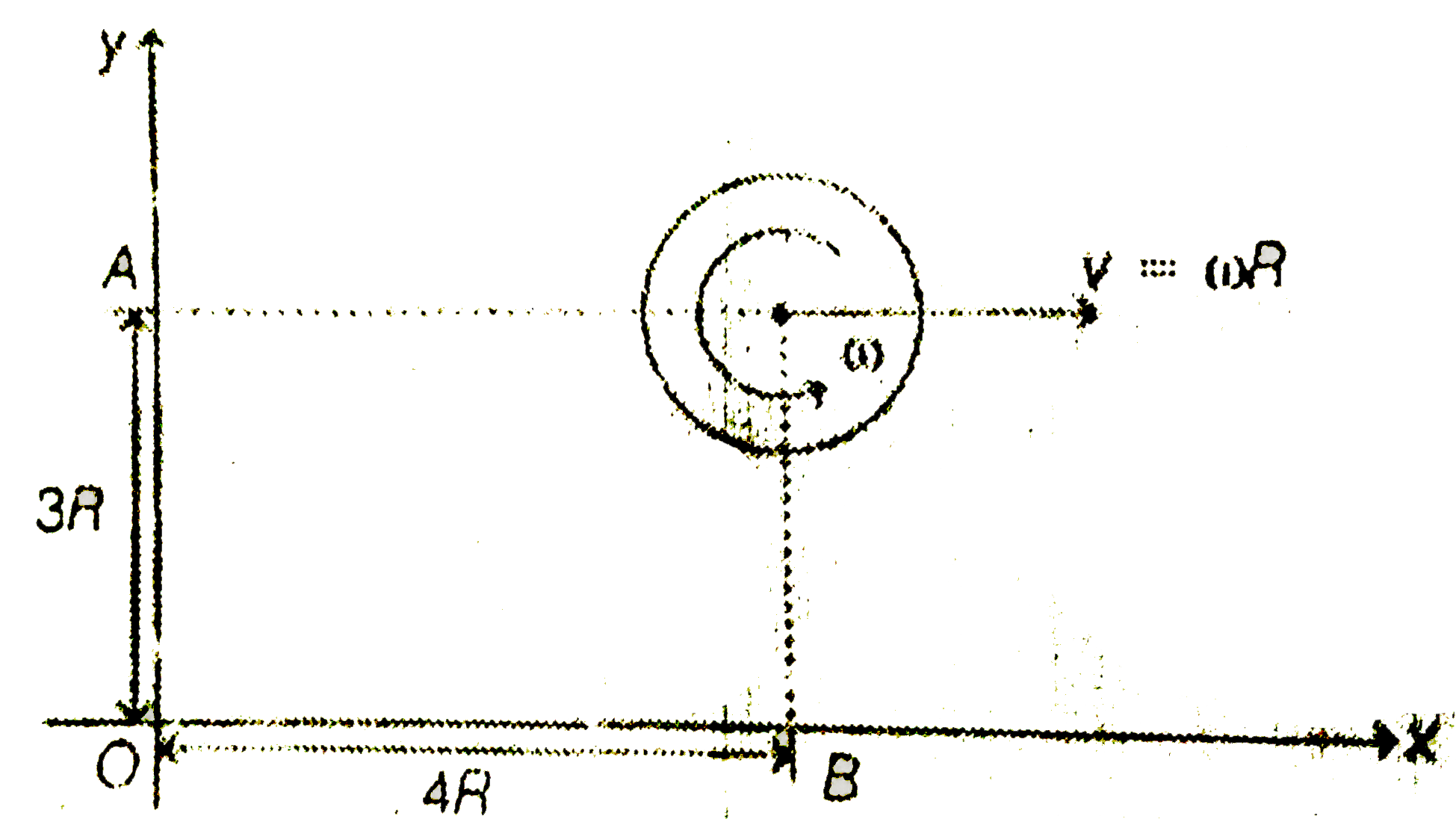
View SolutionA small smooth disc of mass m and radius moving with an initial velocity 'v' along the positive x− axis collided with a big disc of mass 2m and radius 2r which was initially at rest with its centre at origin as shown in figure.

If the coefficient of restitution is 0 then velocity of largen disc after collision is
View SolutionA point mass m collides with a disc of mass m and radius R resting on a rough horizontal surface as shown . Its collision is perfectly elastic. Find angular velocity of the disc after pure rolling starts

View Solution