A circular loop carrting a current a current I has wire of total length L. A uniform umagnetic field B exists parallel to the plane of the loop. (a ) find the trouque on the loop.(b) If the sme length of the wire is used to form a squar loop, what would be the torque? Which is larger?
To solve the problem, we will break it down into two parts as specified in the question.
Part (a): Finding the Torque on the Circular Loop
1. Identify the Length of the Circular Loop:
The total length of the wire used to form the circular loop is given as L. The circumference of a circular loop is given by:
L=2πR
where R is the radius of the circular loop.
2. Calculate the Radius:
Rearranging the equation for R:
R=L2π
3. Calculate the Area of the Circular Loop:
The area A of the circular loop can be calculated using the formula:
A=πR2
Substituting R:
A=π(L2π)2=πL24π2=L24π
4. Calculate the Torque:
The torque τ on a current-carrying loop in a magnetic field is given by:
τ=nBIAsinα
where n is the number of turns (which is 1 for a single loop), B is the magnetic field strength, I is the current, and α is the angle between the magnetic field and the area vector of the loop. Since the magnetic field is parallel to the plane of the loop, α=90∘ and sin90∘=1:
τ=BIA
Substituting the area A:
τ=BI(L24π)=BIL24π
Part (b): Finding the Torque on the Square Loop
1. Forming a Square Loop:
If the same length L of wire is used to form a square loop, the perimeter of the square loop is given by:
4s=L
where s is the side length of the square loop.
2. Calculate the Side Length:
Rearranging gives:
s=L4
3. Calculate the Area of the Square Loop:
The area A of the square loop is:
A=s2=(L4)2=L216
4. Calculate the Torque:
Using the same torque formula:
τ=BIA
Substituting the area A:
τ=BI(L216)=BIL216
Comparing the Torques
- Torque for the circular loop:
τcircle=BIL24π
- Torque for the square loop:
τsquare=BIL216
To compare which torque is larger, we can analyze the coefficients:
- 14π is approximately 0.0796
- 116=0.0625
Since 0.0796>0.0625, we conclude:
τcircle>τsquare
Final Answers:
(a) The torque on the circular loop is BIL24π.
(b) The torque on the square loop is BIL216. The torque on the circular loop is larger.
The total length of the wire used to form the circular loop is given as L. The circumference of a circular loop is given by:
L=2πR
where R is the radius of the circular loop.
Rearranging the equation for R:
R=L2π
The area A of the circular loop can be calculated using the formula:
A=πR2
Substituting R:
A=π(L2π)2=πL24π2=L24π
The torque τ on a current-carrying loop in a magnetic field is given by:
τ=nBIAsinα
where n is the number of turns (which is 1 for a single loop), B is the magnetic field strength, I is the current, and α is the angle between the magnetic field and the area vector of the loop. Since the magnetic field is parallel to the plane of the loop, α=90∘ and sin90∘=1:
τ=BIA
Substituting the area A:
τ=BI(L24π)=BIL24π
If the same length L of wire is used to form a square loop, the perimeter of the square loop is given by:
4s=L
where s is the side length of the square loop.
Rearranging gives:
s=L4
The area A of the square loop is:
A=s2=(L4)2=L216
Using the same torque formula:
τ=BIA
Substituting the area A:
τ=BI(L216)=BIL216
τcircle=BIL24π
- Torque for the square loop:
τsquare=BIL216
- 14π is approximately 0.0796
- 116=0.0625
τcircle>τsquare
(a) The torque on the circular loop is BIL24π.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - QUESTIONS FOR SHORT ASNWER10videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective29videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective 110videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer11videos
LIGHT WAVES
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer12videos
MAGNETIC FIELD DUE TO CURRENT
Similar Questions
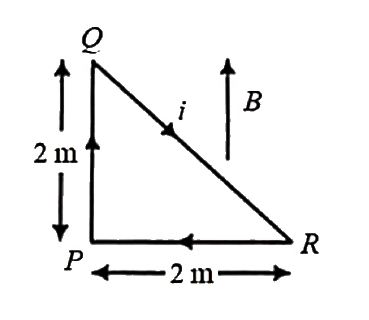
A loop PQR carries a current i=2A as shown in the figure. A uniform magnetic field B = 2T exists in space parallel to the plane of the loop . The magnetic torque on the loop is
 View Solution
View SolutionA circular loop of wire is carring a current i (as shown in the figure). On applying a uniform magnetic field inward perpendicular to the plane of the loop, the loop
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
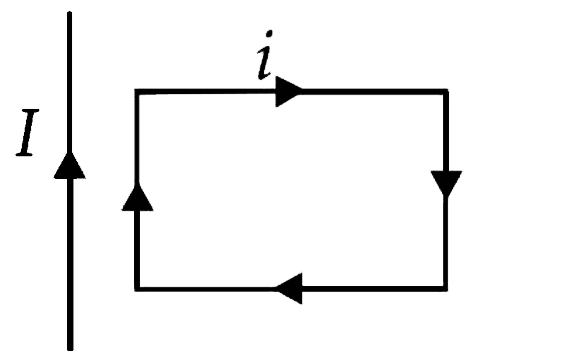
A rectangular loop carrying a current i is situated near a long straight wire such that the wire is parallel to one of the sides of the loop and is in the plane of the loop . If steady current I is established in the wire as shown in the figure ,
 Arotate about an axis parallel to the wireBmove away from the wireCmove towards the wireDremain stationary
Arotate about an axis parallel to the wireBmove away from the wireCmove towards the wireDremain stationary - Question 2 - Select One
A conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of loop. What is the magnetic force acting on the loop?
AI r BB2πrIBCzeroDπrIB
A square loop of sides 10cm carries a current of 10A.A uniform magnetic field of magnitude 0.20T exists parallel to one of the side of the loop.(a)What is the force acting on the loop? (b)What is the torque acting on the loop?
View SolutionA circular flexible loop of wire of radius r carrying a current I is placed in a uniform magnetic field B . If B is doubled, then tension in the loop
View SolutionA rectangular loop of sides 20 cm and 10 cm carries a current of 5.0 A. A uniform magnetic field of magnituded 0.20 T exists parallel ot the longer side of the loop (a) What is the force acting on the loop? (b) what is the torque acting on the loop?
View SolutionA triangular loop of side l carries a current I. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is
View SolutionA triangular loop of side l carries a current l. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is
View SolutionA conducting loop carrying a current I is placed in a uniform magnetic field ponting into the plane of the paper as shown. The loop will have a tendency to
 View Solution
View Solution

