A square loop of sides 10cm carries a current of 10A.A uniform magnetic field of magnitude 0.20T exists parallel to one of the side of the loop.(a)What is the force acting on the loop? (b)What is the torque acting on the loop?
The correct Answer is:A, B, C, D
To solve the problem step by step, we will calculate both the force acting on the loop and the torque acting on the loop.
Given Data:
- Side of the square loop, A=10cm=0.1m
- Current, I=10A
- Magnetic field, B=0.20T
Part (a): Calculating the Force Acting on the Loop
1. Identify the Length of the Side of the Loop:
The length of one side of the square loop is given as 10cm, which we convert to meters:
L=0.1m
2. Use the Formula for Force:
The force F acting on a current-carrying conductor in a magnetic field is given by:
F=I⋅B⋅L
where:
- I is the current,
- B is the magnetic field strength,
- L is the length of the conductor in the magnetic field.
3. Substituting the Values:
Now, substituting the values into the formula:
F=10A⋅0.20T⋅0.1m
4. Calculating the Force:
F=10⋅0.20⋅0.1=0.2N
Part (b): Calculating the Torque Acting on the Loop
1. Use the Formula for Torque:
The torque τ acting on a current loop in a magnetic field is given by:
τ=N⋅I⋅A⋅B⋅cos(θ)
where:
- N is the number of turns (for a single loop, N=1),
- A is the area of the loop,
- θ is the angle between the magnetic field and the normal to the plane of the loop.
2. Calculate the Area of the Loop:
The area A of the square loop is:
A=L2=(0.1m)2=0.01m2
3. Determine the Angle:
Since the magnetic field is parallel to one side of the loop, the angle θ between the magnetic field and the normal to the loop is 90∘. Thus, cos(90∘)=0.
4. Substituting the Values:
Now substituting the values into the torque formula:
τ=1⋅10A⋅0.01m2⋅0.20T⋅cos(0∘)
Note that since the magnetic field is parallel to one side of the loop, we should consider the effective area for torque calculation.
5. Calculating the Torque:
τ=10⋅0.01⋅0.20⋅1=0.02N m
Final Answers:
- (a) The force acting on the loop is 0.2N.
- (b) The torque acting on the loop is 0.02N m.
- Side of the square loop, A=10cm=0.1m
- Current, I=10A
- Magnetic field, B=0.20T
The length of one side of the square loop is given as 10cm, which we convert to meters:
L=0.1m
The force F acting on a current-carrying conductor in a magnetic field is given by:
F=I⋅B⋅L
where:
- I is the current,
- B is the magnetic field strength,
- L is the length of the conductor in the magnetic field.
Now, substituting the values into the formula:
F=10A⋅0.20T⋅0.1m
F=10⋅0.20⋅0.1=0.2N
The torque τ acting on a current loop in a magnetic field is given by:
τ=N⋅I⋅A⋅B⋅cos(θ)
where:
- N is the number of turns (for a single loop, N=1),
- A is the area of the loop,
- θ is the angle between the magnetic field and the normal to the plane of the loop.
The area A of the square loop is:
A=L2=(0.1m)2=0.01m2
Since the magnetic field is parallel to one side of the loop, the angle θ between the magnetic field and the normal to the loop is 90∘. Thus, cos(90∘)=0.
Now substituting the values into the torque formula:
τ=1⋅10A⋅0.01m2⋅0.20T⋅cos(0∘)
Note that since the magnetic field is parallel to one side of the loop, we should consider the effective area for torque calculation.
τ=10⋅0.01⋅0.20⋅1=0.02N m
- (a) The force acting on the loop is 0.2N.
- (b) The torque acting on the loop is 0.02N m.
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-1 PART-2
54 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-2 PART-1
15 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - PROBLEM
12 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
Similar Questions
A rectangular loop of sides 20 cm and 10 cm carries a current of 5.0 A. A uniform magnetic field of magnituded 0.20 T exists parallel ot the longer side of the loop (a) What is the force acting on the loop? (b) what is the torque acting on the loop?
View SolutionA square loop of side a carris a current I. The magnetic field at the centre of the loop is
View Solution
Knowledge Check
A conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of loop. What is the magnetic force acting on the loop?
AI r BB2πrIBCzeroDπrIB
A square loop of side 6cm carries a current of 30A. Calculate the magnitude of magnetic field B at a point P lying on the axis of the loop and a distance√7 cm from centre of the loop.
View SolutionA current loop, carrying a current of 5.0 A, is in the shape of a right triangle with sides 30,40, and 50 cm. The loop is in a uniform magnetic field of magnitude 80 mT whose direction is parallel to the current in the 50 cm side of the loop. Find the magnitude of (a) the magnetic dipole moment of the loop and (b) the torque on the loop.
View SolutionA loop PQR carries a current i=2A as shown in the figure. A uniform magnetic field B = 2T exists in space parallel to the plane of the loop . The magnetic torque on the loop is
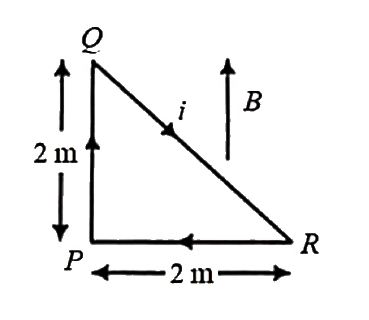
View SolutionA wire is bent in the form of an equilateral triangle PQR of side 10 cm and carries a current of 5.0 A. It is placed in a magnetic field B of magnitude 2.0 T directed perpendicularly to the plane of the loop. Find the forces on the three sides of the triangle.
View SolutionTorque acting on a current loop in a uniform magnetic field is equal to
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
View SolutionA circular loop carrting a current a current I has wire of total length L. A uniform umagnetic field B exists parallel to the plane of the loop. (a ) find the trouque on the loop.(b) If the sme length of the wire is used to form a squar loop, what would be the torque? Which is larger?
View Solution
