A circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform. Now the platform is given an angular velocity . When the tortoise move along a chord of the platform with a constant velocity (with respect to the platform),
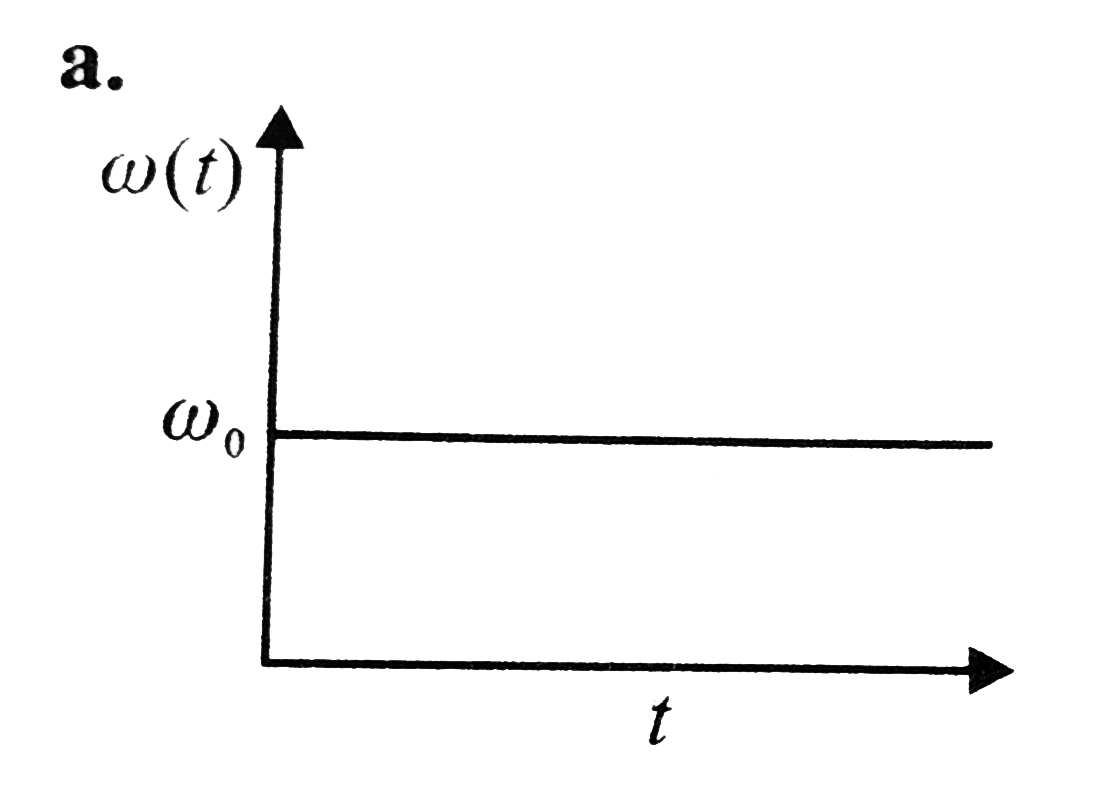
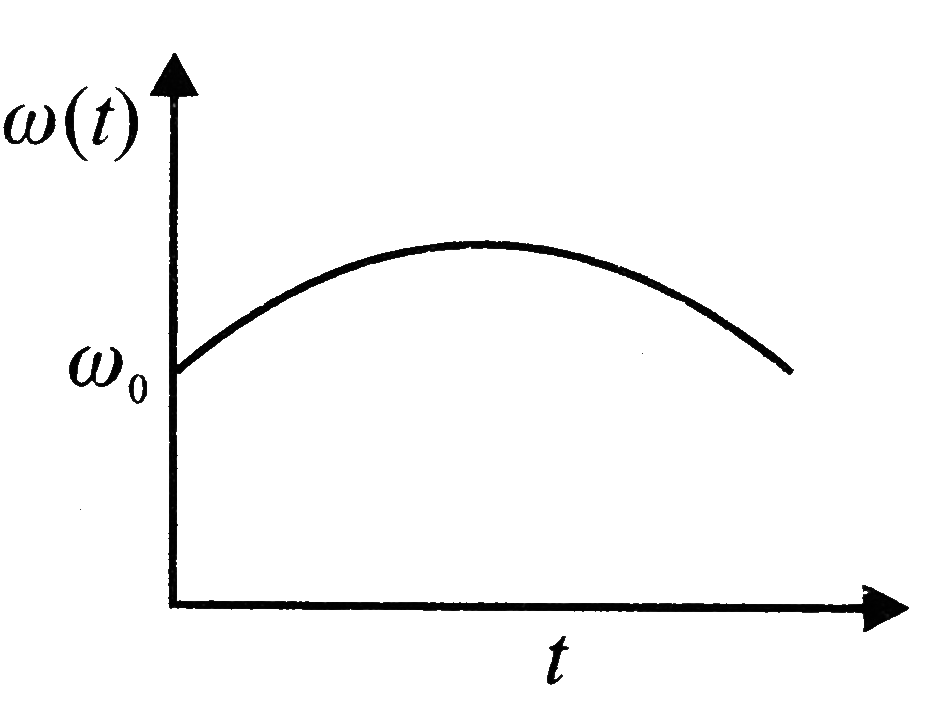
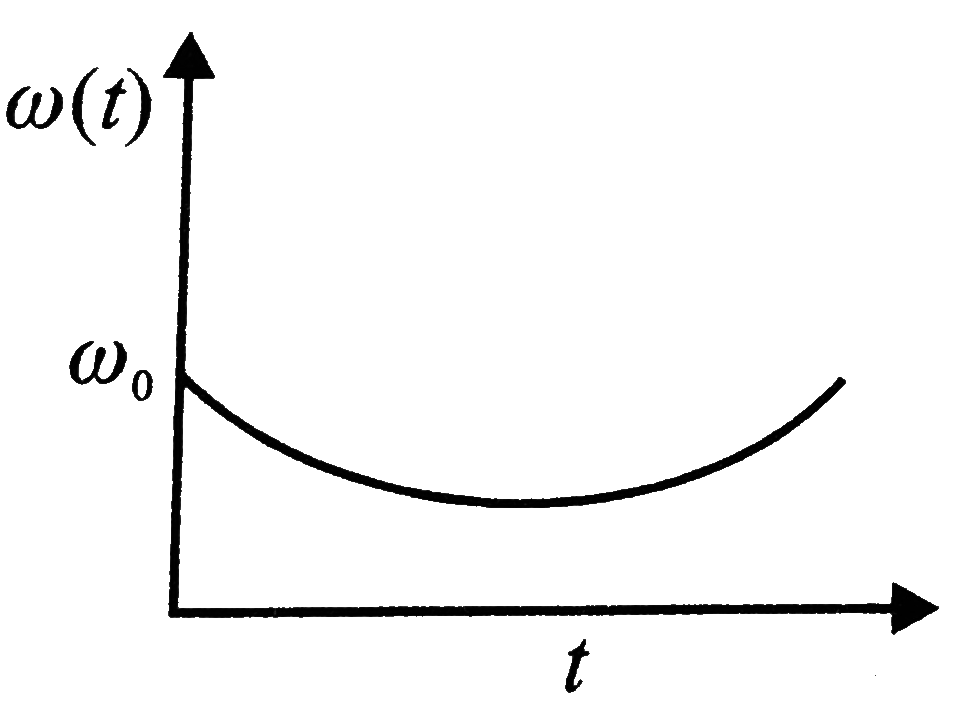
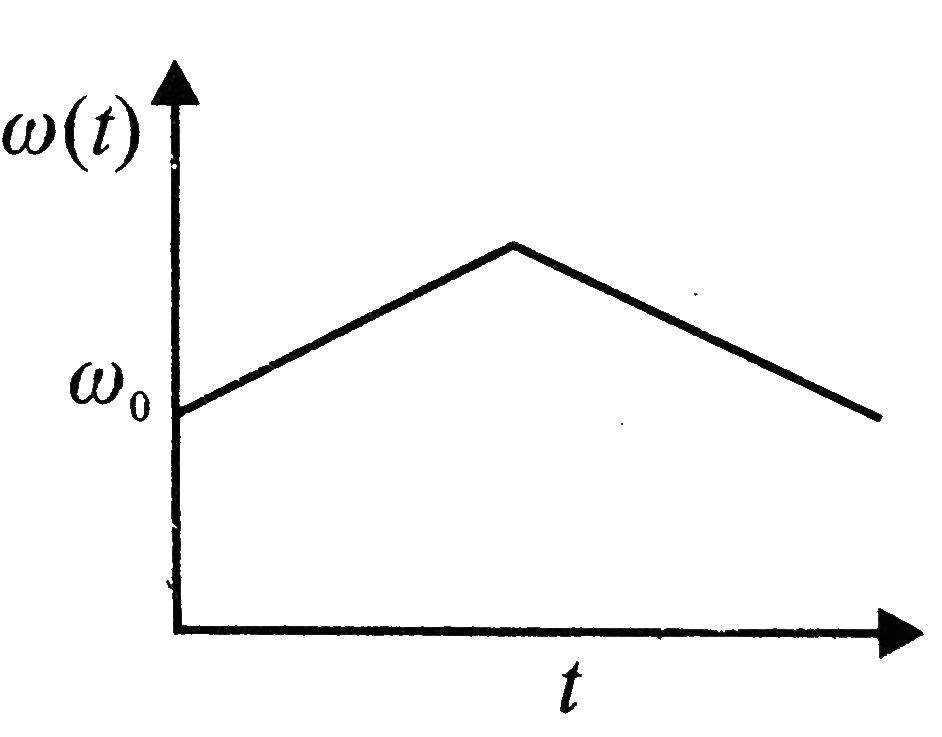
The correct Answer is:B
To solve the problem, we need to analyze the motion of the tortoise on the rotating platform and how it affects the angular velocity of the system. Here’s a step-by-step breakdown of the solution:
Step 1: Understanding the System
The system consists of a circular platform rotating with an initial angular velocity ω0. A tortoise is sitting at the edge of the platform and moves along a chord with a constant velocity v relative to the platform.
Step 2: Angular Momentum Conservation
Since there are no external torques acting on the system, the angular momentum of the system must be conserved. The total angular momentum L can be expressed as:
L=Iplatform⋅ω+Itortoise⋅ω
where Iplatform is the moment of inertia of the platform, Itortoise is the moment of inertia of the tortoise, and ω is the angular velocity of the system at any time.
Step 3: Moment of Inertia
The moment of inertia of the tortoise changes as it moves along the chord. If the tortoise is at a distance r from the center of the platform, the moment of inertia of the tortoise can be expressed as:
Itortoise=m⋅r2
where m is the mass of the tortoise.
Step 4: Relationship Between Angular Velocity and Moment of Inertia
From the conservation of angular momentum, we have:
Iplatform⋅ω0+Itortoise⋅ω0=Iplatform⋅ω+Itortoise⋅ω
This implies that as the tortoise moves and changes its distance r, the angular velocity ω must adjust to conserve angular momentum.
Step 5: Analyzing the Motion
1. When the tortoise is at the edge of the platform, r is maximum, and thus Itortoise is maximum. This results in a minimum angular velocity ω.
2. As the tortoise moves towards the center, r decreases, which decreases Itortoise and increases ω.
3. When the tortoise reaches the center, Itortoise is at its minimum, resulting in a maximum angular velocity ω.
4. As the tortoise moves back towards the edge, Itortoise increases again, leading to a decrease in ω.
Step 6: Conclusion
The relationship between angular velocity ω and the position of the tortoise shows that ω will have a minimum value when the tortoise is at the edge, a maximum value when it is at the center, and then decrease again as it moves back to the edge. This results in a graph of ω versus the position of the tortoise that is a wave-like function, indicating the minimum and maximum values.
Final Answer
The correct option representing the relationship between angular velocity ω and the position of the tortoise is option C.
---
The system consists of a circular platform rotating with an initial angular velocity ω0. A tortoise is sitting at the edge of the platform and moves along a chord with a constant velocity v relative to the platform.
Since there are no external torques acting on the system, the angular momentum of the system must be conserved. The total angular momentum L can be expressed as:
L=Iplatform⋅ω+Itortoise⋅ω
where Iplatform is the moment of inertia of the platform, Itortoise is the moment of inertia of the tortoise, and ω is the angular velocity of the system at any time.
The moment of inertia of the tortoise changes as it moves along the chord. If the tortoise is at a distance r from the center of the platform, the moment of inertia of the tortoise can be expressed as:
Itortoise=m⋅r2
where m is the mass of the tortoise.
From the conservation of angular momentum, we have:
Iplatform⋅ω0+Itortoise⋅ω0=Iplatform⋅ω+Itortoise⋅ω
This implies that as the tortoise moves and changes its distance r, the angular velocity ω must adjust to conserve angular momentum.
1. When the tortoise is at the edge of the platform, r is maximum, and thus Itortoise is maximum. This results in a minimum angular velocity ω.
2. As the tortoise moves towards the center, r decreases, which decreases Itortoise and increases ω.
3. When the tortoise reaches the center, Itortoise is at its minimum, resulting in a maximum angular velocity ω.
4. As the tortoise moves back towards the edge, Itortoise increases again, leading to a decrease in ω.
The relationship between angular velocity ω and the position of the tortoise shows that ω will have a minimum value when the tortoise is at the edge, a maximum value when it is at the center, and then decrease again as it moves back to the edge. This results in a graph of ω versus the position of the tortoise that is a wave-like function, indicating the minimum and maximum values.
The correct option representing the relationship between angular velocity ω and the position of the tortoise is option C.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - MCQ_TYPE
14 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - AR_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - True/False
4 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A uniform horizontal circular platform of mass 200kg is rotating at 5 rpm about vertical axis passing through its centre. A boy of mass 80kg is standing at its edge. if boy moves to centre of platform, find out final angular speed
View SolutionA horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
View Solution
A uniform rod of length L is free to rotate in a vertical plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given as
View Solution
A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given as
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
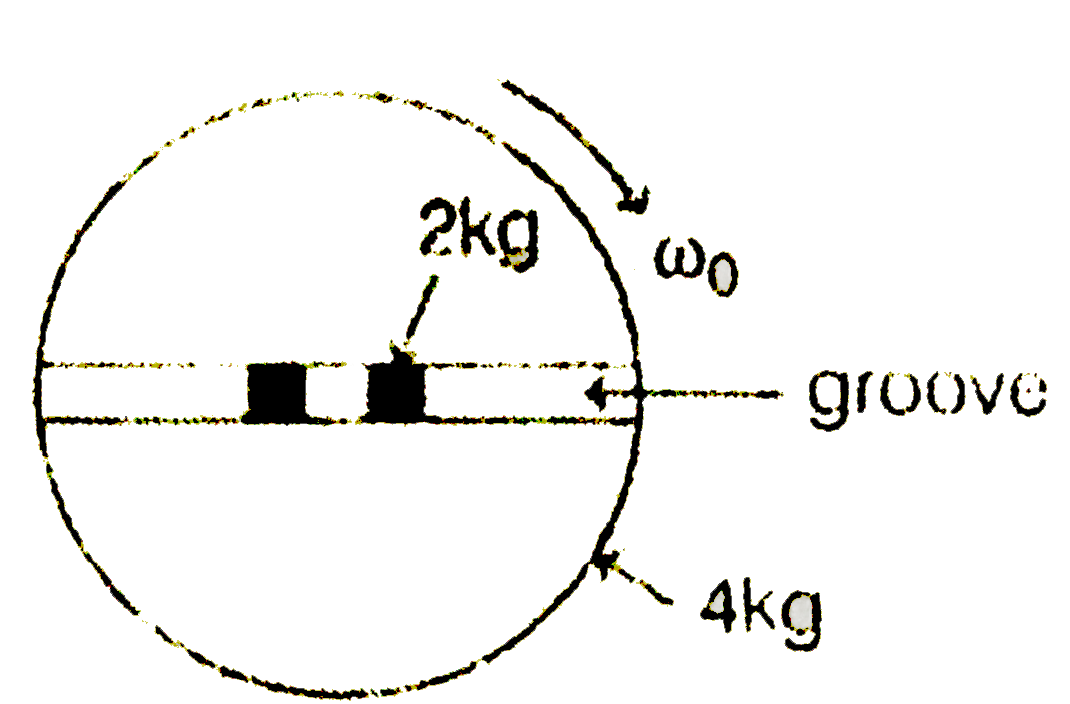
View SolutionA disc of mass 4 kg and radius 6 metre is free to rotate in horizontal plane about a vertical fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small blocks of masses 2 kg each are placed in it on either side of the centre of the disc as shown in figure. The disc is given initial angular velocity ω0 =12 rad/sec and released. Find the angular speed of disc (in radian/sec) when the blocks reach the ends of the disc.
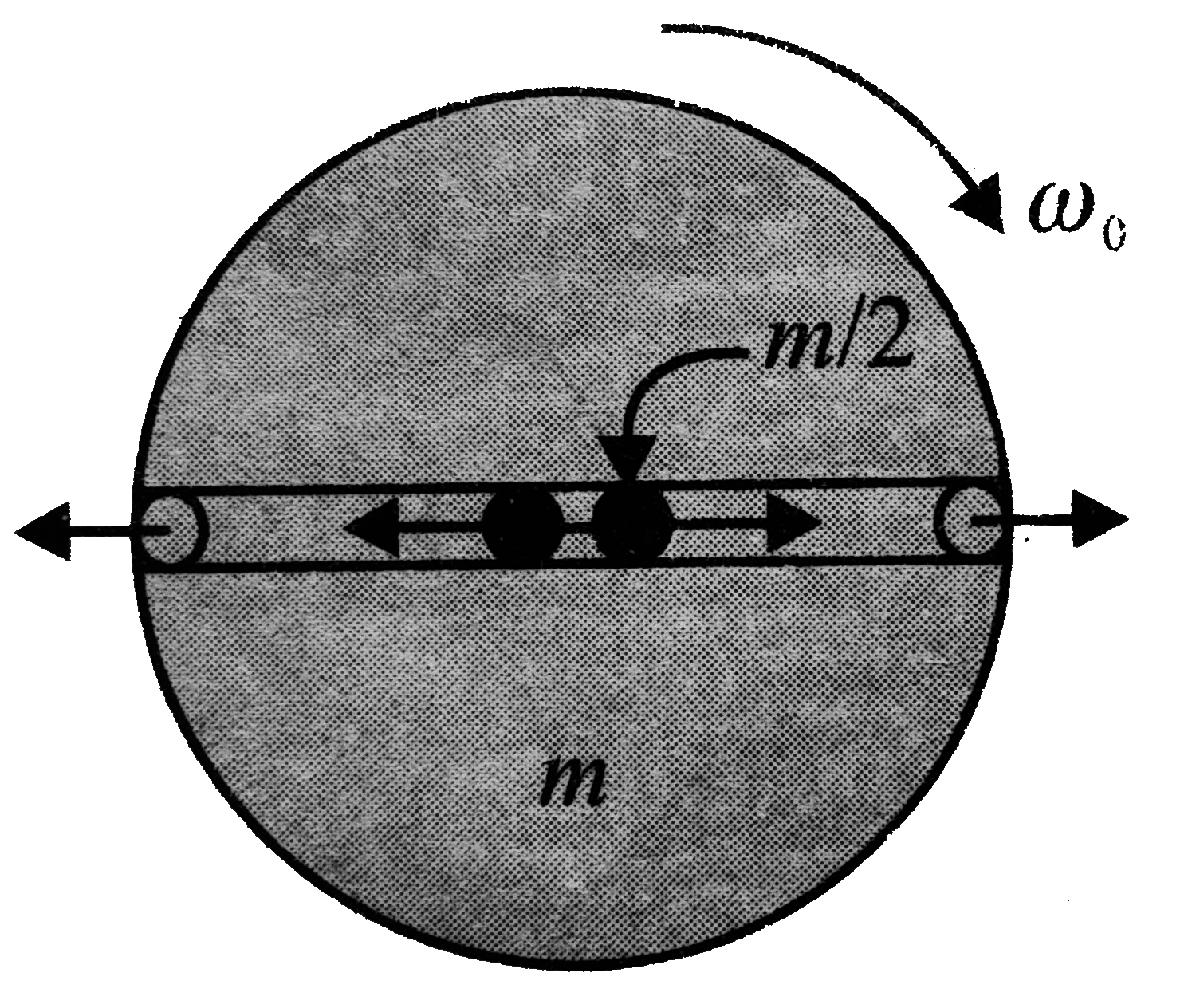
View SolutionA disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity ω0 and released.

The angular speed of the disc when the balls reach the end of the disc is
View SolutionA uniform rod of mass m and length L is free to rotate in the vertical plane about a horizontal axis passing through its end. The rod initially in horizontal position is released. The initial angular acceleration of the rod is:

View SolutionA disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity ω0 and released.

The speed of each ball relative to the ground just after they leave the disc is
View SolutionA thin horizontal circular disc is roating about a vertical axis passing through its centre. An insect is at rest at a point near the rim of the disc. The insect now moves along a diameter of the disc to reach its other end. During the journey of the insect, the angular speed of the disc.
View Solution
