A circular ring of mass 6kg and radius a is placed such that its center of lies at the origin. Two particles of masses 2 kg each are placed at the intersecting points of the circle with positive X-axis and positive Y-axis. Then, the angle made by the position vector of center of mass of entire system with X-axis is
45∘
60∘
tan−(45)
30∘
The correct Answer is:A
To solve the problem of finding the angle made by the position vector of the center of mass of the entire system with the X-axis, we can follow these steps:
Step 1: Identify the masses and their positions
- We have a circular ring of mass m1=6kg located at the origin (0, 0).
- There are two particles, each of mass m2=2kg, placed at the points where the circle intersects the positive X-axis and positive Y-axis:
- Particle 2 is at (a,0) (on the positive X-axis).
- Particle 3 is at (0,a) (on the positive Y-axis).
Step 2: Write down the coordinates of the center of mass
The center of mass (Xcm,Ycm) of the system can be calculated using the formula:
Xcm=m1x1+m2x2+m3x3m1+m2+m3
Ycm=m1y1+m2y2+m3y3m1+m2+m3
Step 3: Substitute the values into the formulas
- For the X-coordinates:
- x1=0 (ring at origin)
- x2=a (particle 2)
- x3=0 (particle 3)
Xcm=6⋅0+2⋅a+2⋅06+2+2=2a10=a5
- For the Y-coordinates:
- y1=0 (ring at origin)
- y2=0 (particle 2)
- y3=a (particle 3)
Ycm=6⋅0+2⋅0+2⋅a6+2+2=2a10=a5
Step 4: Calculate the angle θ
The angle θ made by the position vector of the center of mass with the X-axis can be found using:
tanθ=YcmXcm=a5a5=1
Step 5: Find θ
Since tanθ=1:
θ=tan−1(1)=45∘
Final Answer
The angle made by the position vector of the center of mass of the entire system with the X-axis is 45∘.
---
- We have a circular ring of mass m1=6kg located at the origin (0, 0).
- There are two particles, each of mass m2=2kg, placed at the points where the circle intersects the positive X-axis and positive Y-axis:
- Particle 2 is at (a,0) (on the positive X-axis).
- Particle 3 is at (0,a) (on the positive Y-axis).
The center of mass (Xcm,Ycm) of the system can be calculated using the formula:
Xcm=m1x1+m2x2+m3x3m1+m2+m3
Ycm=m1y1+m2y2+m3y3m1+m2+m3
- For the X-coordinates:
- x1=0 (ring at origin)
- x2=a (particle 2)
- x3=0 (particle 3)
Xcm=6⋅0+2⋅a+2⋅06+2+2=2a10=a5
- y1=0 (ring at origin)
- y2=0 (particle 2)
- y3=a (particle 3)
The angle θ made by the position vector of the center of mass with the X-axis can be found using:
tanθ=YcmXcm=a5a5=1
Since tanθ=1:
θ=tan−1(1)=45∘
The angle made by the position vector of the center of mass of the entire system with the X-axis is 45∘.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason
21 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Match the coloumns
9 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Check points
50 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
Two particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
View SolutionTwo particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
View SolutionFour particles, each of mass 1kg, are placed at the corners of a square OABC of side 1m. 'O' is at the origin of the coordinate system. OA and OC are aligned along positive x-axis and positive y-axis respectively. The position vector of the centre of mass is (in 'm')
View SolutionThree charges +q,−q,and+2q are placed at the verticles of a right angled triangle (isoceles triangle) as shown. The net electrostatic energy of the configuration is :

View SolutionA circular ring of mass M and radius 'a' is placed in a gravity free space. A small particle of mass m placed on the axis of the ring at a distance √3a from the center of the ring, is released from rest. The velocity with which the particle passes through the center of the ring is
View SolutionIf a line makes an angle of π4 with the positive directions of each of x-axis and y-axis, then the angle that the line makes with the positive direction of z-axis is
View SolutionThree rings each of mass m and radius r are so placed that they touch each other. The radius of gyration of the system about the axis as shown in the figure is
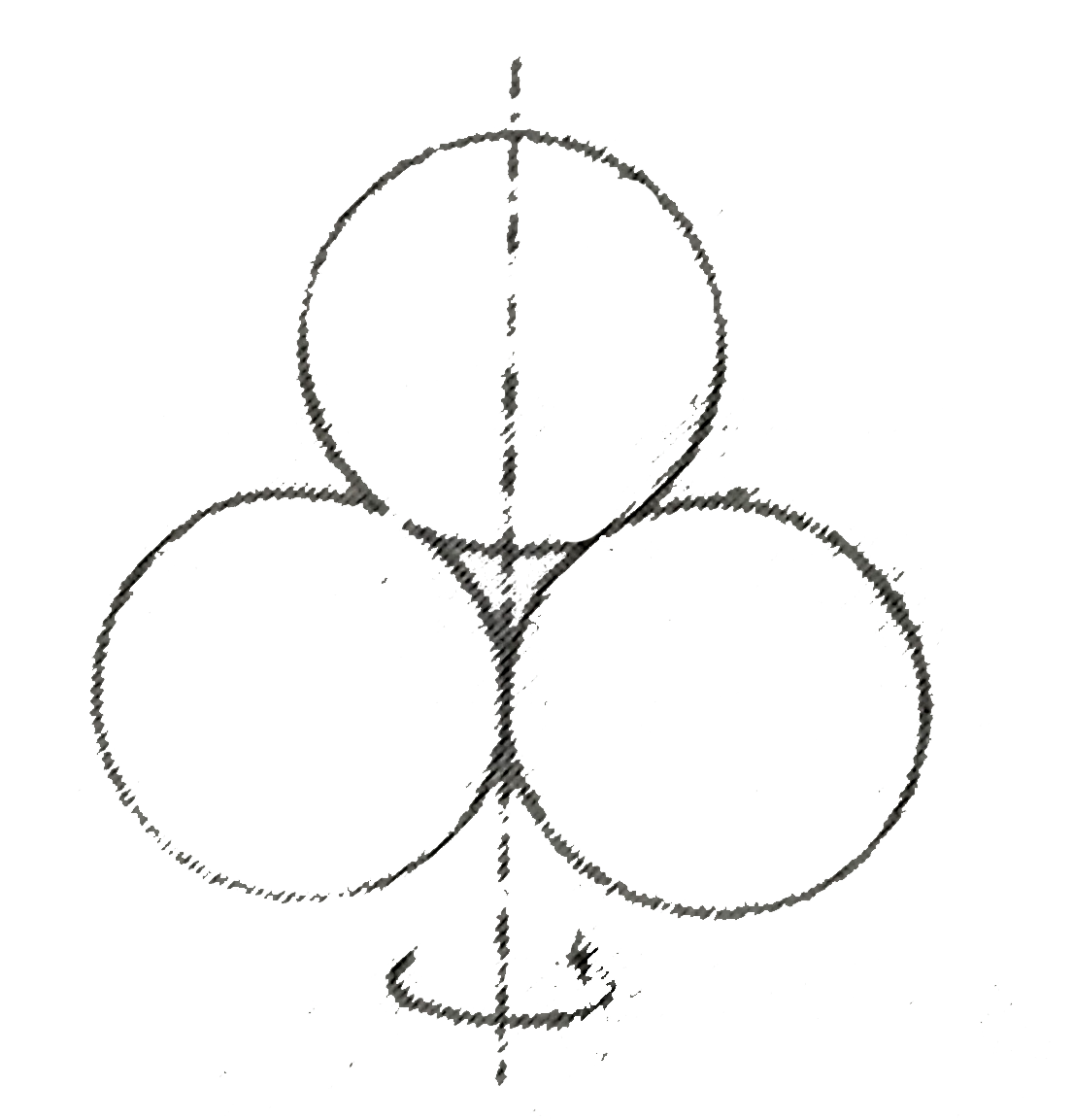
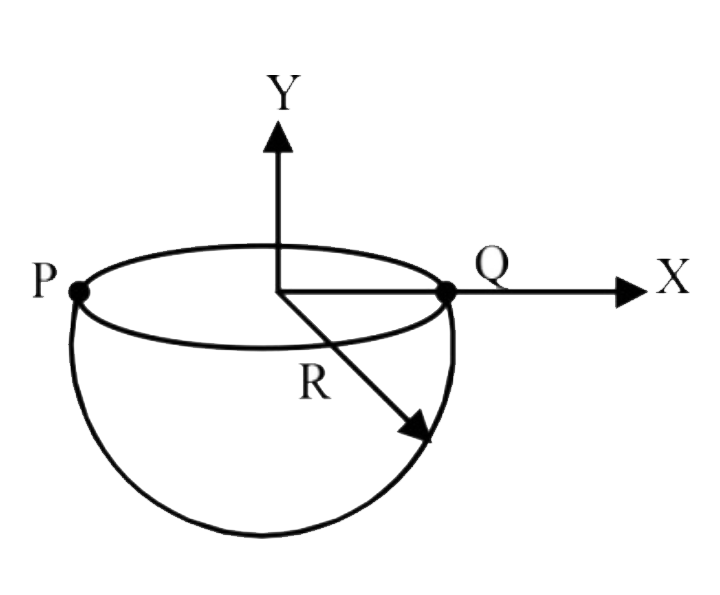
View SolutionA hollow hemisphere of mass 4m is placed as shown in figure . Two point masses m each are fixed to it at points P and Q on diametrically opposite points. The position of center of mass of the system is
View SolutionFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A, B, C and D of a square of side 1m. Find the position of centre of mass of the particles.
View SolutionFind the equation of the circle whose radius is 5 and centre lies on the positive side of x-axis at a distance 5 from the origin.
View Solution
