A clear transparent glass sphere (μ=1.5) of radius R is immersed in a liquid of refractive index 1.25. A parallel beam of light incident on it will converge to a point. The distance of this point from the center will be
−3R
+3R
−R
+R
The correct Answer is:b.
To solve the problem, we will use the lens maker's formula for a spherical interface between two media. The formula is given by:
μ1v−μ2u=μ2−μ1R
Where:
- μ1 is the refractive index of the medium from which light is coming (in this case, the liquid, μ1=1.25)
- μ2 is the refractive index of the glass sphere (μ2=1.5)
- R is the radius of curvature of the spherical surface (for a sphere, R=R)
- u is the object distance (for parallel rays, u=−∞)
- v is the image distance from the center of the sphere
Step 1: Substitute the known values into the lens maker's formula
Given that the rays are parallel, we can set u=−∞. Therefore, the lens maker's formula simplifies to:
1.25v−1.5−∞=1.5−1.25R
Since 1.5−∞=0, the equation reduces to:
1.25v=0.25R
Step 2: Solve for v
Rearranging the equation gives:
v=1.25R0.25=5R
Step 3: Consider the distance from the center of the sphere
Since v=5R is the distance from the center of the sphere to the image point, we need to find the distance from the center of the sphere to the point where the light converges.
Step 4: Calculate the total distance
The total distance from the center of the sphere to the point where the light converges is 5R.
Final Answer
Thus, the distance of the point from the center of the sphere is:
Distance from center=5R
---
- μ1 is the refractive index of the medium from which light is coming (in this case, the liquid, μ1=1.25)
- μ2 is the refractive index of the glass sphere (μ2=1.5)
- R is the radius of curvature of the spherical surface (for a sphere, R=R)
- u is the object distance (for parallel rays, u=−∞)
- v is the image distance from the center of the sphere
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension
51 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective
26 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
A lens is made of flint glass (refractive index =1.5). When the lens is immersed in a liquid of refractive index 1.25 , the focal length:
View SolutionThe refractive index of glass is 1.5. The speed of light in glass is
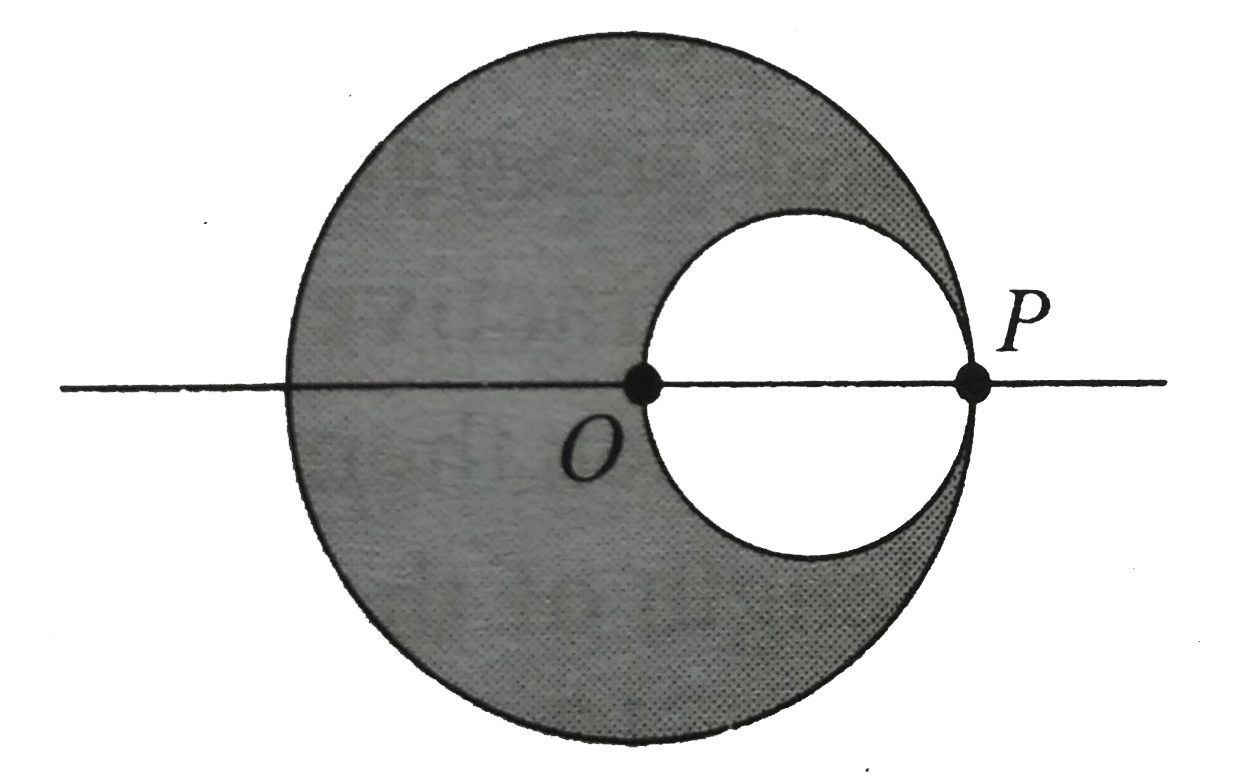
View SolutionA transparent sphere of radius R ahs a cavity of radius R/2 as shown in figure,. Find the refractive index of the sphere if a parallel beam of light falling on left sureface focuses at point P.
View SolutionRefractive index of the material of concave lens is μ. The lens is immersed inb a medium of refractive index μ1(μ1>μ). A parallel beam of light is incident on the lens. Draw a diagram to show the path of emergent rays.
View SolutionA thin convergent glass lens (μg=1.5) has a power of +5.0D. When this lens is immersed in a liquid of refractive index μ1, it acts as a divergent lens of focal length 100cm. The value of μ1 is
View SolutionA thin convergent glass lens (μg=1.5) has a power of +5.0D. When this lens is immersed in a liquid of refractive index μ1, it acts as a divergent lens of focal length 100cm. The value of μ1 is
View SolutionA glass prism of refractive index 1.5 is immersed in water of refractive index 4/3. A light ray incident normally on face AB is totally reflected at face AC if

View SolutionThe refractive index of glass is 1.5. Find the speed of light in glass.
View SolutionA transparent cube of side d, made of a material of refractive index μ2 , is immersed in a liquid of refractive index μ1(μ1<μ2). . A ray is incident on the face AV at an angle θ (shown in the figure). Total internal refraction takes place at point E on the face BC. Then must satisfy:
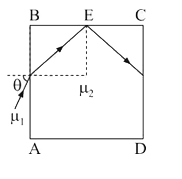
View SolutionA transparent cube of side d, made of a material of refractive index μ2 , is immersed in a liquid of refractive index μ1(μ1<μ2). . A ray is incident on the face AV at an angle θ (shown in the figure). Total internal refraction takes place at point E on the face BC. Then must satisfy:

View Solution
