In a slide show programme, the image on the screen has an area 900times that of the slide. If the distance between the slide and the screen is x times the distance between the slide and the projector lens, then
x=30
x=31
x=500
x=1/30
The correct Answer is:b.
To solve the problem, we need to analyze the relationship between the areas of the slide and the image on the screen, the magnification, and the distances involved in the projection setup.
1. Understanding the Areas:
- Let the area of the slide be A.
- The area of the image on the screen is given as 900A.
2. Finding the Magnification of Area:
- The magnification of area is defined as the ratio of the area of the image to the area of the object (slide).
- Therefore, the magnification of area Ma can be expressed as:
Ma=Area of ImageArea of Slide=900AA=900
3. Finding Linear Magnification:
- The linear magnification m is related to the magnification of area by the square root:
m=√Ma=√900=30
4. Defining Distances:
- Let the distance between the slide and the projector lens be n.
- The distance between the projector lens and the screen, based on the linear magnification, is:
V=m⋅n=30n
5. Calculating the Total Distance:
- The total distance between the slide and the screen is the sum of the distance from the slide to the projector and from the projector to the screen:
Distance between slide and screen=n+30n=31n
6. Relating to the Given Ratio:
- The problem states that the distance between the slide and the screen is x times the distance between the slide and the projector lens. Therefore:
x⋅n=31n
- Dividing both sides by n (assuming n≠0):
x=31
Final Answer:
The value of x is 31.
- Let the area of the slide be A.
- The area of the image on the screen is given as 900A.
- The magnification of area is defined as the ratio of the area of the image to the area of the object (slide).
- Therefore, the magnification of area Ma can be expressed as:
Ma=Area of ImageArea of Slide=900AA=900
- The linear magnification m is related to the magnification of area by the square root:
m=√Ma=√900=30
- Let the distance between the slide and the projector lens be n.
- The distance between the projector lens and the screen, based on the linear magnification, is:
V=m⋅n=30n
- The total distance between the slide and the screen is the sum of the distance from the slide to the projector and from the projector to the screen:
Distance between slide and screen=n+30n=31n
- The problem states that the distance between the slide and the screen is x times the distance between the slide and the projector lens. Therefore:
x⋅n=31n
- Dividing both sides by n (assuming n≠0):
x=31
The value of x is 31.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig2videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension51videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective26videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.315videos
ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
Similar Questions
The image of a candle flame formed by a lens is obtained on a screen placed on the other side of the lens. If the image is three times the size of the flame and the distance between lens and image is 80cm, at what distance should the candle be placed from the lens ? What is the nature of the image at a distance of 80cm from the lens ?
View SolutionA lens forms a sharp image on a screen. On inserting a parallel sided glass slab between the lens and the screen, it is found necessary to move the screen a distance d away the lens in order for the image to be sharp again. If the refractive index of the material of the slab is μ, the thickness of the slab is
View Solution
Knowledge Check
- Question 1 - Select One
In a double slit experiment, the distance between slits in increased ten times whereas their distance from screen is halved then the fringe width is
Abecomes 120Bbecomes 190Cit remains sameDbecomes 110
The distance between an object and a screen is 100 cm. A lens can produce real image of the object on the screen for two different position between the screen and the object. The distance between these two positions is 40 cm. If the power of the lens is close to (N100)D where N is integer, the value of N is ___________.
View SolutionA wire is sliding as shown in Figure. The angle between the acceleration and the velocity of the wire is
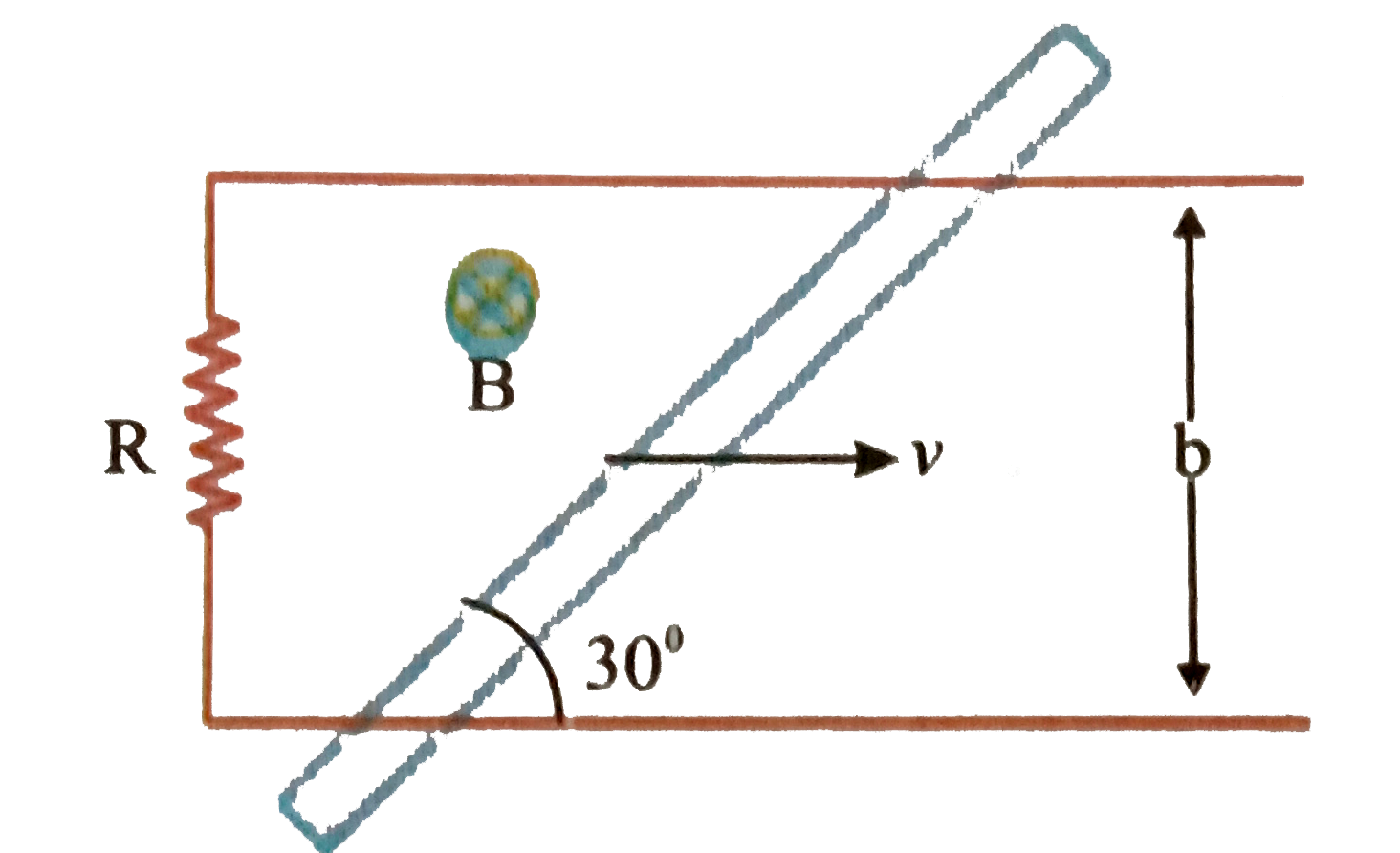 View Solution
View SolutionIn may experimental set-ups the source and screen are fixed at a distance say D and the lens is movable. Show that there are two positions for the lens for which an image is formed on the screen. Find the distance between these points and the ratio of the image sizes for these two points.
View SolutionA convex lens of focal length f is placed somewhere in between an object and a screen. The distance between the object and the screen is x. If the numerical value of the magnification produced by the lens is m, then the focal lnegth oof the lens is .
View SolutionA body slides down a smooth plane starting from rest in 4sec. Time taken to slide first 1/4 of the distance is
View SolutionAn image of a bright square is obtained on a screen with the aid of a convergent lens. The distance between the square and the lens is 40cm. The area of the image is nine times larger than that of the square. Select the correct statement(s):
View SolutionA convex lens forms an image of an object on a screen. The height of the image is 9 cm . The lens is now displaced until an image is again obtained on the screen. Then height of this image is 4 cm . The distance between the object and the screen is 90 cm.
View Solution

