Refractive index of the material of concave lens is μ. The lens is immersed inb a medium of refractive index μ1(μ1>μ). A parallel beam of light is incident on the lens. Draw a diagram to show the path of emergent rays.
To solve the problem, we need to analyze the behavior of light rays as they pass through a concave lens that is immersed in a medium with a higher refractive index than the lens itself. Let's break down the solution step by step:
Step 1: Understanding the Setup
We have a concave lens with a refractive index μ, and it is immersed in a medium with a refractive index μ1 where μ1>μ. A parallel beam of light is incident on the lens.
Hint: Remember that the refractive index determines how light bends as it passes through different media.
Step 2: Drawing the Lens
Draw a concave lens. The lens has two curved surfaces. Label the lens with its principal axis. The left side of the lens is where the light rays will be incident.
Hint: A concave lens is thinner in the middle and thicker at the edges.
Step 3: Incident Rays
Draw two parallel lines representing the incident rays approaching the lens. These lines should be parallel to the principal axis of the lens.
Hint: The incident rays represent a parallel beam of light, which is a common scenario in optics.
Step 4: Refraction at the First Surface
When the parallel rays hit the first surface of the concave lens, they will refract. Since the lens has a lower refractive index than the surrounding medium, the rays will bend away from the normal.
Hint: Use Snell's law to understand how light bends when it moves from a medium of higher refractive index to one of lower refractive index.
Step 5: Refraction at the Second Surface
After passing through the lens, the rays will hit the second surface. As they exit the lens into the medium with a higher refractive index, they will again bend away from the normal.
Hint: The direction of bending depends on the relative refractive indices of the lens and the surrounding medium.
Step 6: Emergent Rays
Draw the emergent rays after they pass through the lens. These rays will diverge as they exit the lens. Since the lens is concave and the refractive index of the lens is less than that of the surrounding medium, the rays will appear to diverge from a point on the principal axis.
Hint: The emergent rays will not converge; instead, they will spread out, indicating that the lens is acting as a diverging lens.
Step 7: Focal Point
Indicate the focal point on the right side of the lens. Since the lens is concave and the refractive index of the lens is less than that of the medium, the focal length will be positive, and the focus will be on the right side.
Hint: The focal point is where the rays appear to diverge from; it is a virtual focus for a concave lens.
Final Diagram
Combine all the elements into a final diagram showing the concave lens, incident rays, refracted rays at both surfaces, and the emergent rays along with the focal point.
Summary
The concave lens, when immersed in a medium with a higher refractive index, behaves as a diverging lens. The emergent rays diverge from a virtual focus on the right side of the lens.
We have a concave lens with a refractive index μ, and it is immersed in a medium with a refractive index μ1 where μ1>μ. A parallel beam of light is incident on the lens.
Draw a concave lens. The lens has two curved surfaces. Label the lens with its principal axis. The left side of the lens is where the light rays will be incident.
Draw two parallel lines representing the incident rays approaching the lens. These lines should be parallel to the principal axis of the lens.
When the parallel rays hit the first surface of the concave lens, they will refract. Since the lens has a lower refractive index than the surrounding medium, the rays will bend away from the normal.
After passing through the lens, the rays will hit the second surface. As they exit the lens into the medium with a higher refractive index, they will again bend away from the normal.
Draw the emergent rays after they pass through the lens. These rays will diverge as they exit the lens. Since the lens is concave and the refractive index of the lens is less than that of the surrounding medium, the rays will appear to diverge from a point on the principal axis.
Indicate the focal point on the right side of the lens. Since the lens is concave and the refractive index of the lens is less than that of the medium, the focal length will be positive, and the focus will be on the right side.
Combine all the elements into a final diagram showing the concave lens, incident rays, refracted rays at both surfaces, and the emergent rays along with the focal point.
The concave lens, when immersed in a medium with a higher refractive index, behaves as a diverging lens. The emergent rays diverge from a virtual focus on the right side of the lens.
Similar Questions
The refractive index of the material of a concave lens is n. It is immersed in a medium of refractive index n1. A paprallel beam of light is incident on the lens. Trace the path of emerged rays in each of the following cases :
(a) n1>n (b) n1<n ( c) n1=n.
View SolutionA transparent cube of side d, made of a material of refractive index μ2 , is immersed in a liquid of refractive index μ1(μ1<μ2). . A ray is incident on the face AV at an angle θ (shown in the figure). Total internal refraction takes place at point E on the face BC. Then must satisfy:
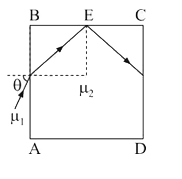
View Solution
Knowledge Check
A double convex lens, lens made of a material of refractive index μ1, is placed inside two liquids or refractive indices μ2 and μ3, as shown. μ2>μ1>μ3. A wide, parallel beam of light is incident on the lens from the left. The lens will give rise to
 Aa single convergent beamBtwo different convergent beamsCtwo different divergent beamsDa convergent and a divergent beam.
Aa single convergent beamBtwo different convergent beamsCtwo different divergent beamsDa convergent and a divergent beam.
A transparent cube of side d, made of a material of refractive index μ2 , is immersed in a liquid of refractive index μ1(μ1<μ2). . A ray is incident on the face AV at an angle θ (shown in the figure). Total internal refraction takes place at point E on the face BC. Then must satisfy:

View SolutionA clear transparent glass sphere (μ=1.5) of radius R is immersed in a liquid of refractive index 1.25. A parallel beam of light incident on it will converge to a point. The distance of this point from the center will be
View SolutionA thin bi-convex lens made out of a material of refractive index μ1 is place in a medium of refractive index μ2. A paraxial beam of light, parallel to the principal axis of the lens, is shown in the figure. Based on the ray diagram, we can conclude that

View SolutionWhen a lens of power P (in air) made of material of refractive index μ is immersed in liquid of refractive index μ0 Then the power of lens is:
View SolutionA lens made of material of Refractive index μ2 is surrounded by a medium of Refractive Index μ1. The focal length f is related as
View SolutionA lens made of material of Refractive index μ2 is surrounded by a medium of Refractive Index μ1. The focal length f is related as
View SolutionA bi-convex lens is cut from the middle as shown in figure. Refractive index of material of lens is 32. Now lens-1 (as shown in figure) is immersed in a liquid of refractive index μ0. By doing so it is observed that its focal length becomes equal to lens-2. What is the value of μ0 ?

View Solution
