A closed loop moves normal to a constant electric field between the plates of capacitor with plane of loop is normal to the field. When the loop is partially outside the plates of capacitor, the induced current in the loop
depends on speed of loop
depends on size of loop
depends of intensity of electric field
zero
The correct Answer is:D
To solve the problem of the induced current in a closed loop moving in a constant electric field between the plates of a capacitor, we can follow these steps:
1. Understand the Setup:
- We have a parallel plate capacitor that creates a constant electric field between its plates.
- A closed loop is placed such that its plane is normal (perpendicular) to the electric field and it moves through the electric field, with part of the loop being outside the plates of the capacitor.
2. Identify the Electric Field:
- The electric field (E) between the plates of a capacitor is uniform and constant. This means that the electric field does not change with time.
3. Calculate Electric Flux:
- The electric flux (Φ_E) through the loop is given by the formula:
ΦE=E⋅A
where A is the area of the loop that is within the electric field. Since the loop is partially outside the capacitor, only the area inside the plates contributes to the flux.
4. Determine Change in Flux:
- Since the electric field is constant and the area of the loop that is inside the electric field does not change (as the loop moves), the electric flux through the loop remains constant.
- Therefore, the rate of change of electric flux (dΦ_E/dt) is zero:
dΦEdt=0
5. Apply Faraday's Law of Induction:
- According to Faraday's law, the induced electromotive force (emf) in the loop is given by:
emf=−dΦEdt
- Since we found that dΦ_E/dt = 0, it follows that:
emf=0
6. Conclusion about Induced Current:
- The induced current (I) in the loop can be calculated using Ohm's law:
I=emfR
- Since the emf is zero, the induced current in the loop is also zero:
I=0
Final Answer:
The induced current in the loop is zero.
---
- We have a parallel plate capacitor that creates a constant electric field between its plates.
- A closed loop is placed such that its plane is normal (perpendicular) to the electric field and it moves through the electric field, with part of the loop being outside the plates of the capacitor.
- The electric field (E) between the plates of a capacitor is uniform and constant. This means that the electric field does not change with time.
- The electric flux (Φ_E) through the loop is given by the formula:
ΦE=E⋅A
where A is the area of the loop that is within the electric field. Since the loop is partially outside the capacitor, only the area inside the plates contributes to the flux.
- Since the electric field is constant and the area of the loop that is inside the electric field does not change (as the loop moves), the electric flux through the loop remains constant.
- Therefore, the rate of change of electric flux (dΦ_E/dt) is zero:
dΦEdt=0
- According to Faraday's law, the induced electromotive force (emf) in the loop is given by:
emf=−dΦEdt
- Since we found that dΦ_E/dt = 0, it follows that:
emf=0
- The induced current (I) in the loop can be calculated using Ohm's law:
I=emfR
- Since the emf is zero, the induced current in the loop is also zero:
I=0
The induced current in the loop is zero.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-IB18videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-II32videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Additional Exercise11videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)26videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II22videos
ELECTROMAGNETIC WAVES
Similar Questions
(a) A closed loop is held stationary in the magnetic field between the north and south poles of two permanent magnets held fixed. Can we hope to generate current in the loop by using very strong magnets?
(b) A closed loop moves normal to the constant electric field between the plates of a large capacitor. Is a current induced in the loop (i) when it is wholly inside the region between the capacitor plates (ii) when it is partially outside the plates of the capacitor? The electric field is normal to the plane of the loop.
(c) A rectangular loop and a circular loop are moving out of a uniform magnetic field region (Fig. 6.8) to a field-free region with a constant velocity v. In which loop do you expect the induced emf to be constant during the passage out of the field region? The field is normal to the loops.

(d) Predict the polarity of the capacitor in the situation described by Fig. 6.9.
 View Solution
View SolutionAn electron is moving near to a conducting loop then the induced current in the loop is-
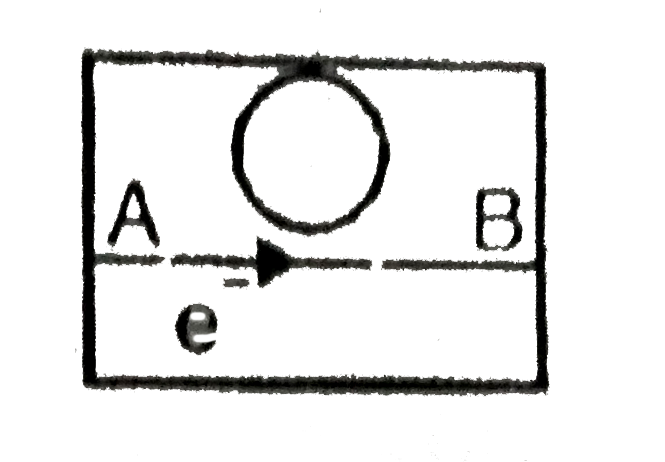 View Solution
View SolutionA metallic square loop ABCD is moving in its own plane with velocity v in a uniform magnetic field perpendicular to its plane as shown in the figure, Find
a) in which sides of the loop electric field is induced.
b) Net emf induced in the loop.
c) If one side .BC. is outside the field with remaining loop in the field and is being pulled on D with a constant velocity then induced current in the loop.
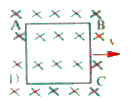 View Solution
View SolutionAssertion A conducting loop is rotated in a uniform magnetic field with constant angular velocity ω as shown in figure. At time t = 0, plane of the loop is perpendicular to the magnetic field. Induced emf produced in the loop is maximum when plane of loop is parallel to magnetic field.
Reason When plane of loop is parallel to magnetic field, then magnetic flux passing through the loop is zero.
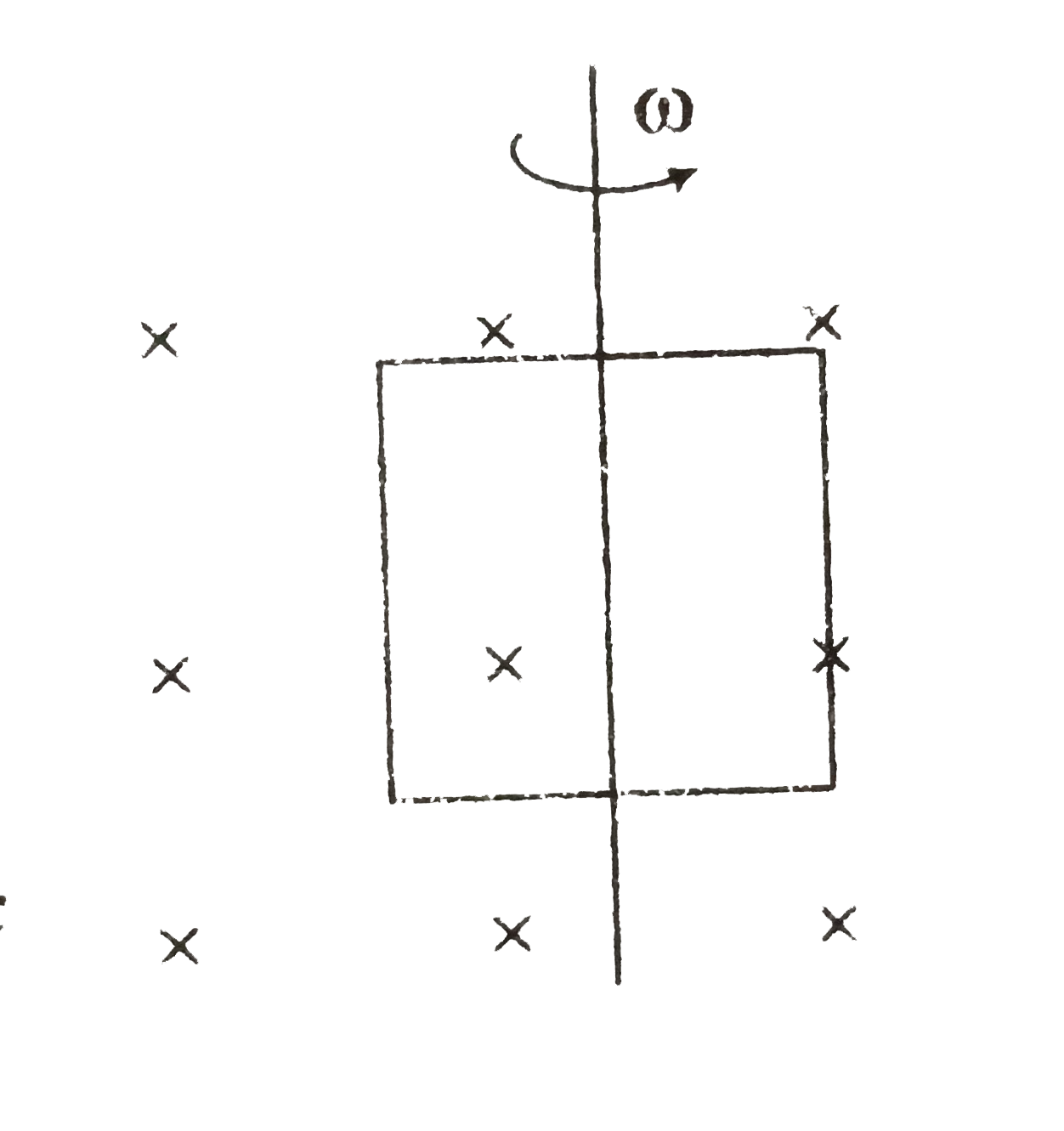 View Solution
View SolutionA superconducting loop of radius R has self inductance L.A uniform & constant magnetic field B is applied perpendicular to the plane of the loop. Initially current in this loop is zero. The loop is rotated about its diameter by 180∘.Find the current in the loop after rotation.
View SolutionA rectangular loop of wire with dimensions shown in figure is coplanar with a long wire carrying current 'I'. The distance between the wire and the left side of the loop is r. The loop is pulled to the right as indicated. What are the directions of the induced current in the loop and the magnetic forces on the left and right sides of the loop when the loop is pulled ?
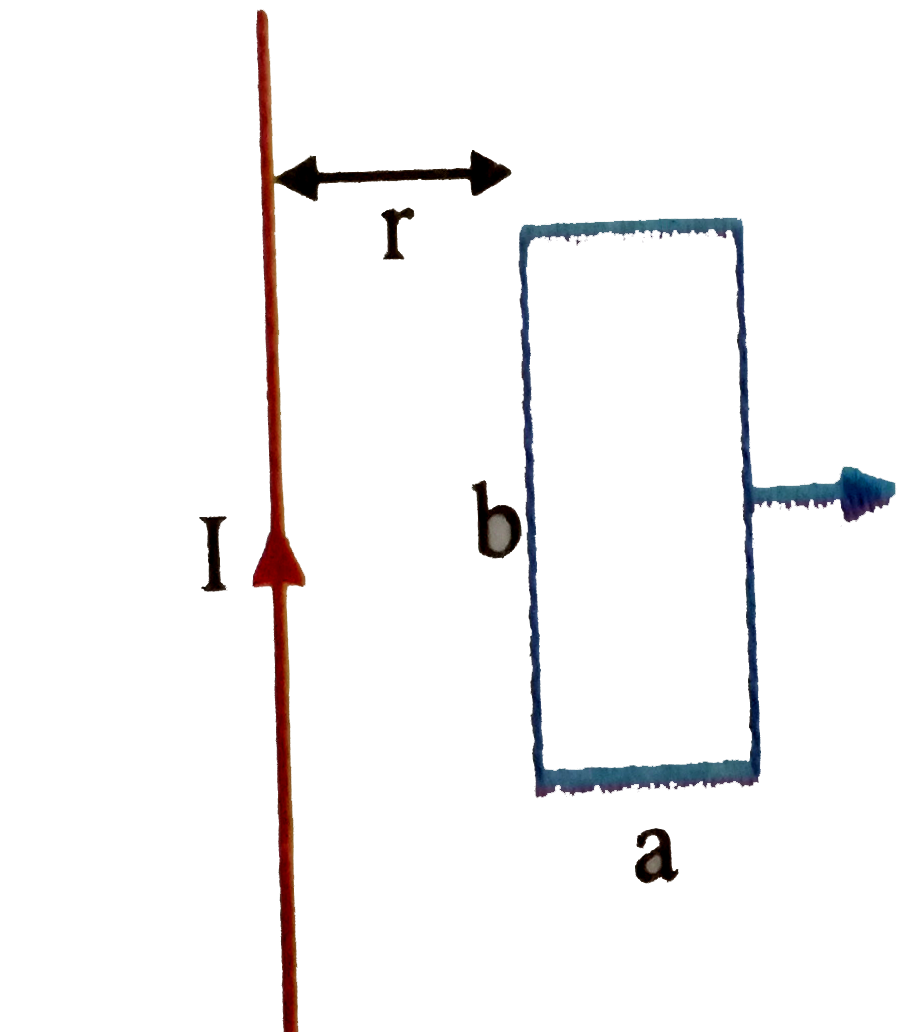 View Solution
View SolutionFig. shows planer loops of different shapes moving out of or into a region of magnetic field which is directed normal to the plane of the loops away from the reader. Determine the direction of induced current in each loop using Lenz's law. Check if you would obtain the same answers by considering magnetic force on the charge inside the moving loops.
 View Solution
View SolutionThe magnetic field B shown in is directed into the plane of the paper. ACDA is a semicircular conducting loop of radius r with the centre at O. The loop is now made ot rotate clockwise with a constant angular velocity ω about on axis passing through O and perpendicular to the plane of the paper. The resistance of the loop is R. Obtain an expression for the magnitude of the induced current in the loop. Plot a graph between the induced current i and ωt, for two periods of rotation.
 View Solution
View SolutionFigure shows planar loops of different shapes moving out of or into a region of a magnetic field which is directed normal to the plane of the loop away from the reader. Determine the direction of induced current in each loop using Lenz's law.
 View Solution
View SolutionA conducting square loop is placed in a magnetic field B with its plane perpendicular to the field. Now the sides of the loop start shrinking at a constant rate α. the induced emf in the loop at an instant when its side is a is
View Solution

