A closed orgain pipe of length l0 is resonating in 5th harmonic mode with rod clamped at two points l and 3l from one end. If the length of the rod is 4l and it is vibrating in first overtone. Find the length of the rod. [Velocity of sound in air =vs Young's modulus for the rod Y and density ρ]
![A closed orgain pipe of length l(0) is resonating in 5^(th) harmonic mode with rod clamped at two points l and 3l from one end. If the length of the rod is 4l and it is vibrating in first overtone. Find the length of the rod. [Velocity of sound in air =v(s) Young's modulus for the rod Y and density rho]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/FIT_JEE_PHY_GMP_ASS_E01_027_Q01.png)
The correct Answer is:125l0vs√yρ
For section AB
l=(2n−1)λ4,wheren=1,2,3,…
f1=vλ=(2n−1)v4l
For section BC
2l=mλ2,wherem=1,2,3,…
f2=vm4l
from (3)+(4)f1=f2
(2n−1)4l=mv4l
n=m+12
m=1,n=1 for fundamental , m=3,n=2
first overtone f2=mv4l=3v4l
Given that f=f2
5vs4l0=3v4l
l=3vl05vs
Therefore , length of the rod =4l=125l0vs√Yρ
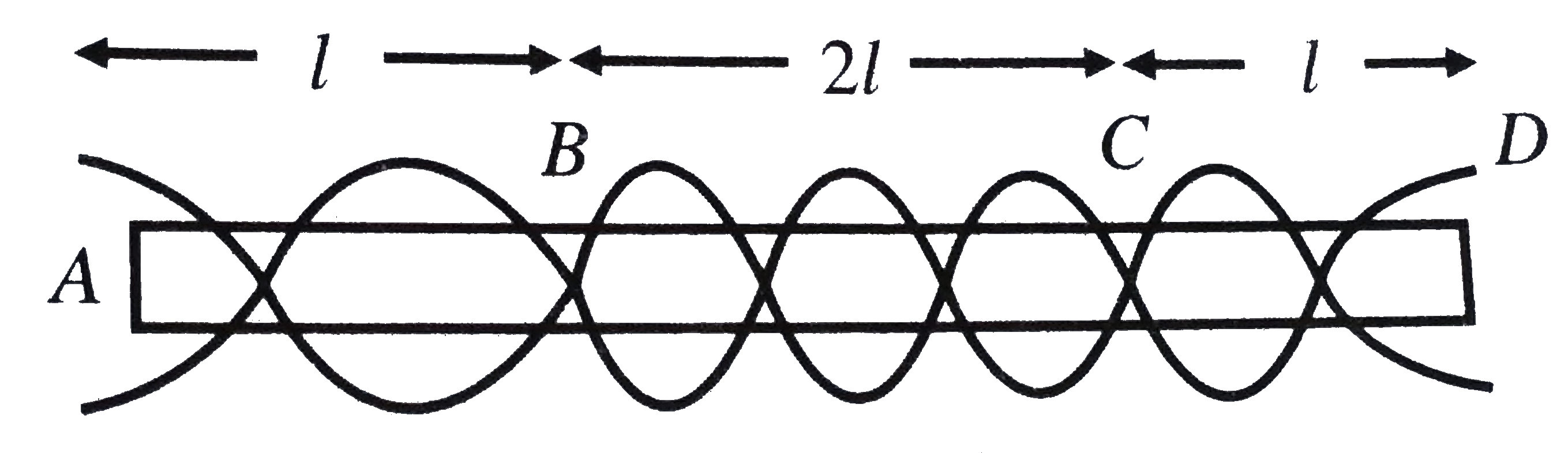
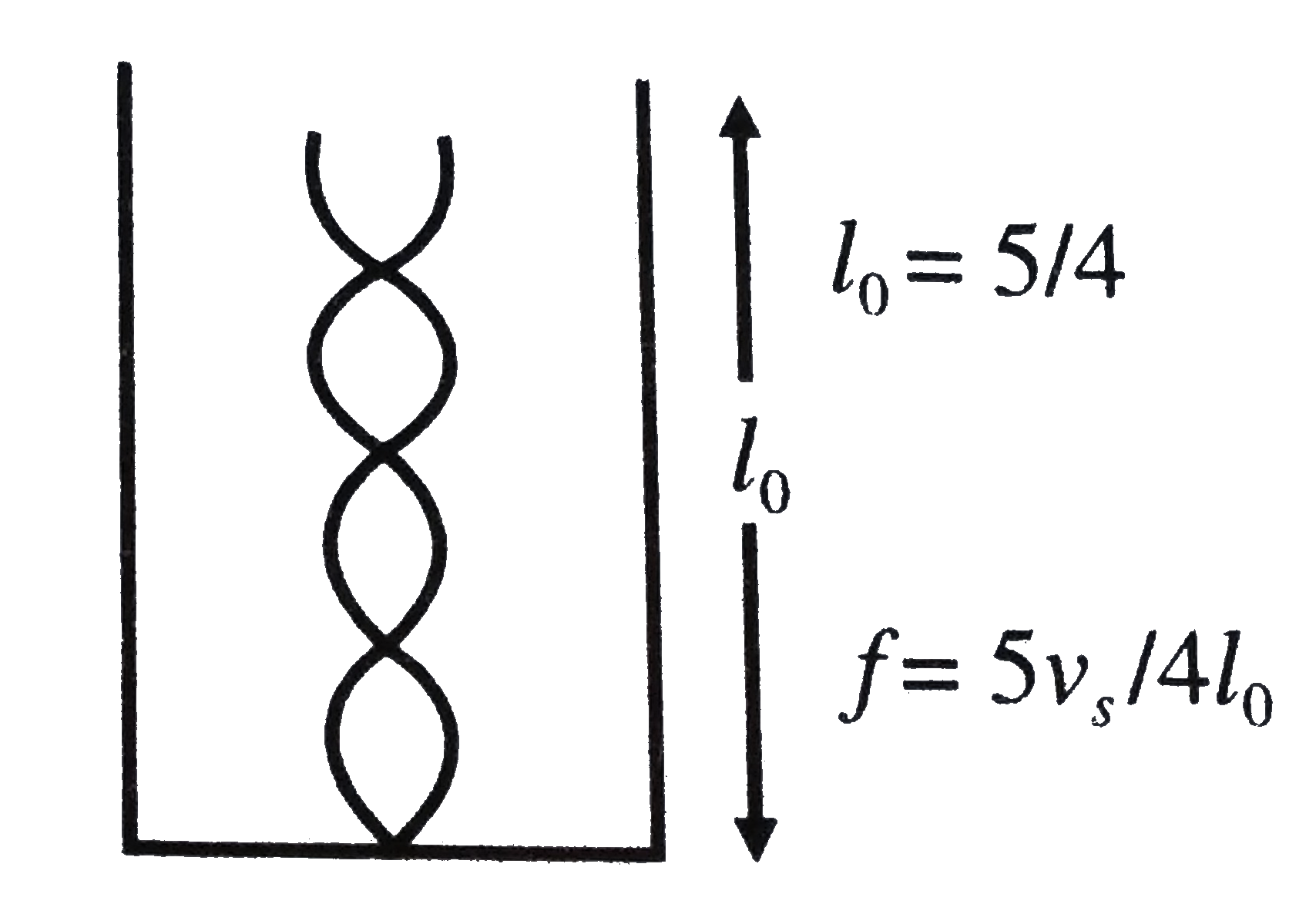
Topper's Solved these Questions
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Single Correct
144 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Multiple
26 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Exercise 7.2
32 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - 24
1 Videos
Similar Questions
A closed organ pipe of length L is in resonance with a tuning fork. If a hole is made in the pipe at a distance L4 from closed - end, it will be in resonance again, when:
View SolutionA rod of nickel of length l is clamped at its midpoint . The rod is stuck and vibrations are set up in the rod . Find the general expression for the frequency of the longitudinal vibrations of the rod . Young's modulus and density of the rod is Yandρ , respectively.
View SolutionA uniform rod of length L, has a mass per unit length λ and area of cross section A. The elongation in the rod is l due to its own weight, if it suspended form the celing of a room. The Young's modulus of the rod is
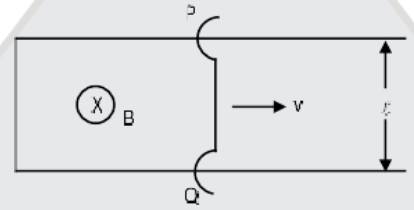
View SolutionA rod having length l and resistance R is moving with velocity v on a π shape conductor. Find the current in the rod.
View SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to the rod.

View SolutionA rod of length l is moving in a vertical plane (x−y) when the lowest point A of the rod is moved with a velocity v. find the a angular velocity of the rod and b velocity of the end B.

View SolutionA rod AB of mass M and length L is shown in figure. End A of rod is hinged and end B is lying on the ground. Find the Normal reaction by ground on the rod

View SolutionFind the electric field at a point P on the perpendicular bisector of a uniformly charged rod. The length of the rod is L, the charge on it is Q and the distance of P from the centre of the rod is a.
View SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to tke rod.

View SolutionA metal rod of length L is clamped at a distance L/4 from one end. It is set into longitudinal vibrations . The wavlength for fundamental mode of vibrations will be
View Solution
