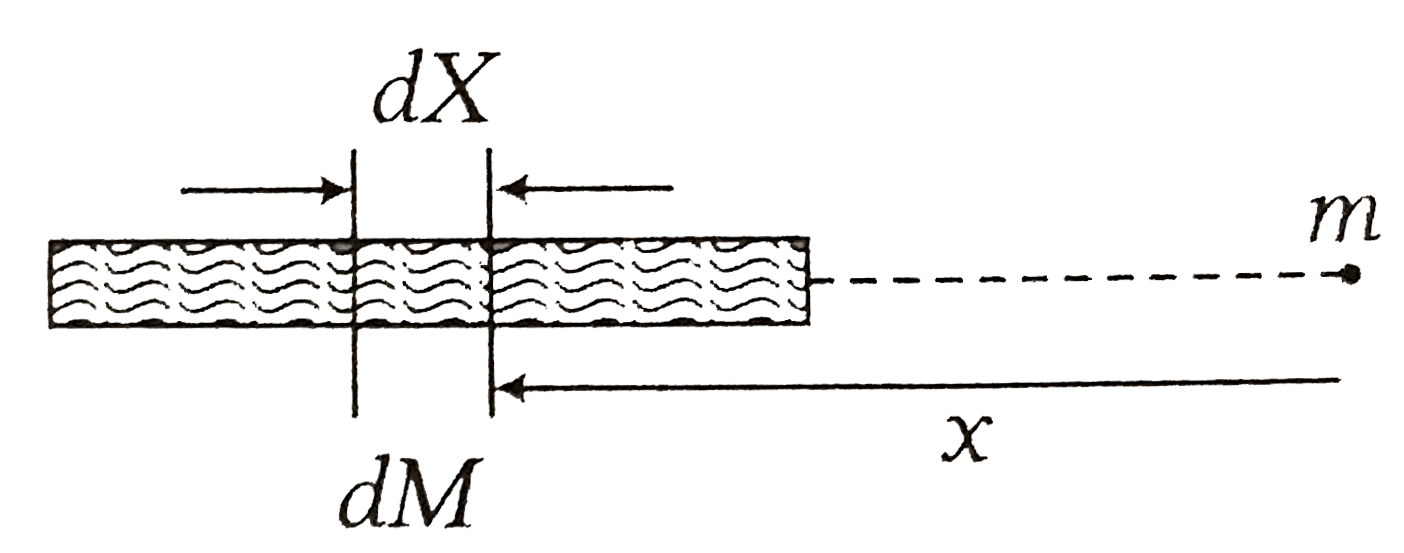
A mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to the rod. 
4GMm(a+l)2
4GmM4a2−l2
GMma2
GmM2(l+a)2
The correct Answer is:B
dF=GmdMx2
∴F=∫x=a+1x=adF
=∫a+la−l/2G.m(Ml.dx)x2=4GmM4a2−l2
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (B) Chapter Exercises
31 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.6
20 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
A mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to tke rod.

View SolutionA particle of mass m is situated at a distance d from one end of a rod of mass M and length L as shown in diagram. Find the magnitude of the gravitational force between them

View SolutionTwo uniform solid of masses m1 and m2 and radii r1 and r2 respectively, are connected at the ends of a uniform rod of length l and mass m. Find the moment of inertia of the system about an axis perpendicular to the rod and passing through a point at a distance of a from the centre of mass of the rod as shown in figure.

View SolutionA semicircular wire has a length L and mass M. A particle of mass m is placed at the centre of the circle. Find the gravitational attraction on the particle due to the wire.
View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is

View SolutionCalculate the moment of inertia of a uniform rod of mass M and length l about an axis passing through an end and perpendicular to the rod. The rod can be divided into a number of mass elements along the length of the rod.
View SolutionThe density of a thin rod of length l varies with the distance x from one end as ρ=ρ0x2l2. Find the position of centre of mass of rod.
View SolutionIf a street light of mass M is suspended from the end of a uniform rod of length L in different possible patterns as shown in figure, then:
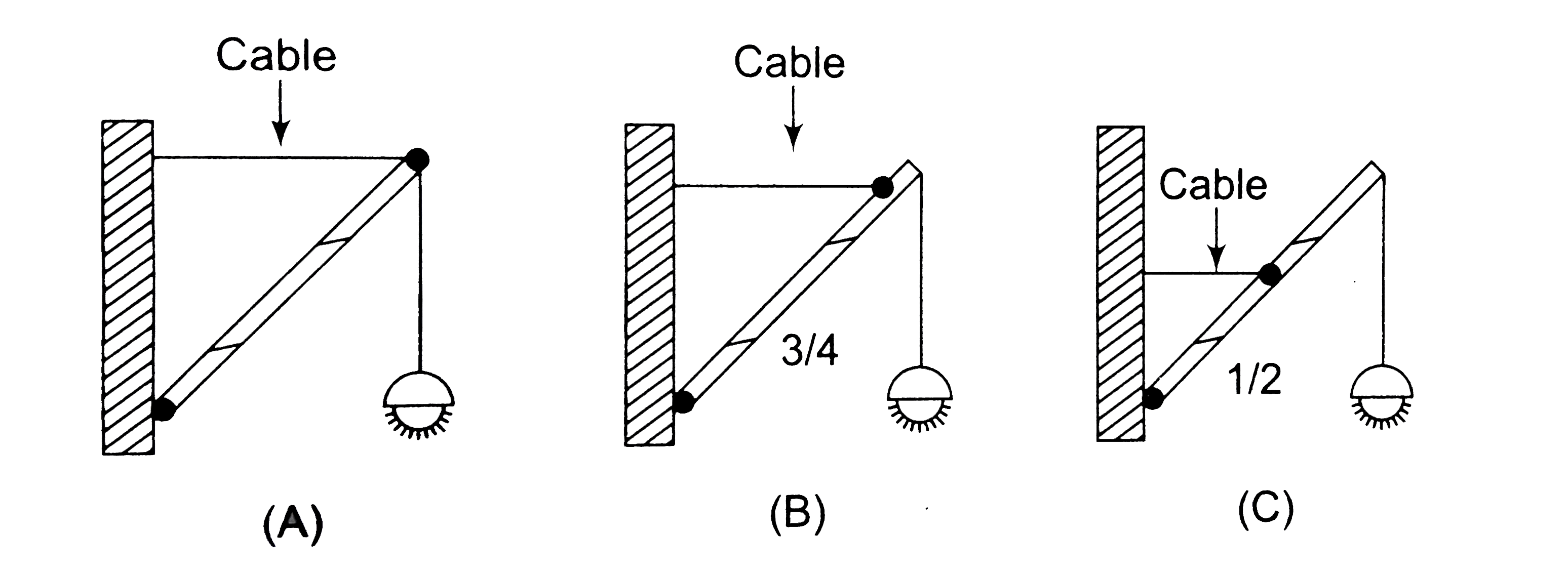
View SolutionThe moment of inertia of a uniform thin rod of length L and mass M about an axis passing through a point at a distance of L/3 from one of its ends and perpendicular to the rod is
View Solution
